Website owner:  James Miller

Cauchy’s integral formulas, Cauchy’s inequality, Liouville’s theorem, Gauss’ mean value theorem, maximum modulus theorem, minimum modulus theorem

Cauchy’s integral formulas

Theorem 1. If f(z) is analytic inside and on the boundary C of a simply-connected region R and a is any point inside C then

where C is traversed in the positive direction. Proof

In addition the n-th derivative of f(z) at z = a is given by

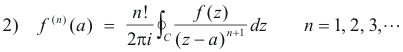
where C is traversed in the positive direction. Proof

Formula 1) above can be considered a special case of 2) with n = 0 if we define 0! = 1.

Formulas 1) and 2) above are known as Cauchy’s integral formulas.

It can be shown that Cauchy’s integral formulas are valid not only for simply-connected regions but also for multiply-connected ones. Proof

Theorem 2. If a function f(z) is analytic inside and on the boundary C of a simply-connected region R, then all its higher order derivatives exist and are analytic in R.

Cauchy’s integration formulas reveal the remarkable fact that if a function is analytic within a simply-connected region R and C is any simple closed curve within R then the values of the function and all of its derivatives, at all points within C, are completely determined by the values of the function along C (i.e. the values of a function and all its derivatives are fixed by the values of the function along C). In fact, it can be shown that if in a region R two analytic functions are given that agree on some curve C within R, then they agree on the entire region. If we know the values of an analytic function on some segment of a curve in a region, then the values of the function are uniquely determined everywhere in the region. Thus we see that the values of an analytic function in different parts of the complex plane are closely connected to one another. To appreciate the significance of this we need remember that the general definition of a function of a complex variable allows any correspondence between the values of the argument and the values of the function i.e. the function may assign any value whatever to any point z. Such a definition gives no possibility of determining values of a function at some point from its values in another part of the plane. We thus see that the single requirement of differentiability of a function of a complex variable is so strong that it forces a connection between values of the function at different places.

Some important theorems

Following are some important theorems that are consequences of Cauchy’s integral formulas.

1. Cauchy’s inequality. If f(z) is analytic inside and on a circle C of radius r and center at a, then

where M is a constant such that |f(z)| < M on C, i.e. M is an upper bound of |f(z)| on C.    Proof

2. Liouville’s theorem. If f(z) is analytic in the entire complex plane and is bounded (i.e. |f(z)| < M for some constant M) then f(x) must be a constant. Proof

3. Fundamental theorem of algebra. Every polynomial equation of degree n 1 with complex coefficients has at least one root. Proof

4. Gauss’ mean value theorem. Let f(z) be analytic inside and on a circle C of radius r and center at a. Then f(a) is the mean of the values of f(z) on C, i.e.

Proof

5. Maximum modulus theorem. Let f(z) be analytic on a closed region R with boundary C and let M be the maximum value assumed by |f(z)| in R. Then, if f(z) is not identically equal to a constant, the maximum value M of |f(z)| occurs on the boundary C. In addition, at all points on the interior of R, |f(z)| < M.

In other words, a function that is analytic in a region assumes its maximum value on the boundary of the region and not in the interior providing it is not a constant.

6. Minimum modulus theorem. Let f(z) be analytic on a closed region R with boundary C and let be the minimum value assumed by |f(z)| in R. Then, providing f(z) 0 throughout R, the minimum value of |f(z)| occurs on the boundary C. In addition, at all points on the interior of R, |f(z)| > .

In other words, a function that is analytic in a region assumes its minimum value on the boundary of the region and not in the interior providing it is not identically zero.

References

  Mathematics, Its Content, Methods and Meaning

  James and James. Mathematics Dictionary

  Spiegel. Complex Variables (Schaum)

  Wylie. Advanced Engineering Mathematics

  Hauser. Complex Variables with Physical Applications.