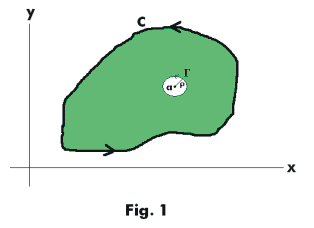
Prove: If f(z) is analytic inside and on the boundary C of a simply-connected region R and a is any point inside C then

Proof. The function f(z)/(z-a) is analytic inside and on C except at the point z = a.. Construct a circle Γ of radius ρ at point a as shown in Fig. 1. Then by the principle of the deformation of contours

The right member of 1) can be written as

We compute the second term first. On the circle Γ

3)        z = a + ρ(cos θ + i sinθ) .

Noting that a and ρ are constant, we get

4)        dz = ρ(-sin θ + i cos θ)dθ = iρ(cos θ + i sin θ)dθ

From 3) we get

            z - a = ρ(cos θ + i sinθ)

and the second term of 2) becomes

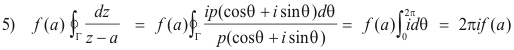
Equation 2) then becomes

In the above equation let us take limits as ρ 0. The left side and the first term of the right side will remain unchanged. We will show that the limit of the second term is equal to zero. In order to show that it approaches zero as ρ 0 note that

This means that the quantity [f(z)- f(a)]/(z-a) is bounded i.e.

Applying property 5 of the integral which states that

where |f(z)| M ( i.e. M is an upper bound of |f(z)| on C) and L is the length of C, we get

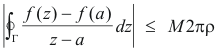
which approaches zero as ρ 0.

Equation 6) then becomes

or

References

  Mathematics, Its Content, Methods and Meaning. Vol II

  Spiegel. Complex Variables (Schaum)

  Wylie. Advanced Engineering Mathematics