Prove. If f(z) is analytic inside and on the boundary C of a multiply-connected region R and a is any point inside C then

where C is traversed in the positive direction.

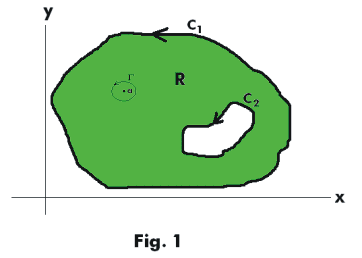
Proof. We will present a proof for the multiply-connected region R shown in Fig. 1 bounded by the curves C₁ and C₂. Extensions to other multiply-connected regions are easily made.

Construct a circle Γ with its center at any point a in R and a radius such that the circle lies entirely within R. Let the direction of curves C₁ and Γ be counterclockwise as shown in the figure. Let R' consist of the set of points in R that are exterior to Γ. We note that the function f(z)/(z-a) has a singularity at point a. Because point a lies outside R', the function f(z)/(z-a) is analytic inside and on the boundary of R'. We now apply Cauchy’s theorem for multiply-connected regions to the function f(z)/(z-a) over the boundary of R' to get

and multiply by 1/2πi to give

Now by Cauchy’s integral formula for simply-connected regions we have

Substituting 3) into 2) we obtain

If we now let C denote the total boundary of R, traversed properly so that one moving along C always has the region to his left, we can write 4) as

In a similar manner we can show that the other Cauchy integral formulas

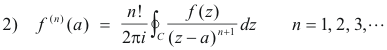
hold for multiply-connected regions.

References

  Spiegel. Complex Variables (Schaum)