Prove: Fundamental theorem of algebra. Every polynomial equation

            P(z) = a₀zⁿ + a₁z^{n -1} + ... + a_n-1z + a_n = 0

 of degree n 1 with complex coefficients has at least one root.

Proof. If we assume that P(z) has no root, then the function f(z) = 1/P(z) is analytic for all z (i.e. it possesses no singular points). In addition,

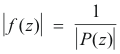
is bounded. Why? Because |f(z)| 0 as |z| . Then by Liouville’s theorem we conclude that f(z) must be a constant. And if f(z) is a constant, so is P(z). But we know that P(z) is not a constant. Thus we have been led to a contradiction and conclude that P(z) = 0 must have at least one root.