Website owner: James Miller
Real and virtual images. Image formation by lenses, plane mirrors, concave and convex spherical mirrors. Graphical methods for locating images. Thin lens equation. Lensmaker’s equation.

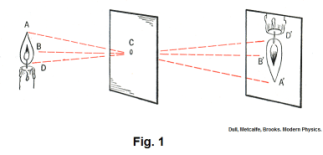
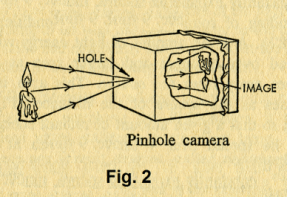
Real and virtual images. In a dark room one can form an image of a candle flame on a white screen by letting the rays from the candle pass through a small opening. See Fig. 1. This idea is used in the pinhole camera. The pinhole camera is simply a light-proof box with a tiny pinhole in the front and photographic film stretched across the rear wall. See Fig. 2. One uncovers the pinhole for a minute or so, then covers it back up, to take a picture. If it is held steady, it can take a good picture. If one replaces the pinhole with a lens, the intensity of the incident light is increased and a sharp image can be recorded in a fraction of a second. The image formed by a pinhole or a lens is formed by incident rays of light on a surface and stands in contrast to another kind of image — the kind of image formed by a mirror. The image formed by a mirror is not real, it is an illusion formed by the way the light reflects off the mirror. The image seen in a mirror looks three dimensional and real but we know there is nothing where the image appears to be. An image such as that formed by a pinhole or lens is called a real image. An image such as that formed by a mirror is called a virtual image.
Real images. A real image is an image formed by actual rays of light. Real images are always inverted, and they may be either larger or smaller than the object.
Virtual images. An image, such as that seen in a mirror, in which the rays of light appear to be emanating from some object that isn’t there is called a virtual image. Virtual images are always erect. They, also, may be either larger or smaller than the object.
Mirrors. A mirror is a highly reflecting smooth surface that can be used to form an image. By making the surface of highly polished metal, or by applying a thin metallic coat to a polished surface, the fraction of light reflected can be made nearly 100%. The most commonly used mirrors consist of flat pieces of plate glass that have been silvered on one side.
Convex and concave spherical mirrors. A convex spherical mirror consists of a mirrored outer surface of a section of a sphere. A concave spherical mirror consists of a mirrored inner surface of a section of a hollow sphere. A convex mirror is curved outward toward the observer; a concave mirror is

curved inward away from the observer. Se Fig. 3.
Image formation by plane mirrors.
Theorem. The image formed by a plane mirror is erect, virtual, the same size as the object, and is located as far behind the mirror as the object is in front of it. Because the image is formed by a direct projection through the mirror, it is reversed (e.g. your right eye appears as the left eye in your image, etc.).
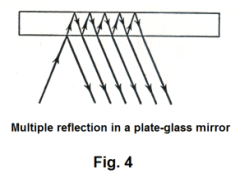
Multiple reflection. Just as sound waves can bound back and forth between parallel walls creating echos and re-echos, light can reflect back and forth between parallel mirrors creating multiple images. The image formed in one mirror can act as an object to form an image in another mirror. Fig. 4 shows multiple reflection in a thick plate-glass mirror due to reflection from both front and rear surfaces. Such a phenomenon can produce an annoying series of images of a bright object. In multiple reflections such as this, some light is absorbed at each reflection and, as a consequence, each succeeding image is fainter than the one producing it.
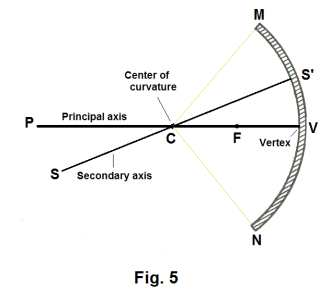
Terms used with curved mirrors. See Fig. 5.
Center of curvature, C. The center of the sphere of which the mirror forms a part.
Aperture. The angular portion, MCN, of the sphere that is included by the mirror.
Vertex, V. The center of the mirror.
Principal axis. The line passing through the center of curvature, C, and the vertex, V.

Secondary axis. Any line drawn through the center of curvature, C, intersecting the mirror, other than the principal axis.
Normal to the surface. The normal to the mirror surface at a particular point is given by the direction of the radius to that point.
Focusing of light rays by a concave spherical mirror. We wish now to consider how light rays are focused by a concave spherical mirror such as the one shown in Fig. 6. We first want to consider how parallel rays coming in from an object at infinite distance (such as the sun) focus. Do all the rays converge at the same point? The answer to that question is, “No.” Just how then do they converge?
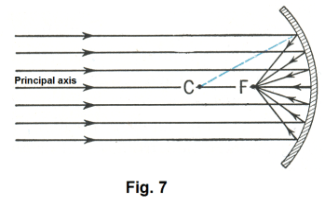
In Fig. 7 is shown an arbitrary slice through the principal axis showing parallel rays coming in and reflecting off the mirror. In Fig. 8 is shown a single ray coming in. It comes in and is reflected from the mirror at point A in accordance with the laws of reflection and then passes through the principal axis at point B. We are going to compute the location at which it crosses the axis. We will find that the location at which it crosses the axis depends on the angle θ.
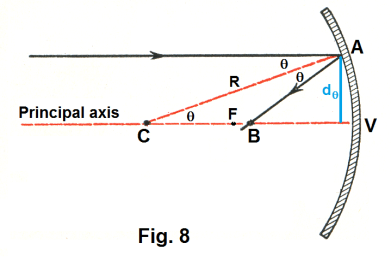
We have stated that the reflected ray will pass through the principal axis. Why must it pass through the principal axis? Because the laws of reflection state that the reflected ray must lie in the plane of the incident ray and the normal --- and the normal at point A passes through the center of curvature C.
Thus the reflected ray must remain in the plane containing the incident ray, the point C,
Angle θ (degrees) |
dVB (cm) |
dBF (cm) |
0.01o |
49.9999992 cm |
0.0000008 cm |
0.05 |
49.9999809 |
0.0000191 |
0.1 |
49.9999238 |
0.0000762 |
0.5 |
49.9980960 |
0.0019040 |
1 |
49.9923836 |
0.0076164 |
2 |
49.9695227 |
0.0304773 |
5 |
49.8090081 |
0.1909919 |
7 |
49.6245087 |
0.3754913 |
10 |
49.2286694 |
0.7713306 |
12 |
48.8829702 |
1.1170297 |
15 |
48.2361909 |
1.7638091 |
20 |
46.7911113 |
3.2088887 |
25 |
44.8311040 |
5.1688960 |
Table 1
and the axis passing through C that is parallel to it (the incoming ray) --- which for incoming rays parallel to the principal axis is the principal axis.
We specify the location of B by its distance from the vertex V, calling that distance dVB. In order to compute dVB, we first compute the length of the line segment CB which we denote by lCB. The formula is
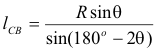
where R is the radius of curvature. The distance dVB is then given by
dVB = R - lCD
Column 2 of Table 1 shows the computed values of dVB for various values of the angle θ for a concave spherical mirror with a radius of curvature of R = 100 cm. From this data one can see that for small angles the value of dVB approaches (but never reaches) the value of 50 cm, which is the point midway between the vertex V and the center of curvature C. This point midway between the vertex and the center of curvature is called the principal focus. We thus see that for small angles of θ, the rays of light pass through the principal axis very close to the principal focus. Column 2 of the table shows values of dBF, which is the distance between the point B of intersection and the principal focus. We see that for small angles these numbers are very small, but when we get to angles of over 12o they exceed 1 cm and at 25o they are over 5 cm.
Referring to Fig. 8, the distance of an incoming ray from the principal axis is shown in blue as dθ, where dθ = Rsinθ. The set of all incoming rays reflecting at an angle θ and intersecting the principal axis at point B correspond to the surface of a cylinder centered on the principal axis with a radius dθ.
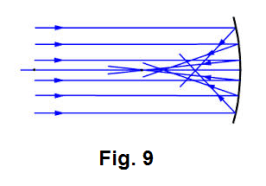
So what kind of picture does the above discussion give us? The reflected rays from incoming rays that are close to the principal axis (and the center of the mirror) and reflecting at small angles will pass very near the principal focus (for practical purposes, we can say that they pass through it). The reflected rays from incoming rays that are further out from the principal axis and reflecting at larger angles will pass further away from the principal focus. One has the effect shown in Fig. 9. It is called spherical aberration. The effect is a blurring effect on images.
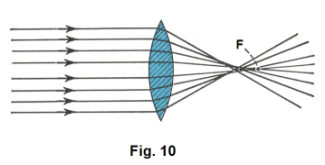
We have been talking about the focusing of rays with a concave spherical mirror as a specific example, but the discussion also applies to convex spherical mirrors and lenses. Fig. 10 illustrates the same phenomenon with a lens. The incoming parallel rays are bent by the lens and go approximately through the principal focus, and the ones close to the principal axis do go through it for all practical purposes, but those further out towards the outer fringes of the lens deviate substantially from it.
Def. Focal point. A point at which rays meet.
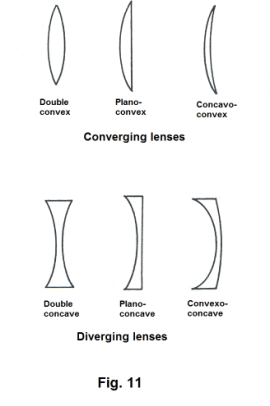
Lenses. A lens consists of a transparent material bounded by two curved surfaces, or a curved surface and a plane surface, both of which are smooth and highly polished. There are two types of lenses — converging and diverging. Converging lenses are thicker in the middle than at the edge and cause incoming parallel rays of light to converge to a point as shown in Fig. 10. Diverging lenses cause incoming parallel rays to diverge on passing through the lens. The main kinds of converging and diverging lenses are shown in Fig. 11. Different types are used for different purposes. For example, a concavo-convex lens is used to correct farsightedness and a convexo-concave lens is used to correct nearsightedness.
Terms used with lenses. See Fig. 12.
Centers of curvature, C and C'. There are two centers of curvature, C and C'. They are the centers of the intersecting spheres that form the left and right surfaces of the lens.
Principal axis. The line passing through the two centers of curvature, C and C'.
Optical center. The point at or near the geometric center of the lens where light passes straight through and doesn’t deviate.
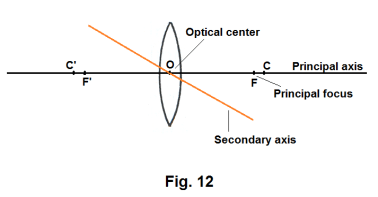
Secondary axis. Any line passing through the optical center other than the principal axis.
Principal focus. The point where incoming light rays that are parallel to, and very close to, the principal axis focus. Its location depends on the index of refraction of the lens. With a double convex lens of crown glass, the principal foci and the centers of curvature almost coincide.
Focal length. The distance of the principal focus from the optical center.
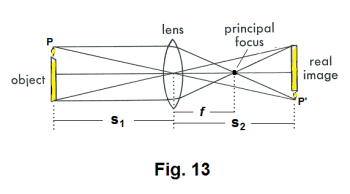
Image formation by a lens. Fig. 13 shows a lens creating a real image of a candle. The image created is inverted. If a lens with a focal length f is held at a distance s1 > f from a candle, a real image is formed on the opposite side of the lens, at a distance s2 from the lens, where s1 and s2 are related through the equation
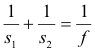
The rays from a particular point P on the candle will pass through the lens and converge to form an image P' of P at a point located at a distance s2 on the other side of the lens. A focused image of the candle will appear on a white screen that is held at a distance s2 from the lens. We now wish to make an observation. We know experimentally that a lens will form a real image of an object in the manner that we have just shown. This simple fact implies the following: A ray emanating from a point P on an object that strikes anywhere on the object side of the lens will be so bent by the lens as to cause it to pass through its image P' or close to it (those passing near the center of the lens will pass through or very near P' and those striking the lens near its outer rim will pass further from P'). If this fact were not true no image would be formed.
Graphical methods for locating images formed by thin lenses. The position and size of the image of an object can be found by a simple graphical technique. The technique employs the following three rays:
Ray 1. See Fig. 14 (a) and (b). An incoming ray moving parallel to the principal axis will be bent by a converging lens so as to pass through the focal point on the opposite side as is shown for Ray 1 in Fig. 14(a). In the case of a diverging lens, the ray is bent in such a way that its extension passes through the object-side focal point as is shown for Ray 1 of Fig. 14(b).
Ray 2. Rays passing through the center of the lens undergo no deviation as shown by Ray 2 of Fig. 14 (a) and (b).
Ray 3. Rays passing through an object-side focal point are bent by a converging lens to move parallel to the principal axis as shown by Ray 3 of Fig. 14(a). In the case of a diverging lens, a ray that is initially pointed toward the focal point on the opposite side of the lens will be bent by the lens so as to move parallel to the principal axis as is shown by Ray 3 in Fig. 14(b).
Rays 1, 2, and 3 of Fig. 14 represent three kinds of rays that can be easily drawn to locate image points. Any two of these rays drawn from an object point Q will intersect in image space to determine an image point Q'.
Type, size and location of images formed by a converging lens. The type of image produced by a converging lens depends on the distance of the object from the lens.
Case 1. Object is at a finite distance of more than 2f (two focal lengths) from the lens. The image is real, inverted, reduced, and located at a distance of between f and 2f on the other side of the lens. See Fig. 15, (1).

Applications: Lenses of the eye, camera, telescope.
Case 2. Object at a distance of 2f from the lens. The image is real, inverted, the same size as the object, and located at a distance of 2f from the opposite side of the lens. See Fig. 15, (2).
Applications: Used to invert an image without changing its size, as in a field telescope.
Case 3. Object is between one and two f from the lens. The image is real, inverted, enlarged, and located more than 2f from the opposite side of the lens. See Fig. 15, (3).
Applications: Compound microscope, slide projector, motion picture projector.
Case 4. Object is less than f from the lens. Image is virtual, erect, enlarged, and located on the same side of the lens as the object. See Fig. 15, (4).
Applications: Magnifying glass; eyepiece lens of microscopes, binoculars, and telescopes.
Note. (1) If the object is at infinity, the image is a point at the principal focus. (2) If the object is at the principal focus, no image is formed.
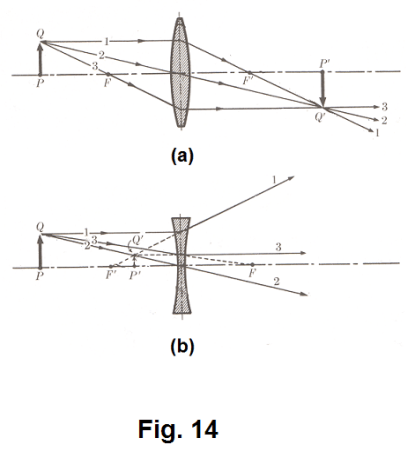
Images formed by diverging lenses. The only kind of image that can be formed by a diverging lens is virtual, erect, and reduced in size. See Fig. 16.
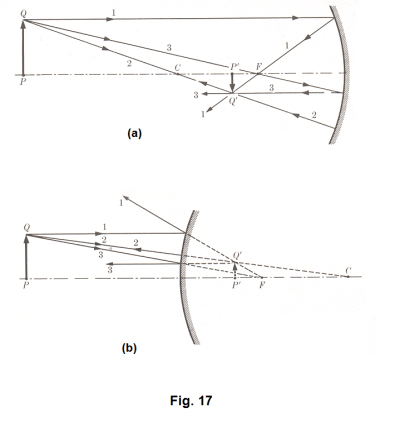
Image formation by spherical mirrors. Real and virtual images are formed by concave and convex spherical mirrors, just as they are by lenses. A concave mirror will form a real image of a burning candle just as a lens does. An important difference between spherical mirrors and lenses is that the focal length f of a spherical mirror is R/2 while the focal length of a lens is usually approximately R.
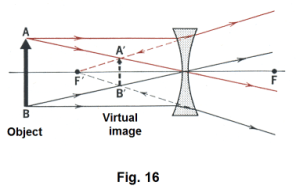
Graphical methods for locating images formed by spherical mirrors. The position and size of the image formed by a spherical mirror is found by employing the following three rays:
Ray 1. A ray parallel to the principal axis. After reflection, this ray passes through the focal point of a concave mirror. See Fig. 17 (a), Ray 1. In a convex mirror, it reflects in such a way that it appears to come from the focal point of the mirror. See Fig. 17 (b).
Ray 2. A ray passing through, or in the direction of, the center of curvature C. This ray intersects the surface normally and is reflected back along its original path. See Fig. 17 (a) and (b), Ray 2
Ray 3. A ray passing through, or in the direction of, the principal focus. This ray is reflected parallel to the principal axis. See Fig. 17 (a) and (b), Ray 3.
Type, size and location of images formed by a concave spherical mirror. The type of image produced by a concave spherical mirror depends on the distance of the object from the mirror.
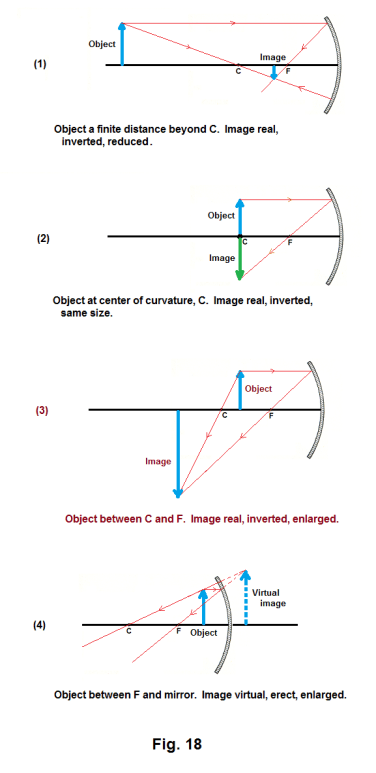
Case 1. Object is at a finite distance beyond the center of curvature, C. The image is real, inverted, reduced, and located between C and principal focus, F. See Fig. 18, (1).
Case 2. Object is at the center of curvature, C. The image is real, inverted, the same size, and located at C. See Fig. 18, (2).
Case 3. Object is between C and F. The image is real, inverted, enlarged, and located beyond C. See Fig. 18, (3).
Case 4. Object is between F and mirror. The image is virtual, erect, enlarged, and located behind the mirror. See Fig. 18, (4).
Note. (1) If the object is at infinity, the image is a point at the principal focus. (2) If the object is at the principal focus, no image is formed.
Images formed by convex mirrors. All images formed by convex mirrors are virtual, erect, smaller than the object, and located between the mirror and the principal focus. See Fig. 19.
Lens and mirror equations. The following two equations apply to all thin lenses, converging or diverging, and also to spherical mirrors (concave or convex):
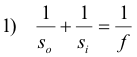
where so represents the object distance, si the image distance, and f the focal length.
Derivation for a concave mirror
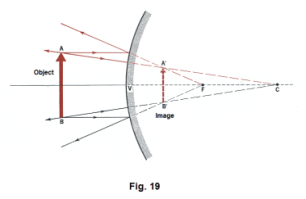
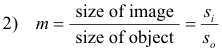
where m is the linear magnification. In the case of lenses, equation 1) is known as the thin lenses equation. ____________________________________________________________________________
Conventions. In these last two equations 1) and 2), and in the equations and discussion that follows, the following conventions are assumed:
I Lenses and spherical refracting surfaces.
1. Light is assumed to travel from left to right, come to the lens (or refracting surface) from the left.
2. The object distance so is positive when the object is to the left of the lens, negative when it is on the right.
3. The image distance si is positive when the image is on the right of the lens, negative when it is on the left.
4. Radii of curvature R are considered positive if the center of curvature lies at the right of the surface. Thus the radius of curvature R is positive for a convex surface and negative for a concave surface.
5. The focal length f is positive for a converging lens, negative for a diverging lens.
II Concave and convex spherical mirrors.
1. Light is assumed to travel from left to right, come to the mirror from the left.
2. The object distance so is positive when the object is to the left of the mirror, negative when it is on the right.
3. The image distance si is positive when the image is on the left of the mirror, negative when it is on the right.
4. Radii of curvature R are considered positive if the center of curvature lies at the left of the mirror. Thus the radius of curvature R is positive for a concave mirror, negative for a convex mirror.
5. The focal length f is positive for a concave mirror, negative for a convex mirror.
Note. Some authors use the same convention for mirrors as for lenses but this results in formula 1) being different for mirrors.
____________________________________________________________________________
Lensmaker’s equation. The following is known as the lensmaker’s equation:
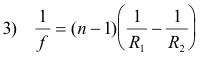
where
f = focal length of lens
n = refractive index of the lens material
R1 and R2 = radii of curvature of the two lens surfaces
Theorem 1. When two thin lenses having focal lengths f1 and f2 are in contact, the focal length of the combination is given by the equation
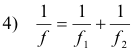
____________________________________________________________________
Refraction at a spherical surface.
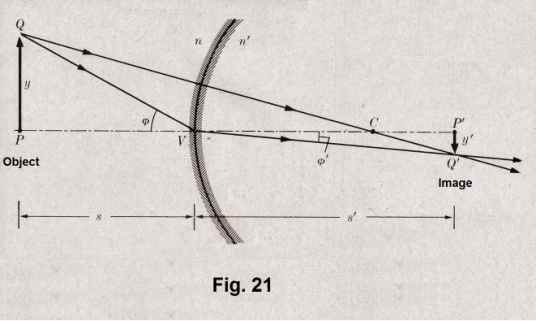
Theorem 2. Two transparent medium, Medium 1 and Medium 2, are separated by an interfacial spherical surface that has its center at point C in Medium 2 with a radius R. See Fig. 20. The index of refraction of Medium 1 is n and the index of refraction of Medium 2 is n'. A point P in Medium 1 located at a distance s from the surface is imaged into a point P' in Medium 2. P' is located on the axis through P and C and intersecting the surface at vertex V, at a distance s' from V.
We also make the following assumption: We assume that we are dealing with rays that are very close to the principal axis and make very small angles with the principal axis (angles of less than 10o), resulting in very small angles of incidence. Such rays are called paraxial rays. Thus we assume that the angles we are dealing with are small enough that we can approximate them by their sines and tangents (for very small angles, sin θ ≅ θ and tan θ ≅ θ).
Given the above conditions, the following relationship holds between the variables n, n', s, s', and R:
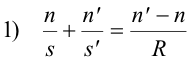
Also, the magnification factor m for the ratio of image size to object size is given by

Proof. Referring to Fig. 20, the ray PV, incident normally to the surface, passes to point P' without deviation. An arbitrarily chosen ray PB makes an angle u with the axis, is incident on the interfacial surface at B at an angle of incidence φ, is refracted at an angle of refraction φ', and then passes through point P' as shown in the figure. From triangles PBC and P'BC we have
3) φ = θ + u
4) θ = u' + φ'
(Reason? The exterior angle of a triangle is equal to the sum of the interior angles). Applying Snell’s law to the refraction at B, we get
5) n sin φ = n' sin φ'
Using our assumption that the angle φ is small and sin θ ≅ θ, 5) can be written as
6) n φ = n' φ'
Substituting 3) into 6) gives
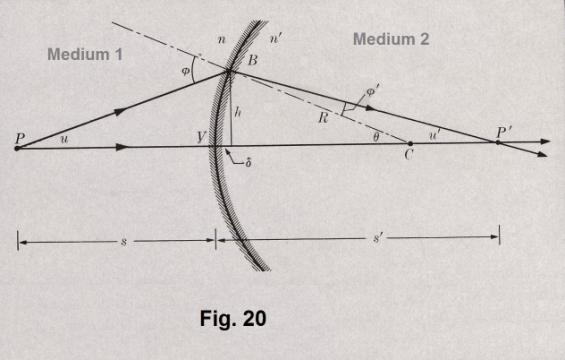
![]()
Substituting 7) into 4) gives
8)nu + n'u' = (n' - n)θ
The tangents of u, u', and θ are
![]()
Using our assumption that the angles u, u', and θ are small and that we can use the approximation tan θ ≅ θ and neglecting the small distance δ, 9) becomes
10) u = h/s, u' = h/s', θ = h/R
Substituting 10) into 8) gives
![]()
which is what we wished to show.
Prove. The magnification factor m is given by
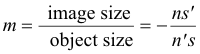
Proof. Referring to Fig. 21, we can obtain the image P'Q' of the object PQ by drawing two rays from point Q : 1. A ray from Q through the center of curvature C, and 2. A ray from Q incident at the vertex V. From triangles PQV and P'Q'V we have
![]()
From Snell’s law the refraction at V is given by
13) n sin φ = n' sin φ'
For small angles sin φ = tan φ and sin φ' = tan φ' so, substituting 12) into 13), we get
![]()
or
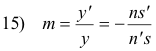
which is what we wanted to show.
Equations 1) and 2) can be applied to both convex and concave refracting surfaces and apply whether n' is greater or less than n.
Focal points of a spherical refracting surface. The concepts of focal point and focal length can also be applied to a spherical refracting surface. Such a surface has two focal points. The first is the object point when the image is at infinity and the second is the image point when the object is at infinity. These points lie on opposite sides of the surface and at different distances from it, so a single refracting surface has two focal lengths. The positions of these two focal points can be found from setting s or s' equal to infinity in equation 1).
The thin lens formula.
Theorem 3. For a thin lens
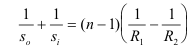
where so is the object distance, si is the image distance, n is index of refraction of the lens, R1 is the radius of curvature of the left lens surface, and R2 is the radius of curvature of the right surface.
Derivation. Most optical systems have more than one reflecting or refracting surface. In such systems the image formed by the first surface serves as the object for the second surface, the image for the second surface serves as the object for a third surface, etc. Such systems can be analyzed by using the equation
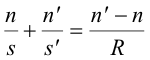
repeatedly, at each surface, to obtain the location of the final image of an object that is produced by the multi-surface system. Thus, in such problems, the image distance s' for one surface becomes the object distance s for the next surface. We can derive a relationship between the object distance s and the image distance s' for a thin lens using this technique. A lens has two refracting surfaces. Assume that the medium on both sides of the lens is air with an index of refraction of 1 and denote the index of refraction of the lens by n. Denote the radius of curvature of the left lens surface by R1 and the radius of curvature of the right surface by R2. Let s1 be the object distance for the first surface, s1' be the image distance for the first surface, s2 be the object distance for the second surface, s2' be the image distance for the second surface. Then for the refraction at the first surface we have
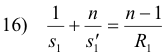
and for the refraction at the second surface
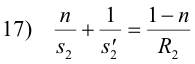
Now the object distance for the second surface will be the negative of the image distance for the first surface. Why the negative? Because of the convention that image distances to the right of the lens are considered positive while object distances to the right of the lens are considered negative. Thus if the image for the first surface is to the right of the lens, its distance s1' must become -s1' when considered as an object distance for the second surface. Thus
18) s2 = -s1'
Substituting 18) into 17) gives
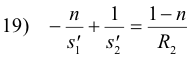
Adding 16) and 19) gives
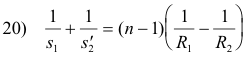
which can be rewritten as
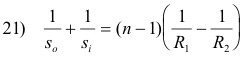
where so is the object distance and si is the image distance.
The lensmaker’s equation. One can find the focal length f of a thin lens by finding the image distance of an infinitely distant object. When so is infinity in 21), the value of si will be the focal length f. Substituting so = ∞ in 21) gives
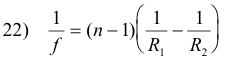
which is called the lensmaker’s equation.
From 21) and 22) we obtain
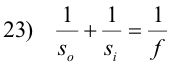
References
Dull, Metcalfe, Brooks. Modern Physics
Sears, Zemansky. University Physics
Semat, Katz. Physics
Freeman. Physics Made Simple
Bennett. Physics (COS)
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life