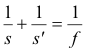
Website owner:  James Miller

Derivation of Lensmaker’s formula. Derive the formula

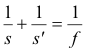
where

            s = distance of object from lens

            s' = distance of image from lens

            f = focal length of the lens

Derivation. We assume a thin, converging lens and that the light rays we are dealing with are close to the principal axis and make very small angles with the principal axis ( angles of less than 10^o), resulting in very small angles of incidence. Such rays are called paraxial rays. Thus we assume that the angles we are dealing with are small enough that we can approximate them by their sines and tangents (for very small angles, sin θ ≅ θ and tan θ ≅ θ). For definiteness the analysis will assume an object point that is located on the principal axis but the approximations made do not depend on this fact. The object and image relationships which will be derived will be equally valid for pairs of conjugate points lying on any line parallel to the principal axis. We will find that points lying on a plane perpendicular to the principal axis, called the object plane, will be imaged onto a second plane perpendicular to the principal axis, called the image plane. The lens is assumed to be constructed of a substance with a refractive index of n. The medium in which the lens is immersed is air with a refractive index of 1.

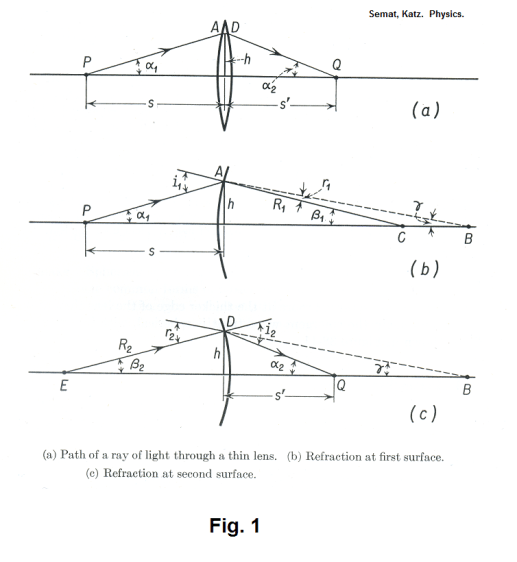
Referring now to Fig. 1(a), P is the object and Q is its image. An arbitrary ray passes from the object P to point A, is refracted at A, passes to point D, is refracted again at D, then passes to the image Q. Fig. 1(b) shows the refraction for the left surface of the lens. Point C is the center of curvature for the left surface of the lens and AC is normal to the lens surface. The refracted ray has the direction AB. The angle of incidence at point A is i₁ and the angle of refraction is r₁.

Using Snell’s law ( n₁ sin θ_i = n₂ sin θ_r ) at point A gives

1)        sin i₁ = n sin r₁

Using the small angle approximations sin i₁ = i₁ and sin r₁ = r₁, 1) becomes                       

2)        i₁ = n r₁

Now, using the theorem that states that the exterior angle of a triangle is equal to the sum of the two interior angles, we see from triangle ACP that

3)        i₁ = α₁ + β₁

and from triangle ABC that

4)        r₁ = β₁ - γ

Substituting 3) and 4) into 2) gives

5)        α₁ + β₁ = n(β₁ - γ)

Referring now to Fig. 1(c), the refracted ray AB never reaches point B on the principal axis but is refracted at the right surface of the lens at point D and then intersects the principal axis at point Q. Point E is the center of curvature of the right surface of the lens and ED is normal to the surface. Snell’s law gives, at point D,

6)        sin i₂ = n sin r₂

or, by our assumptions of small angles, 

7)        i₂ = n r₂

From triangle DEQ we see that

8)        i₂ = α₂ + β₂ 

and from triangle DEQ we see that

9)        r₂ = β₂ + γ

Substituting 8) and 9) into 7) we obtain

10)      α₂ + β₂ = n(β₂ + γ)

By eliminating γ from equations 5) and 10) we obtain

11)      α₁ + α₂ = (n - 1)(β₁ + β₂)

We now make a number of approximations consistent with the idea of a thin lens of small diameter. For example, we say that the distance from A to the principal axis is approximately equal to the distance from D to the principal axis and call it h. We say the object distance s is the distance from P to the lens, and the image distance s' is the distance from Q to the lens, neglecting the thickness of the lens. One can approximate a small angle by either its sine or its tangent and so we use the approximations α₁ = h/s, α₂ = h/s', β₁ = h/R₁, and β₂ = h/R₂. Substituting these relations into 11) gives

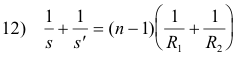
One can find the focal length f of a thin lens by finding the image distance of an infinitely distant object. When s is infinity in 12), the value of s' will be the focal length f. Substituting s = ∞ in 12) gives

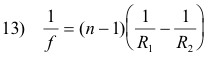
Equation 13 is called the lensmaker’s equation. Substituting 13) into 12) gives

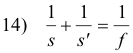
It can be shown that equations 12), 13), and 14) are applicable to all thin lenses through the use of the following sign conventions:

1. The radius of curvature R is positive for a convex surface and negative for a concave surface.

2. Light is assumed to come to the lens from the left.

3. The object distance s is positive when the object is to the left of the lens.

4. The image distance s' is positive when the image is to the right of the lens.

5. The focal length f is positive for a converging lens and negative for a diverging lens.

6. The positive and negative signs are to be used only when numerical values are substituted for the symbols.

The above equations were derived on the assumption that the lens was immersed in air. The equations are also correct when the lens are immersed in any medium, provided that n is interpreted as the relative index of the material of the lens with respect to the medium.

Reference.

  Semat, Katz. Physics.