Website owner:  James Miller

Prove. Theorem. The image formed by a plane mirror is erect, virtual, the same size as the object, and is located as far behind the mirror as the object is in front of it. Because the image is formed by a direct projection through the mirror, it is reversed (e.g. your right eye appears as the left eye in your image, etc.).

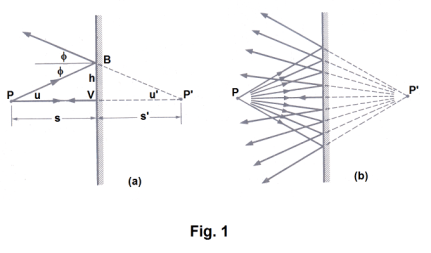
Proof. Consider Fig. 1(a) where P represents any arbitrarily chosen point of the object. We find the image P' of P by considering the reflected rays from various rays from P that might strike the mirror –– along with the extension of these reflected rays to the right of the mirror. The intersection of the extensions of these reflected rays to the right of the mirror give us the location of the image P'.

We first conveniently choose a ray from P perpendicular to the mirror, striking the mirror at V, and being reflected back on itself. The image P' must necessarily lie on the extension of this reflected ray to the right of the mirror. We next consider a ray PB, making an arbitrary angle u with PV. It reflects off the mirror at point B and the extension of the reflected ray to the right of the mirror must pass through the image point P'. Thus we have the triangle P'VB formed by these extensions. Now angle u' is equal to (Why? If two parallel lines are cut by a transversal, corresponding angles are equal.) and angle u is equal to (Why? If two parallel lines are cut by a transversal, the alternate interior angles are equal.), so u = u'. Since side VB is common to both triangles, triangles PVB and P'VB are congruent. Thus PV = VP'. PV is the distance s of P from the mirror and VP' is the distance s' of P' from the mirror. Thus s' = s.

Let us now note that the above result is true whatever the value of u. In other words, all rays diverging from P will appear to diverge from a common point P' after reflection from the mirror. See Fig. 1(b).

Thus we have established that the image is located the same distance behind the mirror as the object is in front of the mirror. That the image is erect is obvious since the image of each point P of the object lies on the extension of the normal from P to the mirror. That the image is virtual is obvious. Now let us show that the size of the image is the same as the size of the object. This also is obvious when we consider that the image P' of each point P of the object lies on that line through P that is perpendicular to the mirror and for each point P', s' = s. Thus the image must be the same size as the object.

Reference.

Sears, Zemansky. University Physics.