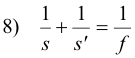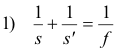
Website owner: James Miller
Prove. In a concave mirror the object distance s, image distance s', and focal length f are related by
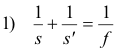
Proof. In Fig. 1, the center of curvature of the mirror is at C. The radius of curvature is R. An object point P on the principal axis is imaged into the point Q, also on the principal axis. The location of the image Q is determined by the intersection of two rays: 1) an arbitrarily chosen ray PA, reflected at point A and, 2) a ray directed from P through C along the principal axis.
The object distance s is the distance PV and the image distance s' is the distance QV. The radius CA represents the normal to the surface at point A and the angle of incidence and angle of reflection are equal and are both labeled θ. Other angles of interest are labeled α, β, and φ. AB is perpendicular to the principal axis at B and is of length h.
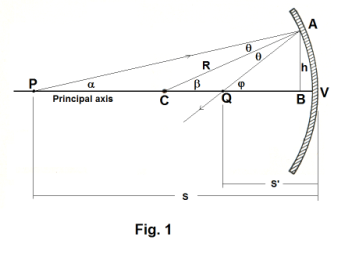
From triangle APC we see that
1) β = α + θ
(Why? The exterior angle of a triangle is equal to the sum of the interior angles.) and from triangle ACQ we see that
2) φ = β + θ
Subtracting 2) from 1) gives
3) α + φ = 2β
We make the assumption that we are dealing with rays that are very close to the principal axis and make very small angles with the principal axis ( angles of less than 10o), resulting in very small angles of incidence. Such rays are called paraxial rays. Thus we assume that the angles we are dealing with are small enough that we can approximate them by their tangents (for very small angles, tan θ ≅ θ). With this assumption we take the distance BV to be negligibly small, ignore it, and write:
4) α = tan α = h/s, β = tan β = h/R, φ = tan φ = h/s'
Substituting 4) into 3) we obtain
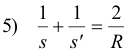
One can find the focal length f of a spherical mirror by finding the image distance of an infinitely distant object. When s is infinity in 5), the value of s' will be the focal length f. Substituting s = ∞ in 5) gives
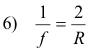
or
7) f = R/2
Substituting 6) into 5) gives