Measure theory. Measure of a point set. Open covering. Exterior and interior measure. Theorems. Borel sets.
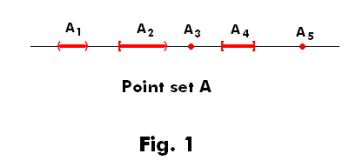
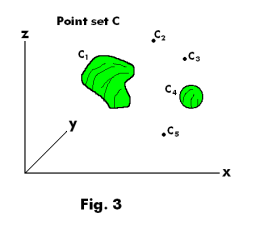
Point sets in one, two, three and n-dimensional space. Let us consider what we mean by a point set. An example of a point set in one-dimensional space is the point set A shown in Fig. 1 which consists of constituent point sets A1 thru A5. Point sets in one-dimensional space consist of sets of open, closed and half open /closed intervals of real numbers. An example of a point set in two-dimensional space is the point set B shown in Fig. 2 which consists of constituent point sets B1 thru B6. Fig. 3 shows an example of a point set in three-dimensional space and one can have similar point sets in n-dimensional space.
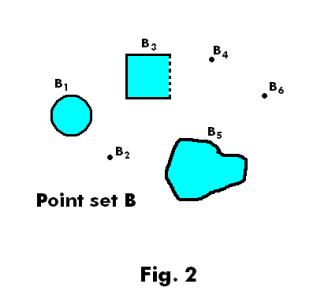
Concept of the measure of a set. The concept of the measure of a set is really very simple. In the case of a point set in one-dimensional space the measure of the set corresponds to the sum of the lengths of the component intervals defining the set. Thus the measure of point set A in Fig. 1 is the sum of the lengths of the intervals A1 thru A5. In the case of a point set in two-dimensional space the measure of the set corresponds to the sum of the areas of the component point sets in the set. Thus the measure of point set B in Fig. 2 is the sum of the areas of the component point sets B1 thru B6. In the case of a point set in three-dimensional space the measure of the set corresponds to the sum of the volumes of the component point sets in the set. Thus the measure of point set C in Fig. 3 is the sum of the volumes of the component point sets C1 thru C5. In the case of a point set in n-dimensional space the measure of the set corresponds to the sum of the n-dimensional volumes of the component point sets in the set.
Measure of a point set in one-dimensional space
Length of intervals. The unit of measurement is taken as the interval [0, 1]. The length of
all the intervals (a, b), [a, b], [a, b), and (a, b] is defined as b - a. The length of an infinite
interval such as (a,
) or (-
, b) is defined as
. In the case a = b, the interval [a, b]
degenerates to a point and has length zero.
We now define the measures of open and closed sets.
Measure of an open set. Any open set can be expressed as a countable union of mutually disjoint open intervals. The measure of an open set S is defined as the sum of the lengths of its constituent open intervals. Thus if
and the intervals (ai, bi) are pairwise disjoint, the measure of S is given as
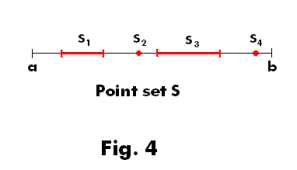
Measure of a closed set. Let S be a closed point set contained within an interval [a, b]. See Fig. 4. Then the measure of S is given by
mS = b - a - m
where
is the complement of S.
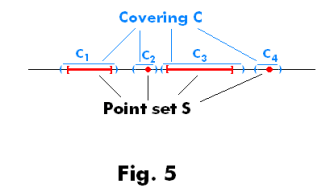
Def. Open Covering of a Set.
A set C of open intervals is said to be an open covering of a set S if every point of S belongs to some member of C (overlapping of the constituent open intervals of C is allowed). See Fig. 5.
We shall now give a definition of the measure of a general point set on the real line (a set which may, in general, be neither open nor closed).
Def. Exterior measure of a general point set on the real line. The exterior measure of a general point set S on the real line is defined as follows: Let C be an open covering for S. The exterior measure meS of S is the greatest lower bound of the sum of the measures of the constituent intervals of C for all possible coverings C. In other words, for each covering C, there is a number mc representing the sum of the measures of the constituent intervals of C. Corresponding to the set of all possible coverings C, there is a corresponding set of mc’s, and the exterior measure meS of S is the greatest lower bound (g.l.b. is smallest number in the set) of this set of mc’s. This measure is called the Lebesgue exterior (or outer) measure of S.
Def. Interior (or inner) measure of a general point set on the real line. Let S be a point set contained within an interval [a, b]. Then the interior (or inner) measure of S is defined as
miS = b - a - me
where
is the complement of S.
Measurable sets. A point set is said to be measurable if and only if its interior measure is equal to its exterior measure. If a point set S is measurable, then meS is its measure. Not all sets are measurable. If a set is not measurable it is said to have no measure. Although most point sets do have a measure and producing one that does not is difficult, point sets in the real line can be exhibited that do not.
Properties of a measurable set. The exterior or outer measure of a set S has the following properties which can be considered as axioms.
1) meS is defined for each set S
2) meS > 0
for all sets S1, S2, .....disjoint or not.
4) Exterior measure is translation invariant (if the point set is translated as a rigid body its measure does not change)
Theorem 1. The measure of the set of all rational numbers in the interval [0, 1] is zero.
Theorem 2. The measure of Cantor’s perfect set is zero.
From this theorem we see that a set may have the cardinality of the continuum and yet have a measure of zero.
Measure of a point set in n-dimensional Euclidean space
Intervals in n-dimensional space. The concept of an open or closed interval, (a, b) or [a, b], on the real line has been generalized for two, three and n-dimensional space.
Open interval. In 2-space an open interval is the rectangular area consisting of all points (x1, x2) satisfying
a1 < x1 < b1
a2 < x2 < b2
where a1, b1, a2, b2 are fixed constants. In 3-space it is the rectangular parallelepiped consisting of all points (x1, x2, x3) satisfying
a1 < x1 < b1
a2 < x2 < b2
a3 < x3 < b3
and in n-space it is the “generalized rectangular parallelepiped” consisting of all points (x1, x2, ....., xn) satisfying
a1 < x1 < b1
a2 < x2 < b2
..................
..................
an < xn < bn
for fixed constants ai, bi, i = 1, 2, ..... , n.
Closed interval. Closed intervals are defined in a similar fashion. A closed interval in n-space is the “generalized rectangular parallelepiped” consisting of all points (x1, x2, ....., xn) satisfying
a1
x1
b1
a2
x2
b2
..................
..................
an
xn
bn
for fixed constants ai, bi, i = 1, 2, ..... , n.
Measure of an interval in n-dimensional space. The measure of an interval in n-dimensional space defined by
a1
x1
b1
a2
x2
b2
..................
..................
an
xn
bn
is the product
(b1 - a1)(b2 - a2) .... (bn - an),
the same definition being used if the interval is open, closed, or partly open and partly closed.
Exterior measure of a point set in n-dimensional space. Let S be a set of points and C be a finite or countably infinite set of intervals (generalized intervals of n-space, open or closed) such that each point of S belongs to at least one of the intervals. The exterior measure of S is the greatest lower bound (g.l.b. is smallest number in the set) of the sum of the measures of the intervals of C, for all such sets C.
Interior measure of a point set in n-dimensional space. Let set S be contained in an
interval I and let
be the complement of S in I . Then the interior measure of S is the
difference between the measure of I and the exterior measure of
.
Measurable set. A bounded point set of n-dimensional space is (Lebesgue) measurable if its exterior and interior measures are equal, the common value being called the (Lebesgue) measure of the set.
****************************************************************************
Theorems
1. If a set E is measurable, then
is measurable and conversely.
2. If a set E has exterior measure zero, then E is measurable and m(E) = 0.
3. Any countable set has measure zero.
4. A countable sum of countable sets has measure zero.
5. A countable sum of measurable sets is measurable.
6. The intersection of a finite number of measurable sets is a measurable set.
7. The difference of two measurable sets is a measurable set.
8. If E1 and E2 are measurable sets, E1
E2, and E2 has finite measure, then E1 - E2 is
measurable and m(E2 - E1) = mE2 - mE1.
9. The intersection of a countable number of measurable sets is measurable.
10. If E1, E2, ..... are mutually disjoint measurable sets, then
m(E1
E2
) = mE1 + mE2 + ....
11. If E1, E2, E3, ..... are measurable sets such that E1
E2
E3
, then E = E1
E2
E3
is measurable.
12. If E1, E2, E3, ..... are measurable sets such that E1
E2
E3
, then E = E1
E2
E3
is measurable and
13. If E1, E2, E3, ..... are measurable sets such that E1
E2
E3
and at least one of the Ek
has finite measure, then E = E1
E2
E3
is measurable and
Almost everywhere properties. A property which is true except for a set of measure zero is said to hold almost everywhere.
Borel sets. The class of sets which can be obtained by taking countable unions or intersections of open or closed sets is called the class of Borel sets.
Theorem. Any Borel set is measurable.
Vitali’s covering theorem. Suppose that each point of a bounded, measurable set is covered by a class J of intervals having arbitrarily small size (called a Vitali covering). Then there exists a denumerable set of disjoint intervals I1, I2, I3, .... such
covers E except for a set of measure zero.
References
James and James. Mathematics Dictionary
Spiegel. Real Variables (Schaum)
Mathematics, Its Content, Methods and Meaning.
Natanson. Theory of Functions of a Real Variable