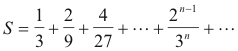
Prove. The measure of Cantor’s perfect set P is zero.

Proof. In constructing Cantor’s perfect set P from the interval [0, 1] we first removed an interval of length 1/3, then two intervals of length 1/9, then four intervals of length 1/27, etc. In general, after the n-th step we have removed 2^{n -1} intervals of length 1/3ⁿ. Thus the sum of the lengths of the intervals removed is equal to

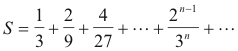
The terms of this series form a geometric progression with the first term 1/3 and the common ratio 2/3. Therefore the sum of the series is

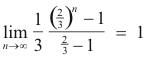
Thus the sum of the lengths of the intervals removed is 1. In other words, the measure of the open set Q complementary to P is 1. Thus the measure of P is

            mP = 1 - mQ = 1 - 1 = 0.