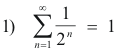
Prove. The measure of the set R of all rational numbers in the interval [0, 1] is zero.

The proof of the theorem utilizes the following theorem.

Theorem 1.

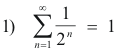
Proof. The derivation of 1) is as follows: The progression

is a geometric progression a, ar, ar², ar³ , .... where a = 1 and r = 1/2.. The sum of 2) over n terms

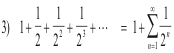
is given by the formula

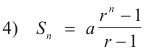
The sum of the progression 3) for n = is then given by

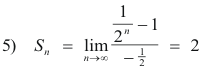
Thus, from 3),

Proof of main theorem: The measure of the set R of all rational numbers in the interval [0, 1] is zero.

We have already shown that the set R is countable. We now arrange the points of R in a sequence

            r₁, r₂, ... , r_n, ... .

Next, for a given ε > 0, we enclose the point r_n by an open interval C_n of length ε/2ⁿ. The sum C = Σ C_n is an open covering of set R. The open intervals C_n may intersect so the measure mC of C is given by

            mC = m(Σ C_n) < Σ mC_n = Σ (ε /2ⁿ) = ε

(where in the last equality we employ Theorem 1). Since ε can be chosen arbitrarily small, we have mR = 0, which is what we set out to prove.