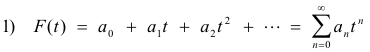
Website owner: James Miller
Methods of finding Laplace transforms and inverse transforms. Properties of inverse Laplace transforms. Convolution of two functions. Convolution theorem. Heaviside expansion formulas.
Methods of finding Laplace transforms
1. Direct method. Direct use of definition.
2. Use of tables.
3. Series method. If F(t) has a power series expansion given by
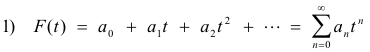
one can obtain its Laplace transform by taking the sum of the Laplace transforms of each term in the series. Thus the Laplace transform of 1) is given by
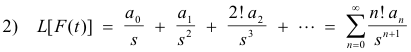
4. Method of differential equations. A method involving finding a differential equation satisfied by F(t) and then applying the various rules and theorems pertaining to Laplace transforms to obtain the desired transform f(s).
5. Differentiation with respect to a parameter. This method employs Leibnitz’s Rule for differentiating under an integral sign along with the various rules and theorems pertaining to Laplace transforms to arrive at the desired transform. See “Spiegel. Laplace Transforms (Schaum)” for examples.
6. Miscellaneous methods employing various devices and techniques.
Uniqueness of inverse Laplace transforms. The Laplace transform of a null function N(t) is zero. A consequence of this fact is that if L[F(t)] = f(s) then also L[F(t) + N(t)] = f(s). From this it follows that we can have two different functions with the same Laplace transform.
Example. The two different functions F1(t) = e-4t and
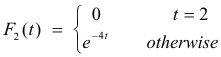
have the same Laplace transform i.e. 1/(s + 4)
Thus if we allow null functions, we can see that the inverse Laplace transform is not unique. It is unique, however, if we disallow null functions (which do not in general arise in cases of physical interest).
Lerch’s theorem. If a function F(t) defined on the positive real axis, t ≥0, is piecewise regular and of exponential order then the inverse Laplace transform is unique.
Inverse Laplace transforms
|
f(s) |
L-1[f(s)] = F(t) |
1. |
|
1 |
2. |
|
t |
3. |
|
|
4. |
|
|
5. |
|
|
6. |
|
cos at |
7. |
|
|
8. |
|
cosh at |
Properties of inverse Laplace transforms
1. Linearity property. Let c1 and c2 be any constants and F1(t) and F2(t) be functions with Laplace transforms f1(s) and f2(s) respectively. Then
3) L-1[c1 f1(s) + c2 f2(s)] = c1 L-1 [f1(s)] + c2 L-1 [f2(s)] = c1 F1(t) + c2 F2(t)
The inverse Laplace transform thus effects a linear transformation and is a linear operator.
Example.
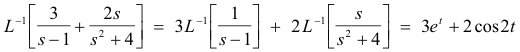
2. First translation (or shifting) property. If L-1[f(s)] = F(t), then
4) L-1[f(s - a)] = eat F(t)
Example 1. Since
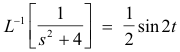
we obtain
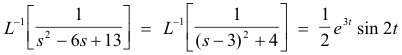
We can generalize on this example. Let a and b be arbitrary constants. Since
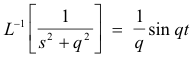
we can employ the method of completing the square to obtain the general result
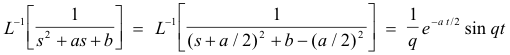
where
![]()
Remark. From item 3 in the above Inverse Laplace Transforms table we have
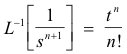
Applying 4) to this formula gives the following much used formula:
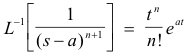
3. Second translation (or shifting) property. If L-1[f(s)] = F(t), then
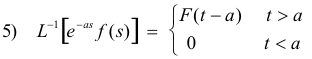
Example. Since
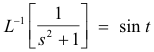
we obtain
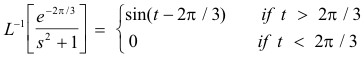
4. Change of scale property. If L-1[f(s)] = F(t), then
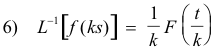
Example. Since
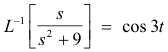
we obtain
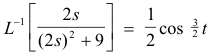
5. Inverse Laplace transform of derivatives. If L-1[f(s)] = F(t), then
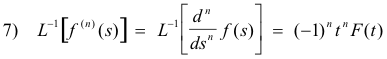
Example. Since
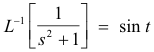
and
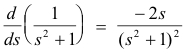
we obtain
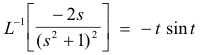
6. Inverse Laplace transform of integrals. If L-1[f(s)] = F(t), then
![]()
Example. Let
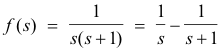
Then
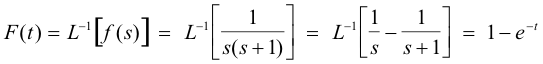
Now it can be shown that
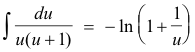
Consequently
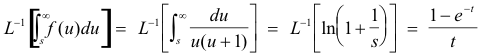
7. Multiplication by sn. If L-1 [f(s)] = F(t) and F(0) = 0, then
9) L-1 [sf(s)] = F'(t)
Thus multiplication by s has the effect of differentiating F(t). If F(0) ≠ 0, then
10) L-1 [sf(s) - F(0)] = F'(t).
Since, for any constant c, L [cδ(t)] = c it follows that L-1 [c] = cδ(t) where δ(t) is the Dirac delta function or impulse function. Thus 10) can be written
11) L-1 [sf(s)] = F'(t) + F(0)δ(t)
Generalizations of these results can be made for L-1 [sn f(s)], n = 2, 3, ......
Example. Since
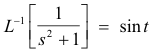
and sin 0 = 0, we obtain
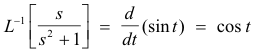
8. Division by s. If L-1 [f(s)] = F(t), then
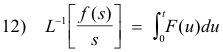
Example. Since
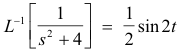
we obtain
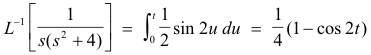
Def. Convolution of two functions. The function h defined by
![]()
is called the convolution of f and g and often denoted by f*g. It can be shown that f*g = g*f. Proof
9. Convolution theorem. Let L-1[f(s)] = F(t) and L-1[g(s)] = G(t). Then
![]()
Example. Since
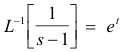
and
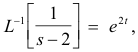
we obtain
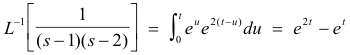
Methods of finding inverse Laplace transforms
1. Use of Tables
2. Method of partial fractions. Any rational function of the form p(s)/q(s) where p(s) and q(s) are polynomials in which p(s) is of lesser degree than q(s) can be written as a sum of fractions of the types
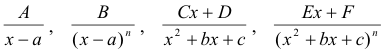
where n is a positive integer and all coefficients are real if all coefficients in the original polynomials were real. Fractions of these types are called partial fractions. The method consists of reducing a rational function p(s)/q(s) to a sum of partial fractions and then finding the inverse transform of that sum of partial fractions. For information on partial fractions and reducing a rational function p(s)/q(s) to a sum of partial fractions see Partial Fractions. A method closely related to this one uses the Heaviside expansion formula.
3. Heaviside expansion formulas.
Fundamental Theorem of Algebra. If g(x) is a polynomial with real coefficients, then g(x) can be written as the product of linear and quadratic factors with real coefficients:
g(x) = c(x - α1)(x - α2) ... (x2 + b1x + c1) (x2 + b2x + c2) ...
where bi2- 4ci < 0.
Theorem 1. Let y = L-1[p(s)/q(s)], where p(s) and q(s) are polynomials and the degree of q(s) is greater than the degree of p(s). Then the term in y corresponding to an unrepeated linear factor s - a of q(s) is given by
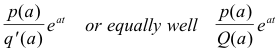
where Q(s) is the product of all the factors of q(s) except s - a.
Corollary. Let y = L-1[p(s)/q(s)]. Let q(s) be completely factorable into unrepeated linear factors
(s - a1), (s - a2), ........ , (s - an)
Then
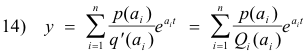
where Qi(s) is the product of all the factors of q(s) except the factor s - ai.
Theorem 2. Let y = L-1[p(s)/q(s)], where p(s) and q(s) are polynomials and the degree of q(s) is greater than the degree of p(s). Then the terms in y corresponding to a repeated linear factor (s - a)r in q(s) are
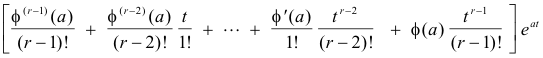
where f(s) is the quotient of p(s) and all factors of q(s) except (s - a)r.
Theorem 3. Let y = L-1[p(s)/q(s)], where p(s) and q(s) are polynomials and the degree of q(s) is greater than the degree of p(s). Then the terms in y corresponding to an unrepeated, irreducible quadratic factor (s + a)2 + b2 of q(s) are
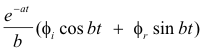
s
where fi and fr are, respectively, the real and imaginary parts of f(-a + ib) and f(s) is the quotient of p(s) and all the factors of q(s) except (s + a)2 + b2 .
There is a fourth theorem dealing with repeated, irreducible quadratic factors but because of its complexity and limited usefulness we will not present it.
Problem. Find
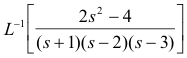
Solution. We have
p(s) = 2s2 - 4
q(s) = (s + 1)(s - 2)(s - 3) = s3 - 4s2 + s + 6
q'(s) = 3s2 - 8s + 1
a1 = -1, a2 = 2, a3 = 3
Then by 14) above the required inverse y = L-1[p(s)/q(s)] is given by
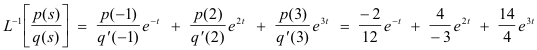
![]()
4. Series methods. If f(s) has a series expansion in inverse powers of s given by
![]()
then under suitable circumstances we can invert term by term to obtain
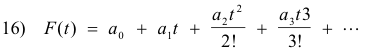
Problem. Find
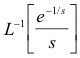
Solution. Expanding e-1/ s as an infinite series, we obtain
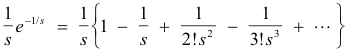
![]()
Inverting term by term, using Rule 3 in the above table of inverse Laplace transforms, we get
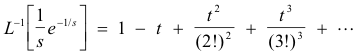
![]()
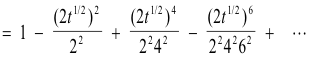
![]()
5. Method of differential equations. A method involving finding a differential equation satisfied by f(s) and then applying the various rules and theorems pertaining to Laplace transforms to arrive at the desired function F(t).
6. Differentiation with respect to a parameter. This method employs Leibnitz’s Rule for differentiating under an integral sign along with the various rules and theorems pertaining to Laplace transforms to arrive at the desired function F(t). See “Spiegel. Laplace Transforms (Schaum)” for examples.
7. The Complex Inversion formula. A method employing complex variable theory to evaluate the Complex Inversion formula.
8. Miscellaneous methods employing various devices and techniques.
References
Murray R. Spiegel. Laplace Transforms. (Schaum)
C. R. Wylie, Jr. Advanced Engineering Mathematics.
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life