Functional. Linear functional. Continuous linear functional. Conjugate space, dual space. Dual basis. Annihilator.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Def. Functional. A functional is a function T:A → F in which the domain A consists of a set of functions and the set F is a number field. In other words, it is a functional assignment that assigns to every function of some set a number.

Examples.

1. A function assigning to every function y = f(x), (a x b) the arc length of the curve it describes

2. A function assigning to every function y = f(x), (a x b) the value of its definite integral

3. In Hilbert space the inner product

where g(x) is a given, fixed function.

4. The problems of the calculus of variations in which we seek maxima and minima of sets of functions.

If we view a function f(x) as a point in an infinite dimensional space, then a functional is simply a function of the points of an infinite-dimensional space. From this point of view the problems of the calculus of variations are concerned with the search for maxima and minima of functions of points of an infinite-dimensional space.

Note. Different authors define the term functional differently and there is substantial variation.

Def. Linear functional. A functional T:V → F defined on a vector space V is linear if

T(av₁ + bv₂) = aTv₁ + bTv₂

for all vectors v₁ and v₂ and scalars a, b.

Def. Continuous linear functional. Norm of a functional. If a linear functional f :V → F has real or complex number values, then f is continuous for each x ε V if and only if there exists a number M such that

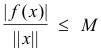
for each x (where ||x|| is the norm of x). The least such number M is called the norm of f and written || f ||.

Conjugate space. Let f be a continuous linear functional defined on a normed linear space N. The set of all such functionals is a complete normed linear space , or a Banach space, and is called the first conjugate space of N. The first conjugate space of this space is the second conjugate space of N, etc.

Syn. Adjoint space, dual space

If N is finite-dimensional, then N and its second conjugate space are identical (i.e. isometric).

For any normed linear space N, N is isometric with a subspace of its second conjugate space.

If N is a Hilbert space with a complete orthonormal sequence u₁, u₂, ..... , then the sequence of functions

f_n(x) = (x, u_n) [i.e. inner product x• u_n], n = 1, 2, .....

is a complete orthonormal sequence in the first conjugate space and the correspondence

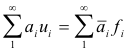
is an isometric correspondence between the two spaces.

James & James. Mathematics Dictionary

Dual basis. (1) For a finite-dimensional linear space V with a basis (x₁, x₂, ..... , x_n ), the dual basis is the set of linear functionals {f₁, f₂, ..... , f_n}defined by

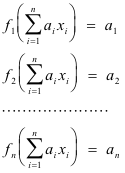
The dual basis is a basis for the first conjugate space V*. See Basis for Dual Space.

(2) If a Banach space (i.e. complete normed linear space ) has a basis (x₁, x₂, ..... ), then the sequence {f₁, f₂, ..... }defined by

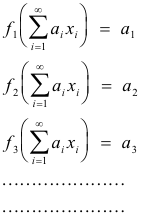
is a sequence of continuous linear functionals and it is a basis (a dual basis) for the first conjugate space if and only if it is shrinking in the sense that

for each continuous functional f, where || f ||_n is the norm of f as a continuous linear functional with domain the linear span of {x_n+1, x_n+2, ....}. This condition is satisfied by all bases in reflective spaces (Hilbert space is a reflective Banach space). If {x_α }is a complete orthonormal set for an inner product space T, then {f_α }is a complete orthonormal set for the first conjugate space of T, where

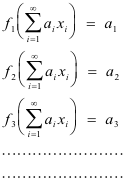
Analogously to (1), each of the orthonormal bases {x_α }and {f_α } is dual to the other.

James & James. Mathematics Dictionary

Annihilator. An annihilator of a set S is the class of all functions of a certain type which annihilate S in the sense of being zero at each point of S. For example, if S is a subset of a normed linear space N, then the annihilator of S is the linear subset S' of the first conjugate space N* consisting of all continuous linear functionals which are zero at each point of S.

Let W be a subset (not necessarily a subspace) of a vector space V and V* be the first conjugate space of V. A linear functional f V* is called an annihilator of W if f(w) = 0 for every w W. The set of all such mappings, denoted by W⁰ and called the annihilator of W, is a subspace of V*.

Example 1. Pass a line through the origin of an x-y-z Cartesian coordinate system and label it L. Let W be the set of all vectors in line L. Pass a plane through the origin of the coordinate system perpendicular to line L and label it K. Let S represent the set of all vectors in plane K. Then S is an annihilator of W. Why? If s is any vector in S and w is any vector in W then the dot product s∙w = 0. The vector s can be viewed as a linear operator (linear functional) mapping the vectors of W into the field of reals and it maps all the elements of W into zero. By the same logic W is an annihilator of S. So the annihilator W⁰ of W is the set S and the annihilator S⁰ of the set S is the set W.

Example 2. The annihilator of a linear subset S of Hilbert space is the orthogonal complement of S.

References

James & James. Mathematics Dictionary