Measurable functions. Theorems. Baire classes. Egorov�s theorem.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Measurable functions. Theorems. Baire classes. Egorov’s theorem.

Def. Measurable function. Let f(x) be a real-valued function defined on a measurable set E. The function f(x) is said to be (Lebesgue) measurable if for any real number α the set of all x for which f(x) > α is measurable.

Let us consider this concept more carefully. Let us denote by

E[f(x) > α]

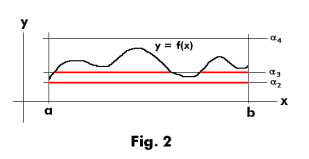
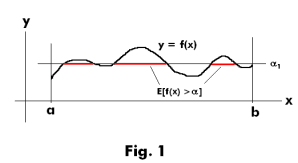
that set of values x ε E for which f(x) > α . Consider the function y = f(x) shown in Fig. 1, defined on the open interval (a, b). Here the set E corresponds to the real numbers in the interval (a, b). A value of α = α₁ is shown and the red line segments indicate the subset of E for which f(x) > α. In Fig. 2 some other values for α are shown along with the subsets of E for which f(x) > α. The function f(x) is called measurable only if all these subsets of E for the different values of α are measurable.

Theorems

1. The function f(x) is measurable on a measurable set E if and only if for each real number α one of the following sets is measurable

(a) E[f(x) < α]

(b) E[f(x) α]

(d) E[f(x) α]

Consequently, the above conditions represent four equivalent definitions for a measurable function.

2. If function f(x) is measurable on a set E, then E[f(x) = α] is measurable for each α. The converse is not true.

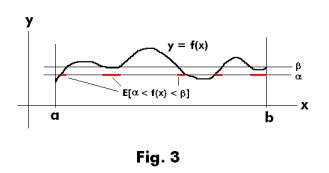
3. The function f(x) is measurable on a set E if and only if for each pair of distinct real numbers α and β, E[α < f(x) < β] is measurable. The result is also true if either one or both of the inequality symbols is replaced by ≤.

In Fig. 3 we see, in red, a point set corresponding to this criterion.

4. A function f(x) is measurable on a set E, if E[f(x) > α] is measurable for each rational number α.

5. If function f(x) is measurable on a set E₁ and if E₂ E₁, then f(x) is measurable on E₂.

6. If f(x) is measurable on a countable class of disjoint set E₁, E₂, E₃, ...... , then it is measurable on their union E₁ ∪ E₂∪ E₃∪ ...

7. If f₁(x) and f₂(x) are measurable on a set E, then E[f₁(x) > f₂(x)] is measurable.

8. A constant function is measurable.

9. If function f(x) is measurable on a set E, then for any constant c, f(x) + c and c f(x) are also measurable on E.

10. If a function f(x) is measurable on a set E, then [f(x)]² is measurable on E.

11. If f₁(x) and f₂(x) are measurable on a set E, then f₁(x) + f₂(x), f₁(x) - f₂(x), f₁(x)f₂(x), and f₁(x)/f₂(x) where f₂(x) ≠ 0 are measurable on E i.e. the sum, difference, product and quotient of measurable functions is also measurable (the quotient only if the denominator is non-zero).

12. If f₁(x) and f₂(x) are measurable on a set E, then the maximum of f₁(x) and f₂(x) i.e. max {f₁(x), f₂(x)} is measurable. Similarly, the minimum of f₁(x) and f₂(x) i.e. min {f₁(x), f₂(x), is measurable.

13. If a function f(x) is measurable on a set E, then |f(x)| is measurable on E.

14. If a function f(x) is continuous on E, it is measurable on E.

15. If f₁(u) is continuous and u = f₂(x) is measurable, then f₁(f₂(x) ) is measurable. In other words, a continuous function of a measurable function is measurable. However, a measurable function of a measurable function need not be measurable.

16. Let {f_n(x)}be a sequence of measurable functions on a set E. Then F(x) = l.u.b. f_n(x), called the upper boundary function, and G(x) = g.l.b. f_n(x), called the lower boundary function, are also measurable on E.

17. If {f_n(x)} be a monotonic sequence of measurable functions on a set E such that

then f(x) is measurable on E.

Note. The sequence {f_n(x)}is said to be monotonic increasing if f₁(x) ≤ f₂(x) ≤... , monotonic decreasing if f₁(x) ≥ f₂(x) ≥... , and monotonic if the sequence is monotonic increasing or monotonic decreasing.

18. Let {f_n(x)}be a sequence of measurable functions on a set E. Then lim sup f_n(x) and lim inf f_n(x) are measurable on E.

19. If a sequence {f_n(x)} of measurable functions defined on a set E converges almost everywhere to a function f(x), then this function is also measurable.

20. If a function f(x) is measurable on a set E and f₁(x) = f₂(x) almost everywhere on E, then f₂(x) is measurable on E.

An important question. If a sequence {f_n(x)} of measurable functions defined on a set E converges at every point of E, except possibly at the points of a set of measure zero, then the sequence is said to converge almost everywhere. An important and central question in the theory of real variables is the following:

Q. What functions can be obtained from continuous functions by repeated application of the operation of forming the limit of an almost everywhere convergent sequence of functions and of algebraic operations?

A. Theorems 11, 14 and 19 give the answer. Continuous functions on a measurable set E are measurable and if a sequence {f_n(x)} of continuous functions on E converges almost everywhere to a function f(x), then this function is also measurable. The sum, difference, product and quotient of measurable functions is also measurable.

We note that the limits of convergent sequences of continuous functions may be discontinuous. For an example, see Example 1 in Series . We thus see that the limits of convergent sequences of continuous functions, which may be discontinuous, are measurable and that the limits of these discontinuous functions are measurable, etc. We thus obtain a hierarchy of measurable functions.

Baire classes. The above considerations led Baire to give a classification of functions. A function is said to belong to the Baire class of order zero (or briefly Baire class 0) if it is continuous. A non-continuous function which is the limit of a sequence of continuous functions (i.e. functions belonging to Baire class 0) belongs to Baire class 1. In general, a function is said to belong to Baire class p if it is the limit of a sequence of functions of Baire class p - 1 but does not itself belong to any of the Baire classes 0, 1, ..... , p -1. Thus every function that belongs to some Baire class is measurable.

Egorov’s theorem. Let {f_n(x)} be a sequence of measurable functions which converges to a finite limit f(x) almost everywhere on a set E of finite measure. Then given any number δ > 0, there exists a set F of measure greater than mE - δ on which the sequence converges to f(x) uniformly.

References

James and James. Mathematics Dictionary

Spiegel. Real Variables (Schaum)

Mathematics, Its Content, Methods and Meaning.

Natanson. Theory of Functions of a Real Variable