Series of variable terms, uniform convergence, power series, interval of convergence

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

SERIES OF VARIABLE TERMS, UNIFORM CONVERGENCE, POWER SERIES, INTERVAL OF CONVERGENCE

Series of variable terms. We often have to deal with series whose terms are functions of a variable x, series such as the following

The first of these is called a power series in x, the second is a power series in (x - 2) and the third is called a trigonometric series.

In general, series in some variable x are convergent for some values of the variable and divergent for others. A power series, for example, is convergent for all values of x in a certain interval, called the interval of convergence, and divergent for all values of x outside this interval.

Concept of uniform convergence. When working with series whose terms are functions of some variable x the necessity arises for differentiating them term by term, integrating them, deciding whether their sum is continuous, etc. For the familiar case of the regular algebraic or transcendental expressions that one is accustomed to working with in mathematics (e.g. expressions such as 2x² + 1, 2 x² + 5 sin3x + 2, 3 x³ + log x + 1, etc.), a situation in which we are dealing with the sum of a finite number of terms, there are simple general rules in regard to differentiating them, integrating them, etc.. We know, for example, that in the case of such expressions:

1. The derivative of the sum of differentiable functions is equal to the sum of their derivatives.

2. The integral of a sum of continuous functions is the sum of their integrals.

3. A sum of continuous functions is itself a continuous function..

Now the three rules just stated above hold when we are speaking of the sum of a finite number of terms. However, for infinite series these three simple rules are, in general, no longer true. There are many examples of convergent series of functions for which the rules of term-wise integration and differentiation don’t hold. In the same way a series of continuous functions may turn out to have a discontinuous sum. On the other hand there are also many infinite series that do behave like finite sums with respect to these rules.

Deep investigations into this question in the early 1800's led to the important concept of the uniform convergence of a series.

Let us consider the series

4) S(x) = u₁(x) + u₂(x) + u₃(x) + ....

whose terms u_i(x) are functions defined on the interval [a, b]. Let the partial sums of the first n terms of the series be

5) S_n(x) = u₁(x) + u₂(x) + ... +u_n(x) .

These partial sums are also functions of x defined on [a, b]. These partial sums form an infinite sequence of functions which may or may not converge to some limiting function.

Let us now direct our attention to the question of the conditions under which a series of functions

{f_n(x)}, n = 1, 2, 3, ...

will converge to a limiting function.

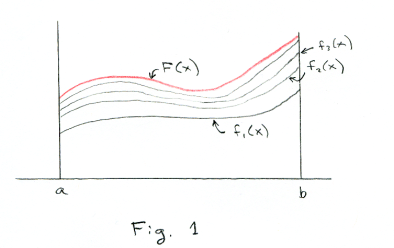
Convergence of an infinite sequence of functions. Let {f_n(x)}, n = 1, 2, 3, ... be an infinite sequence of functions defined on interval [a, b]. See Fig. 1. The sequence is said to converge to F(x), or to have the limit F(x) on [a, b], if for any chosen ε > 0 and each x in [a, b] we can find an N > 0 such that |F(x) - f_n(x)| < ε for all n > N. In such a case we write The number N may depend on x as well as ε. If it depends only on ε and not on x, the sequence is said to converge to F(x) uniformly on [a, b] or to be uniformly convergent on [a, b]. If a sequence is convergent but not uniformly convergent it is said to be nonuniformly convergent.

We now make an important observation. Let us suppose that the infinite sequence of functions

{f_n(x)}, n = 1, 2, 3, ...

converges (not necessarily uniformly) to the function F(x). We observe that it is possible for all the functions f_n(x) in the sequence to be continuous and yet for the limiting function F(x) to be discontinuous. We give an example:

Example 1. Consider the infinite sequence of functions {f_n(x) = xⁿ,}, n = 1, 2, 3, ... defined on interval [0, 1]. See Fig. 2. Define

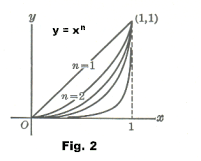
The sequence is convergent if . Note that every function in the sequence is continuous over the interval [0, 1]. Now note that the limiting function F(x) is given by

F(x) = 0 if 0 x < 1

F(1) = 1

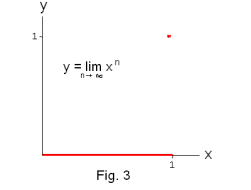
See Fig. 3. We see that the limiting function F(x) has a discontinuity at x = 1. Thus all the functions of the sequence are continuous but the limiting function is discontinuous.

We thus see how a function f_n(x) (whose shape changes with increasing n) and the limiting function F(x) that f_n(x) approaches as a limit can be fundamentally different functions, functions with different basic characteristics. This fact causes difficulties and creates a need for careful analysis.

Note that in this example just cited, for every individual value of x in the interval [0, 1],

One might be tempted to think that if condition 7) held then and F(x) would necessarily be identical functions but, as this example shows, this is not necessarily the case.

Let us now go again to the question of the conditions under which a sequence of functions

{f_n(x)}, n = 1, 2, 3, ...

will converge uniformly to a limiting function F(x). We assume that the sequence converges to F(x) but ask under what conditions it will converge uniformly to F(x).

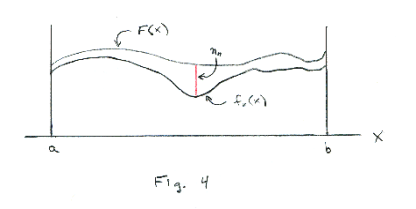
We introduce a magnitude η_n, which is equal to the least upper bound of the values |F(x) - f_n(x)|, as x varies on the interval [a, b]. This magnitude is written as

See Fig. 4.

From our assumed convergence of our series, we have for every individual value of x in the interval [a,b]

The magnitude η_n may approach zero or it may not as n increases. An example of a case in which it does not can be found in Example 1 above. In Example 1 the quantity | F(x) - f_n(x) | is arbitrarily close to unity for x close to x = 1 and thus

for all n = 1, 2, ... .

Theorem 1. A convergent sequence of functions {f_n(x)}, n = 1, 2, 3, ... is uniformly convergent if and only if η_n approaches zero as n → ∞.

Thus in Example 1 above the sequence of functions is convergent but not uniformly convergent.

Mathematics, Its Content, Methods and Meaning. Vol I, p. 172

Spiegel. Advanced Calculus. p. 227

Taylor. Advanced Calculus. p. 587

Theorems on infinite sequences of functions.

Theorem 2. Let the infinite sequence of functions {f_n(x)}, n = 1, 2, 3, ... be defined on the interval [a, b], and let them converge uniformly on this interval to the limit function F(x). Then, if each of the functions f_n(x) is continuous at a point x₀, the limit function F(x) is also continuous at x₀. In particular, if each f_n(x) is continuous on the whole interval, so is F(x).

Theorem 3. Let the infinite sequence of functions {f_n(x)}, n = 1, 2, 3, ... be defined on the interval [a, b], and let them converge uniformly on this interval to the limit function F(x). Then

Theorem 4. Let the infinite sequence of functions {f_n(x)}, n = 1, 2, 3, ... be defined and have continuous derivatives on the interval [a, b] and let them converge on this interval to the limit function F(x). Let the infinite sequence of functions {f_n'(x)}, n = 1, 2, 3, ... be uniformly convergent on [a, b]. Then F(x) is differentiable and

Uniform convergence of a series. The infinite series

Σ u_n(x) = u₁(x) + u₂(x) + u₃(x) + ...

is said to be convergent on an interval [a, b] if the sequence of partial sums {S_n(x)}, n = 1, 2, 3, ... , where S_n(x) = u₁(x) + u₂(x) + ... + u_n(x), is convergent on [a, b]. In such as case we write and call S(x) the sum of the series. Here the partial sums S_n(x) constitute an infinite sequence of functions, such as we have just mentioned above, in which the limiting case is S(x).

It now follows that Σu_n(x) converges to S(x) on [a, b] if for any chosen ε > 0 and each x in [a, b] we can find an N > 0 such that |S_n(x) - S(x)| < ε for all n < N. If N depends only on ε and not on x, the series is called uniformly convergent on [a, b].

Since S(x) - S_n(x) = R_n(x), the remainder after n terms, we can equivalently say that Σu_n(x) is uniformly convergent on [a, b] if for any chosen ε > 0 we can find N depending on ε but not on x such that |R_n(x)| < ε for all x in [a, b].

Spiegel. Advanced Calculus. p. 227

Example 2. Consider the series

which we take to be defined only for nonnegative values of x, namely on the half line [0, ). A little manipulation will show that 8) can be written as

from which we see that its partial sums are equal to

and

Thus the series is convergent for all nonnegative x and has the sum S(x) = 0. Furthermore,

so that the series is uniformly convergent to zero on the half axis [0, ).

Example 3. The series

x + x(x-1) + x²(x-1) + ...

may be written in the form

x + (x² -x) + (x³ - x²) + ...

from which

S_n(x) = xⁿ,

and therefore

Thus the sum of the series is discontinuous on the interval [0, 1] with a discontinuity at the point x = 1. The quantity | S(x) - S_n(x) | is arbitrarily close to unity for x close to x = 1 and thus

for all n = 1, 2, ... . Thus the series is nonuniformly convergent on the interval [0, 1].

Mathematics, Its Content, Methods and Meaning. Vol I, p. 172, 173

Tests for uniform convergence of a series.

1. Weirstrass M test. If a sequence of positive constants M₁, M₂, M₃, ... can be found such that in some interval

(a) |u_n(x)| M_n n = 1, 2, 3, ...

(b) ΣM_n converges

then Σu_n(x) is uniformly and absolutely convergent on the interval.

Example.

2. Dirichlet’s test. Suppose that

(a) the sequence {a_n} is a monotonic decreasing sequence of positive constants having limit zero,

(b) there exists a constant P such that for

| u₁(x) + u₂(x) + ... + u_n(x) | < P for all n > N.

Then the series

is uniformly convergent on the interval .

Theorems on uniformly convergent series.

As a corollary of Theorem 2 we have:

Theorem 5. If the terms of an infinite series are continuous on an interval , and if the series is uniformly convergent on the interval, the function defined as the sum of the series is continuous on the interval.

Taylor. Advanced Calculus. p. 598

Def. Differentiation of a an infinite series. The term-by-term differentiation of the series. Let the series

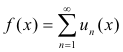
be convergent over some interval [a, b] and let each term u_i(x) have a continuous derivative on the interval. Let the series of derivatives

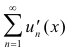
be uniformly convergent over the interval. Then

Any power series satisfies this condition in any interval within its interval of convergence.

Example. The series

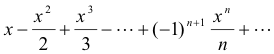
converges for -1 < x < 1 and represents log(1 + x) in this interval; the derived series

1 - x + x² - ... x^n-1 ...

converges uniformly for -a < x < a if a < 1, and represents

in any such interval.

Def. Integration of an infinite series. The term-by-term integration (definite integration) of an infinite series. If a series

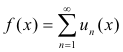
converges uniformly on the closed interval [a, b] and if the terms u_i(x) are continuous on the interval, then

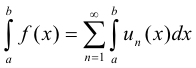
i.e. it may be integrated term by term and the result will converge and equal the integral of the function represented by the original series, provided the limits of integration are finite and lie within the interval of uniform convergence

Any power series satisfies this condition in any interval within its interval of convergence and may be integrated term by term provided the limits of integration lie within the interval of convergence. The series

1 - x + x² - ... (-1)ⁿ⁺¹x^{n -1} ...

converges when |x| < 1. Hence term by term integration is permissible between the limits 0 and 1/2, for instance, or between x₁ and x₂, provided |x₁| < 1 and |x₂| < 1.

James and James. Mathematics Dictionary.

Power series. A series of the form

10) a₀ + a₁x + a₂x² + ... + a_nxⁿ + ... ,

involving positive integral powers of a variable x and constant coefficients a_i is called a power series in x. It is an immediate generalization of the polynomial a₀ + a₁x + a₂x² + ... + a_nxⁿ . A series of the form

11) a₀ + a₁(x - a) + a₂(x - a)² + ... + a_n(x - a)ⁿ + ... ,

is called a power series in x - a.

If in the power series 10) a particular value is assigned to x, the series is reduced to a series of constants which may or may not converge. It is apparent that it converges for the value x = 0 but it might not converge for any other value of x. Or again it might converge for all values of x. If the power series 10) converges for x = b, then it will converge for all values of x such that |x| < b. If it diverges for x = b, then it will diverge for all values of x such that |x| > b.

Let us apply the ratio test to power series 10). The ratio test says that the series will converge if L < 1 where

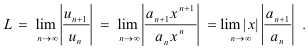
Thus the series will converge if

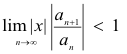
or, equivalently, if

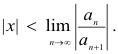
Theorem 6. The power series

a₀ + a₁x + a₂x² + ... + a_nxⁿ + ...

converges when

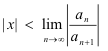
and diverges when

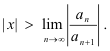
The series may or may not converge when

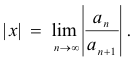
● The totality of points at which the series converges makes up the interval of convergence, the end points of the interval being

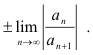
Example. Find the interval of convergence of the series

Solution.

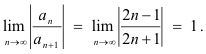
Therefore, by the theorem, the series converges for |x| < 1 or in the interval -1 < x <1. At end point x = -1 the series is an alternating series and is convergent. At end point x = 1 the series is again a convergent alternating series. Therefore the interval of convergence is -1 x 1.

Oakley. The Calculus. p. 185-186

By the same analysis as above we have a corresponding theorem for the case of a power series in x - a:

Theorem 7. The power series

a₀ + a₁(x - a) + a₂(x - a)² + ... + a_n(x - a)ⁿ + ...

converges when

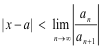
and diverges when

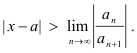
The series may or may not converge when

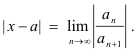
Def. Permanently convergent series. A permanently convergent series is one which is convergent for all values of the variable, or variables, involved in its terms; e.g., the exponential series,

1 + x + x²/2! + x³/3! + ... ,

is equal to e^x for all values of x; hence the series is permanently convergent.

James and James. Mathematics Dictionary.

Def. Interval of convergence. A power series,

c₀ + c₁(x - a) + c₂(x - a)² + ... + c_n(x - a)ⁿ + ... ,

either converges for all values of x, or there is a number R such that the series converges if |x - a| < R and diverges if |x - a| > R. The interval (a - R, a + R) is the interval of convergence (R may be zero). The series converges absolutely if |x - a| < R and converges uniformly in any interval (A, B) with a - R < A B < a + R.

James and James. Mathematics Dictionary.

Def. Circle of convergence. For a power series,

c₀ + c₁(z - a) + c₂(z - a)² + ... + c_n(z - a)ⁿ + ... ,

there is a number R such that the series converges (absolutely) if |z - a| < R and diverges if |z - a| > R. The circle of radius R with center at a in the complex plane is the circle of convergence (its equation is |z - a| < R ); R is the radius of convergence (R may be zero or infinite). The series converges uniformly in any circle with center at a and radius less than R. The series may either converge or diverge on the circumference of the circle.

Example. The power series

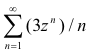
converges absolutely within the circle whose radius is 1/3 and whose center is the origin, and diverges outside this circle. It converges for z = -1/3, but diverges for z = +1/3.

James and James. Mathematics Dictionary.

References.

Mathematics, Its Content, Methods and Meaning. Vol I, p. 171 - 178

James and James. Mathematics Dictionary.

Middlemiss. Differential and Integral Calculus. 414 - 415

Oakley. The Calculus. p. 185-186

Taylor. Advanced Calculus. Chap. 18.

Spiegel. Advanced Calculus.