The elementary functions. Definitions of trigonometric, exponential, logarithmic, and hyperbolic functions.

SolitaryRoad.com

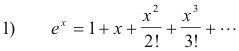
Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

The elementary functions

We shall now consider the basic definitions of those elementary functions most commonly met in mathematics:

∙ the exponential functions a^x, e^x

∙ the logarithmic functions log x, ln x

∙ the trigonometric functions sin x, cos x, tan x, cot x, sec x, csc x

∙ the hyperbolic functions sinh x, cosh x, tanh x, coth x, sech x, csch x

∙ the inverse trigonometric and hyperbolic functions

We wish to briefly sketch the process in which they have been defined, redefined, then redefined again with each redefinition representing an extending and broadening of a previous definition. We start first with the case where the argument x is a real number. Then we give their definitions when the argument x is a complex number.

Case 1. Argument a real number.

The exponential functions a^x, e^x. First we define a meaning to a^x when a and x are real numbers. The process is a multi-step one. We first define a^x for the case where x is a positive integer, then define it for the case when x is a rational number ( i.e. a quotient of two integers), then finally define it for the case when x is a real number. For details see the following:

The exponential and logarithmic functions

Since e^x is a special case of a^x (where a is equal to the special number e), no separate definition is required for e^x.

Computation of values of a^x, e^x. The value of e^x can be obtained from its Maclaurin series expansion. The expansion is

Derivation

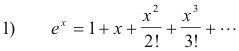
The value of a^x can be computed from the relation a^x = e^{x ln a}.

Proof

Thus we substitute “x ln a” for x in 1) above to compute the value of a^x.

The logarithmic functions log x, ln x. The logarithmic function log_ax (a>1 and a and x are real) is defined as the inverse of the function a^x . More specifically, if

x = a^y

then

y = log_a x .

The function ln x = log_ex is a special case of log_a x, needing no special definition.

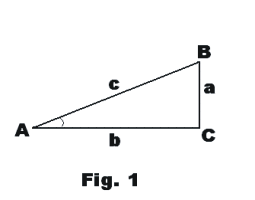
The trigonometric functions sin x, cos x, tan x, cot x, sec x, csc x. The basic definitions of the various trigonometric functions are given in terms of the acute angles of a right triangle. See Fig. 1. Shown is a right triangle in which C is the right angle, the side opposite being the hypotenuse c. In terms of this right triangle of Fig. 1 the definitions are as follows:

sin A = a/c cos A = b/c

tan A = a/b cot A = b/a

sec A = c/b csc A = c/a

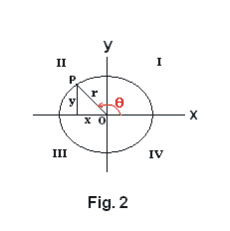
The definition of the trigonometric functions is then broadened in such a way as to define meanings for the functions for all angles, not just the angles between 0^o and 90^o. The broadened definition utilizes the Cartesian coordinate system shown in Fig. 2. Let P(x, y) be a point on a circle of radius r and let θ be the angle measured counterclockwise from the positive x axis to line OP. Then the trigonometric functions are defined as follows:

The coordinate system is divided into four quadrants — quadrants I, II, III, and IV --- as shown in the figure. The values of x are positive to the right of the origin and negative to the left of it, as usual, and the values of y are positive above the origin and negative below it. The signs of the functions change from quadrant to quadrant, depending on the signs of the x and y coordinates of point P. The angle θ can be either positive or negative, with the counterclockwise direction considered as positive, and is generally measured in either degrees or radians. Angles can be of any size — point P can make multiple trips around the origin.

It will be noted that for angles in the first quadrant the functions have the same values as in the previous definition.

Computation of values of the trigonometric functions. The values of sin x and cos x can be obtained from their Maclaurin series expansions. The expansion for sin x is

Derivation

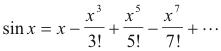
The series can be shown to converge for all values of x. It can be used to compute the value of sin x for any value of x.

The Maclaurin series expansion for cos x is

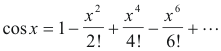
Once we have computed either sin x or cos x we can compute the other through the identity sin²x + cos²x = 1. The other trigonometric functions can then be computed through relations such as tan x = sin x / cos x, cot x = 1 /tan x, sec x = 1/cos x, csc x = 1/sin x.

The hyperbolic functions sinh x, cosh x, tanh x, coth x, sech x, csch x . Given an equilateral hyperbola x² - y² = a² shown in Fig. 4, hyperbolic functions are defined by ratios connected with that hyperbola that are similar to those defining the trigonometric functions. Let u = 2A/a² where A is the shaded area OPQ shown in Fig. 4 and a = OQ. Then

hyperbolic sine u = sinh u = y/a

hyperbolic cosine u = cosh u = x/a

hyperbolic tangent u = tanh u = y/x

hyperbolic cotangent u = coth u = x/y

hyperbolic secant u = sech u = a/x

hyperbolic cosecant u = csch u = a/y

The quantity u = 2A/a² plays the role played by the angle θ in trigonometric functions.

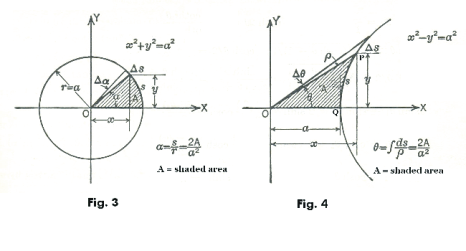
Hyperbolic angles. Hyperbolic angles are defined in a manner similar to circular angles but with reference to an equilateral hyperbola. The comparative relations are shown in figures 3 and 4. A circular angle is an angle measured in radians by the ratio s/a or, equivalently, the ratio 2A/r², where A is the area of the sector included by the angle α and the arc s (Fig. 3). For the hyperbola the radius ρ is not constant. Here the value of the differential hyperbolic angle dθ is defined by the ratio ds/ρ. Then θ = S ds/ρ = 2A/a², where A represents the shaded area OPQ in Fig. 4. If both s and ρ are measured in the same units the angle is expressed in hyperbolic radians.

From Eshback. Handbook of Engineering Fundamentals. p. 2-76

Computation of values of the hyperbolic functions. The Maclaurin series expansions of sinh x and cosh x are

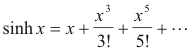
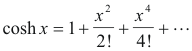
The other functions can then be computed from

tanh x = sinh x/cosh x

coth x = 1/tanh x

sech x = 1/cosh x

csch x = 1/sinh x

The functions sinh x and cosh x are also given by

sinh x = (e^x - e^-x)/2

cosh x = (e^x + e^-x)/2

Proof

Additional formulas.

sinh (-x) = - sinh x

cosh (-x) = cosh x

cosh² x - sin²x + 1

sech² x + tanh² x = 1

coth² x + csch² x = 1

Inverse trigonometric functions. The inverse trigonometric functions sin^-1 x, cos^-1 x, tan^-1 x, etc are implicitly defined through the definitions of sin x, cos x, tan x, etc. For example, if u = sin θ, then θ = sin^-1 u, by definition. The inverse functions are multiple-valued and it is necessary to select a particular interval for the principal values.

Inverse hyperbolic functions. The inverse trigonometric functions sinh^-1 x, cosh^-1 x, tanh^-1 x, etc are implicitly defined through the definitions of sinh x, cosh x, tanh x, etc. For example, if u = sinh θ, then θ = sinh^-1 u, by definition. The inverse functions are multiple-valued and it is necessary to select a particular interval for the principal values.

***********************************

Case 2. Argument a complex number. We will now treat the manner in which meanings have been assigned to the various elementary functions when the arguments are complex numbers.

The exponential functions a^z, e^z. We define meanings to a^z and e^z when z is a complex number as follows:

Def. e ^z. The Maclaurin series expansion of e^x when x is a real number is

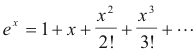
We take this Maclaurin series expansion of e^x , x real, as our definition of e^z when z is a complex number. Thus the definition of e^z for complex argument z is

Substituting the complex number z into the right member of 2) gives us a complex number which is, by definition, the value of e^z.

Def. a^z, a is real and positive. By definition, for real and positive a,

3) a^z = e ^{z ln a}

where ln a is the natural logarithm of a. Thus we evaluate a^z by substituting “z ln a” into 2) above. The motivation for this definition comes from the fact that 3) holds for the case when z is a real number.

Def. a^z, a and z both complex. By definition, if a and z are both complex,

a^z = e ^{z ln a} .

We evaluate a^z by substituting “z ln a” into 2) above.

If f(z) and g(z) are two given functions, then f(z)^g(z)= e^{g(z) ln f(z)}.

Complex exponential functions have properties similar to real exponential functions. For example:

The trigonometric functions sin z, cos z, tan z, cot z, sec z, csc z. . We must define just what we mean by the sine, cosine, tangent etc. of a complex number. There is no obvious answer. And we are not free to make just any definition we wish. We do have certain requirements that we want met. We wish to find a definition that gives, for that subset of complex numbers that are real, the same results that we get for trigonometric functions of real numbers.

Def. sin z; z complex. For a real variable x, the value of sin x is given by its Maclaurin series expansion

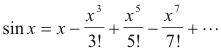
This Maclaurin series expansion that holds for the case of real arguments is used to provide a definition for the sin of a complex number. We define sin z, where z is complex, to be

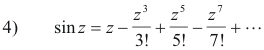
The value of sin z is, by definition, the complex number we obtain when we substitute z into the right member of 4). There is no physical interpretation or meaning for the sine of a complex number as there is for the sine of a real number. It is simply a value established by an infinite series.

Def. cos z; z complex. For a real variable x, the value of cos x is given by its Maclaurin series expansion

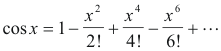
This Maclaurin series expansion is used to define the cosine of a complex number. By definition, cos z, where z is complex, is given by

The value of cos z is, by definition, the complex number we obtain when we substitute z into the right member of 5).

Def. tan z, cot z, sec z, csc z. Tan z, cot z, sec z, and csc z are defined as follows:

tan z = sin z /cos z

cot z = 1/tan z

sec z = 1/cos z

csc z = 1/sin z

Once we have defined all the common elementary functions e^x, log x, sin x, cos x, etc. for the case of complex arguments we then need to ask the following question: What are the properties of these new functions we have defined? What laws obtain for them? For complex arguments w and z, does e^we^z = e^w+z as in the case of real arguments? In the case of the trigonometric functions do all the identities and relationships that hold in the case of real arguments also hold in the case of complex arguments? If not, what laws do hold for them?

Many of the laws that hold for trigonometric functions of a real variable also hold for trigonometric functions of a complex variable. Following are some of the properties that hold:

sin² z + cos² z = 1

1 + tan² z = sec² z

1 + cot² z = csc² z

sin (-z) = -sin z

cos (-z) = cos z

tan (-z) = - tan z

sin (z₁ z₂) = sin z₁ cos z₂ cos z₁ sin z₂

cos (z₁ z₂) = cos z₁ cos z₂ sin z₁ sin z₂

Relations between the exponential and trigonometric functions. Using the Maclaurin series definitions of e^z, sin z, and cos z we can easily derive the following important theorems.

Theorem 1. For a complex variable z

6) e^iz = cos z + i sin z

7) e^-iz = cos z - i sin z

Proof

Theorem 2. For a real variable x

10) e^ix = cos x + i sin x

11) e^-ix = cos x - i sin x

We note that the set of formulas in Theorem 2 is identical to those in Theorem 1. The only difference is that in Theorem 1 the argument is the complex variable z and in Theorem 2 it is the real variable x. In fact, the formulas of Theorem 2 are simply a special case of those of Theorem 1 for if, in Theorem 1, we let z = x where x is a real number, i.e. z = x + 0i, we obtain the formulas of Theorem 2. However, we list both of these sets of formulas separately because both forms are found in the literature and both are important. These formulas are referred to as Euler’s Formulas.

Theorem 3. For a complex variable z = x + i y

14) e^z = e ^{x + iy} = e^x(cos y + i sin y)

Proof

Other useful formulas

For a real number x

obtained by substituting z = ix in 8) and 9) above.

For a complex variable z = x + iy

Proof

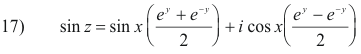
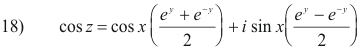
Using the polar form z = r(cos θ + i sin θ) and 10) above we have

19) z = re^iθ

The hyperbolic functions sinh z, cosh z, tanh z, coth z, sech z, csch z .

Def. sinh z; z complex. For the real variable x, the value of sinh x is given by the Maclaurin series expansion

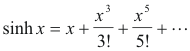
This Maclaurin series expansion is used to define the hyperbolic sine of a complex number. By definition, sinh z, where z is complex, is given by

The value of sinh z is, by definition, the complex number we obtain when we substitute z into the right member of 20).

Def. cosh z; z complex. For the real variable x, the value of cosh x is given by the Maclaurin series expansion

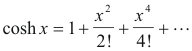
This Maclaurin series expansion is used to define the hyperbolic cosine of a complex number. By definition, cosh z, where z is complex, is given by

The value of sinh z is, by definition, the complex number we obtain when we substitute z into the right member of 21).

Def. tanh z, coth z, sech z, csch z. tanh z, coth z, sech z, and csch z are defined as follows:

tanh x = sinh x/cosh x

coth x = 1/tanh x

sech x = 1/cosh x

csch x = 1/sinh x

The following properties hold:

cosh² z - sinh² z = 1

1 - tanh² z = sech² z

coth² z - 1 = csch² z

sinh (-z) = -sinh z

cosh (-z) = cosh z

tanh (-z) = - tanh z

sinh (z₁ z₂) = sinh z₁ cosh z₂ cosh z₁ sinh z₂

cosh (z₁ z₂) = cosh z₁ cosh z₂ sinh z₁ sinh z₂

The logarithmic functions log z, ln z; z, complex. The logarithmic function log_az, z complex, is defined as the inverse of the function a^z . More specifically, if

z = a^w

then

w = log_a z .

The number w is the logarithm of z to base e if z = e^w. If we write z in the form

z = x + iy = r(cos θ + i sin θ) = re^iθ = re^i(θ+2kπ)

then

w = ln z = ln r + i(θ 2kπ)

where k = 0, 1, 2, ...

We note that ln z is a multiple-valued function.

If z = a^w then, by definition, z = e ^{w ln a}. Thus w = (ln z)/(ln a).

Inverse trigonometric functions. If z = sin w, then w = sin^-1 z is called the inverse sine of z (or arc sine of z). Similarly for the other inverse trigonometric functions cos^-1, tan^-1, etc. The inverse functions are multiple-valued. They can be expressed in terms of natural logarithms as follows. In all cases we have omitted an additive constant 2kπi, k = 0, 1, 2, ..., in the logarithm.

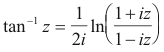
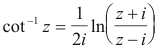
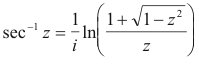
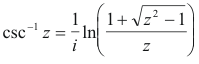
Inverse hyperbolic functions. If z = sinh w, then w = sinh^-1 z is called the inverse hyperbolic sine of z. Similarly for the other inverse hyperbolic functions cos^-1, tan^-1, etc. The inverse functions are multiple-valued. They can be expressed in terms of natural logarithms as follows. In all cases we have omitted an additive constant 2kπi, k = 0, 1, 2, ..., in the logarithm.

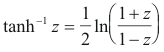
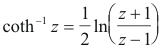
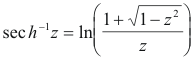
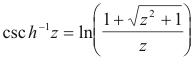
Let us now observe that what we have done above is to define the functions e^z, sin z, cos z, sinh z and cosh z in terms of their Maclaurin series expansions (expansions which are, in all cases, convergent on the entire complex plane) and then define all other functions in terms of these. Some authors define only e^z in terms of its Maclaurin series expansion and then define all other functions in terms of it. I prefer my way because I feel it makes the defining process more straightforward and transparent, less confusing, clearer. The logical structure of what has been done is simpler and clearer.

References

Mathematics, Its Content, Methods and Meaning

James and James. Mathematics Dictionary

Spiegel. Complex Variables (Schaum)