Website owner:  James Miller

THE EXPONENTIAL AND LOGARITHMIC FUNCTIONS, LOGARITHMIC DIFFERENTIATION

Exponents. The process of defining the meaning of aⁿ is a multi-step process.

 Step 1. Define the meaning of the symbol aⁿ where a is any real number and n is a positive integer as follows:

            a¹ = a

            a² = a • a

            a³ = a • a • a

            .....

            aⁿ = a • a • a .... to n factors

This gives us a meaning for aⁿ when the exponent n is a positive integer. The following laws are valid for aⁿ defined as above (m and n are positive integers):

Next we want to give a meaning to such symbols as

Our object will be to define these symbols in such a way that laws 1 through 5 will apply in all cases.

Step 2. Assign a meaning to a⁰. If we want Law 1 to hold so that

we must assign the value one to the symbol a⁰.

Def. a⁰ = 1.

Step 3. Assign a meaning to negative integral exponents. If we wish Law 1 to hold so that

            a^m • a ^{- m} = a^{m - m} = a⁰ = 1           (m is an integer, a≠0)

we must agree that a ^{- m} = 1/a^m.

Def. a^-m = 1/a^m where m is an integer.

Def. n-th root. If aⁿ = p, where n is a positive integer, we call a an n-th root of p, written There may be more than one real n-th root of p. For example since 2² = 4 and (-2)² = 4, there are two real square roots of 4, namely 2 and -2.

Step 4. Assign a meaning to fractional exponents. If we wish Law 1 to hold so that

we must define the symbol a^½ to stand for a square root of a. To avoid ambiguity we can define it to stand for the positive square root. In general, we define the symbol

to stand for the positive q-th root of a.

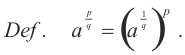
It follows from these definitions that

and that the above five laws are valid if m and n are either fractions or integers (i.e. if they are rational numbers), provided a and b are positive numbers. If the exponent is irrational, the power is defined to be the quantity approximated by using rational exponents which approximate the irrational exponent; e.g. 3 with exponent denotes the limit of the sequence

Three important limits.

Theorem 1. If θ is in radians, then

Theorem 2. If θ is in radians, then

Theorem 3. The number e is given by

Logarithms to the base e are called natural logarithms. Log_e x is often called log x (base omitted) or ln x.

Def. Exponential function. (1) The function e^x.

(2) The function a^x, where a is a positive constant. If a 1, the function a^x is the inverse of the logarithmic function log_ax.

                                                James & James. Mathematics Dictionary.

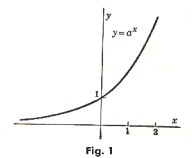
The exponential function y = a^x is shown in Fig. 1. Its derivative is everywhere positive and increases with increasing values of x.

Def. Logarithmic function y = log_a x (a > 1). The logarithmic function is defined as the inverse of the exponential function i.e. if

            x = a^y 

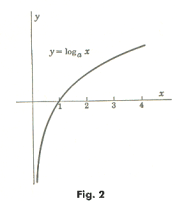
then

            y = log_a x .

See Fig. 2. Its graph is the same as that of y = a^x with the axes interchanged. It is defined only for positive values of x.

The derivative of log_a u.

Theorem.

Proof. We wish to find the derivative of the function

            y = log_a x .

We proceed by applying the fundamental differentiation process. Starting at any point P on the curve and letting x increase by an amount Δx we have

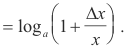
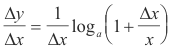
 Let us now multiply numerator and denominator by x giving

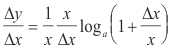
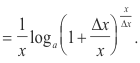
If now Δx 0, the quantity

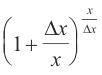
approaches the number e because it is of the form

with v approaching zero. We have then

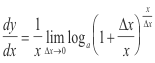
End of proof.

For the special case of natural logarithms where a = e this becomes

If we consider the function y = log_a u where u is a differentiable function of x, its derivative with respect to x is given by

For the special case of natural logarithms this becomes

Example. Find dy/dx for

Solution.

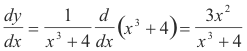
The derivative of a^u.

Theorem.

Proof. If

            y = a^x

then

            x = log_a y .

Taking the derivative with respect to y

or

            = y log_e a

            = a^x log_e a 

End of proof.

If u is a differentiable function of x we have

If a is the number e, we have

Example. Find dy/dx for

Solution.

Logarithmic differentiation. In obtaining the derivatives of certain kinds of functions, such as complicated products and quotients, and functions of the type u^v, where u and v are both variable, it is often easier to take the logarithm before differentiating. This process is called logarithmic differentiation. 

Example 1. Find dy/dx if

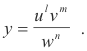
Solution. Taking logarithms of both sides

            ln y = l ln u + m ln v - n ln w

Differentiating with respect to x

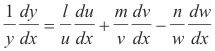
Solving for dy/dx

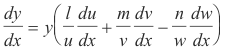
Example 2. Find dy/dx if

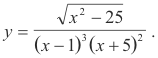
Solution. Taking logarithms of both sides

Differentiating with respect to x

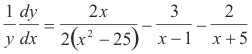
Solving for dy/dx

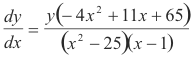
The derivative of u^v. The derivative of a function of the form

            y = u^v,

where u and v are differentiable functions of x, can be found by the method of logarithmic differentiation.

Example. Differentiate y = (x + 1)^x.

Solution. Taking the natural logarithm of each side, we obtain

            ln y = x ln (x + 1).

Now differentiating this relation implicitly with respect to x we have

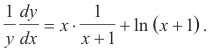
Solving for dy/dx we get

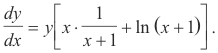
Note that neither the formula for the derivative of uⁿ nor the derivative for a^v applies to functions of this type.