Website owner: James Miller
Plane Geometry. Definitions, axioms, postulates, theorems. Straight, complementary, right, vertical, acute, obtuse angles. Equilateral, isosceles, scalene, right, acute, obtuse triangle. Quadrilateral, parallelogram, rhombus, trapezoid. Transversal. Arc, chord of a circle.
DEFINITIONS.
Proposition. A general statement concerning geometric relationships.
Postulate. A proposition that we accept without deductive reasoning.
Theorem. A proposition that we establish by means of deductive reasoning.
Angle. The inclination of one line with respect to the other of two straight lines drawn from a point. The point is called the vertex of the angle.
Right angle. An angle of 90 degrees.
Straight angle. An angle of 180 degrees.
Supplementary angles. Two angles whose sum is 180 degrees.
Complementary angles. Two angles whose sum is 90 degrees.
Adjacent angles. Two angles that have the same vertex and a common side between them.
Vertical angles. The opposite angles formed by two intersecting straight lines.
Acute angle. An angle less than a right angle.
Obtuse angle. An angle greater than a right angle but less than a straight angle.

Polygon. A closed plane figure bounded by straight lines.
Vertex of a polygon. The point where two sides of a polygon meet.
Triangle. A three-sided polygon.
Quadrilateral. A four-sided polygon.
Equilateral triangle. A triangle with three equal sides.
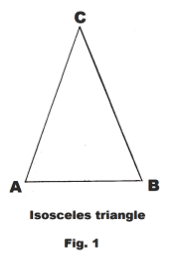
Isosceles triangle. A triangle with two equal sides. The equal sides are called the legs. The third side is called the base. The angle opposite the base is called the vertex angle and the angles that have the base as one of their sides are called the base angles. See Fig. 1. AB is the base and ∠C is the vertex angle.
Scalene triangle. A triangle with no two sides equal.
Right triangle. A triangle one of whose angles is a right angle.
Obtuse triangle. A triangle one of whose angles is an obtuse angle.
Acute triangle. A triangle all of whose angles are acute.
Parallelogram. A quadrilateral with its opposite sides parallel.
Rectangle. A parallelogram with one right angle.
Rhombus. A parallelogram with two adjacent sides equal.
Square. A rectangle with two adjacent sides equal.
Trapezoid. A quadrilateral with two and only two sides parallel.
Isosceles trapezoid. A trapezoid whose nonparallel sides are equal.
Perpendicular lines. Lines that meet each other and form right angles.
Perpendicular bisector of a line. A line which not only bisects the line but is perpendicular to it.
Altitude of a triangle. A line from any one vertex of the triangle, perpendicular to the opposite side, and terminated by that side.
Median of a triangle. A line drawn from any vertex to the middle point of the opposite side.
Orthocenter of a triangle. The point of intersection of the altitudes of the triangle.
Circumcenter of a triangle. The point of intersection of the perpendicular bisectors of the sides of the triangle.
Incenter of a triangle. The point of intersection of the bisectors of the angles of the triangle.
Median of a trapezoid. A line joining the middle points of the nonparallel sides of the trapezoid.
Transversal. A line which intersects two or more lines.
Angles formed by a transversal. When two straight lines are cut by a transversal, angles
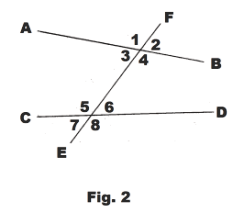
between the two lines and on opposite sides of the transversal are called alternate interior angles. Angles outside the two lines and on opposite sides of the transversal are called alternate exterior angles. Angles on the same side of the transversal and on the same side of the lines cut by the transversal are called corresponding angles. In Fig. 2, ∠5 and ∠4 are alternate interior angles, ∠7 and ∠2 are alternate exterior angles, and ∠5 and ∠1 are corresponding angles.
Circle. A closed curve all points of which are in the same plane and are equally distant from a point within it called the center.
Radius of a circle. A line from the center of the circle to any point on the circle.
Diameter of a circle. A straight line through the center of the circle with its ends on the circle.
Arc of a circle. Any part of the line forming the circle.
Semicircle. Half a circle.
Concentric circles. Two or more circles having the same center but different radii.
Minor arc of a circle. An arc that is less than a semicircle.
Chord. A line joining any two points on a circle.
Central angle of a circle. An angle with its vertex at the center of the circle and with radii for its sides.
Polygon inscribed in a circle. A polygon is said to be inscribed in a circle if all its vertices lie on the circle. In this case, the circle is said to be circumscribed about the polygon.
Tangent to a circle. A line touching a circle at only one point is called a tangent to the circle.
Common tangents. A line tangent to each of two circles is called a common tangent. If the circles lie on opposite sides of the tangent, it is a common internal tangent. If the circles lie on the same side of the tangent, it is a common external tangent.
Polygon circumscribed about a circle. A polygon is said to be circumscribed about a circle if all its sides are tangent to the circle. In this case the circle is inscribed in the polygon.
Line of centers of two circles. The line joining their centers.
Tangent circles. Two circles are said to be tangent to each other if they are both tangent to the same line at the same point. They are tangent internally if one circle lies within the other. They are tangent externally if each circle lies outside the other.
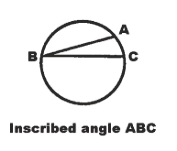
Inscribed angle; angle inscribed in a circle. An angle whose vertex is on a circle and whose sides are chords of the circle. See figure.
Angle inscribed in an arc. An angle is inscribed in an arc if the vertex is on the arc and its sides meet the extremities of the arc.
Secant. A line that intersects a circle at two points.
Proportions. An equation that states that two ratios are equal is called a proportion. In the proportion a/b = c/d a, b, c, and d are respectively the first, second, third and fourth terms. The first and fourth terms, a and d, are called the extremes and the second and third terms, b and c, the means, of the proportion.
Congruent figures. Any two geometric figures that can be made to exactly coincide (fit exactly on each other).
Similar polygons. Polygons whose corresponding angles are equal and whose corresponding sides are in proportion.
Equal figures. Figures that have the same area.
Center of a regular polygon. The common center of its inscribed and circumscribed circles.
Radius of a regular polygon. The radius of its circumscribed circle.
Apothem of a regular polygon. The apothem of a regular polygon is the radius of its inscribed circle drawn to the point of contact.
Central angle of a regular polygon. The angle between the radii drawn to adjacent vertices of the polygon.
Sector of a circle. The portion of a circle bounded by two radii and their intercepted arc.
Segment of a circle. The region of a circle bounded by a chord and its arc. If the arc is a minor arc, the segment is a minor segment; if the arc is a major arc, the segment is a major segment.
Locus of points. The set of all points that satisfy one or more given conditions. A locus may consist of points, lines or surfaces. Example. The locus of all points located at a distance r from a point A is a circle centered at A and of radius r. (If we are talking about three dimensional space, the locus of all points located at a distance r from a point A is a sphere centered at A and of radius r).
________________________________________________________________________
AXIOMS OF EQUALITY
1. Things equal to the same or equal things are equal to each other.
2. A quantity may be substituted for its equal in any expression or equation.
3. The whole equals the sum of its parts.
4. Any quantity equals itself.
5. If equals are added to equals, the sums are equal.
6. If equals are subtracted from equals, the differences are equal.
7. If equals are multiplied by equals, the products are equal.
8. If equals are divided by equals, the quotients are equal.
________________________________________________________________________
POSTULATES.
1. Two triangles are congruent if two sides and the included angle of one are equal to two sides and the included angle of the other (i.e. s.a.s. = s.a.s.).
2. Two triangles are congruent if two angles and the included side of one are equal to two angles and the included side of the other (i.e. a.s.a. = a.s.a.).
3. Two triangles are congruent if three sides of one are equal to three sides of the other (i.e. s.s.s. = s.s.s.).
4. All right angles are equal.
5. All straight angles are equal.
6. A straight line can be extended in either direction to any desired length.
7. Two straight lines cannot intersect in more than one point.
8. Through two given points one and only one straight line can be drawn.
9. A straight line is the shortest line that can be drawn between two points.
10. One and only one circle can be drawn with any point as center and any line segment as radius.
11. At a point on a line or from a point outside a line only one perpendicular can be drawn to the line.
12. The shortest distance from a point to a line is the perpendicular from the point to the line.
13. An angle has only one bisector.
14. A line has only one midpoint.
15. If two right triangles have the hypotenuse and an acute angle of one equal to the hypotenuse and an acute angle of the other, they are congruent.
16. Through a given point not on a given line, one and only one line can be drawn parallel to the given line.
17. Two lines perpendicular to a third line all in the same plane are parallel.
18. Two circles are equal if their radii or their diameters are equal.
19. A diameter bisects a circle.
20. If a line bisects a circle and is terminated the circle, it is a diameter.
21. A straight line cannot intersect a circle in more than two points.
22. If the distance from a point to the center of a circle is equal to a radius, the point lies on the circle. If the distance from a point to the center of a circle is greater than a radius, the point lies outside the circle. If the distance from a point to the center of a circle is less than a radius, the point lies within the circle.
23. In the same circle or in equal circles, equal central angles have equal arcs.
24. In the same circle or in equal circles, equal arcs have equal central angles.
25. A straight line perpendicular to a radius at its outer extremity is tangent to the circle.
26. A tangent to a circle is perpendicular to the radius drawn to the point of contact.
27. A line perpendicular to a tangent at its point of contact passes through the center of the circle.
28. A line from the center of a circle and perpendicular to a tangent passes through the point of contact.
29. A central angle has the same number of degrees as its intercepted arc.
30. A line parallel to one side of a triangle and intersecting the other two sides divides them into segments which, taken in the same order, have the same ratio.
31. The area of a rectangle is equal to the product of its base and altitude.
32. If one straight line meets another so as to form adjacent angles, the angles are supplementary.
33. If two adjacent angles form a right angle, the angles are complementary.
34. If two angles are supplementary to the same angle or to equal angles, they are equal.
35. If two angles are complementary to the same angle or to equal angles, they are equal.
36. If two straight lines intersect, the vertical angles are equal.
37. In the same circle or in equal circles, the larger of two central angles has the longer arc.
38. In the same circle or in equal circles, the larger of two minor arcs has the larger central angle.
39. Three parallel lines cut off on any two transversals segments which taken in the same order have the same ratio.
40. A line parallel to one side of a triangle divides the other two sides so that either side is to one of its segments as the other is to the corresponding segment.
41. Corresponding angles of similar polygons are equal.
42. Corresponding sides of similar polygons are in proportion.
43. Two polygons are equal if they are composed of respectively congruent parts.
Note. Some of these postulates can be deduced from others and could be listed as theorems. We don’t wish here to present an irreducible set of postulates. Note that the above postulates constitute assertions which one could call “statements of the obvious”. In Euclidean geometry we start with assertions that are “statements of the obvious” and then proceed to deduce, in the form of theorems, conclusions that are not obvious.
________________________________________________________________________
GENERAL THEOREMS
1.0 If two sides of a triangle are equal, the angles opposite those sides are equal.
1.1 An equilateral triangle is also equiangular.
2.0 If two angles of a triangle are equal, the sides opposite those angles are equal.
2.1 An equiangular triangle is also equilateral.
3.0 The bisector of the vertex angle of an isosceles triangle bisects the base and is perpendicular to it.
4.0 The line that connects the vertex of an isosceles triangle with the middle point of the base bisects the vertex angle and is perpendicular to the base.
5.0 If lines are drawn from any point on the perpendicular bisector of a line to the extremities of the line, they are equal.
6.0 Two points each equally distant from the extremities of a line determine the perpendicular bisector of the line.
7.0 If two right triangles have the hypotenuse and another side of one equal to the hypotenuse and a side of the other, they are congruent.
8.0 If two straight lines are cut by a transversal so that two alternate interior angles are equal, the lines are parallel.
9.0 If two straight lines are cut by a transversal so that two corresponding angles are equal, the lines are parallel.
10.0 If two straight lines are cut by a transversal so that two interior angles on the same side of the transversal are supplementary, the lines are parallel.
11.0 If a line is perpendicular to one of two parallel lines, it is perpendicular to the other also.
12.0 If two parallel lines are cut by a transversal, the alternate interior angles are equal.
13.0 If two parallel lines are cut by a transversal, the corresponding angles are equal.
14.0 If two parallel lines are cut by a transversal, the interior angles on the same side of the transversal are supplementary.
15.0 Two straight lines parallel to the same straight line are parallel to each other.
16.0 The sum of the angles of a triangle is 180 degrees.
16.1 If two angles of one triangle are equal to two angles of another triangle, the third angles are equal.
16.2 A triangle can have but one right angle or one obtuse angle.
16.3 If two right triangles have an acute angle of one equal to an acute angle of the other, the other acute angles are equal.
16.4 The acute angles of a right triangle are complementary.
16.5 Each angle of an equilateral triangle is 60 degrees.
16.6 If two triangles have two angles and a side of one equal respectively to two angles and the corresponding side of the other, they are congruent.
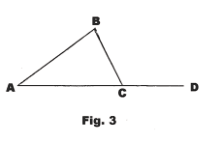
16.7 If one side of a triangle is extended, the exterior angle thus formed is equal to the sum of the two remote interior angles.
Example. In Fig. 3, ∠BCD is the exterior angle formed and ∠A and ∠B are the remote interior angles. Thus ∠BCD = ∠A + ∠B.
17.0 The sum of the angles of a polygon of n sides is (n-2)180 degrees.
17.1 The sum of the exterior angles of a polygon made by extending each of its sides in succession is equal to 360 degrees. See Fig. 4
The sum of the interior angles of a polygon is a variable and depends on the number of sides of
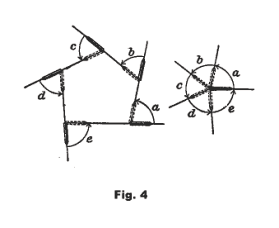
the polygon. However, the sum of the exterior angles of a polygon is a constant.
18.0 The opposite sides of a parallelogram are equal.
18.1 The opposite angles of a parallelogram are equal.
18.2 A diagonal of a parallelogram divides it into two congruent
triangles.
18.3 Parallel lines are at all points the same distance apart.
18.4 The successive angles of a parallelogram are supplementary.
19.0 The diagonals of a parallelogram bisect each other.
20.0 If the opposite sides of a quadrilateral are equal, the figure is a parallelogram.
21.0 If two sides of a quadrilateral are parallel and equal, the figure is a parallelogram.
22.0 If the diagonals of a quadrilateral bisect each other, the figure is a parallelogram.
22.1 Each angle of a rectangle is a right angle.
22.2 The diagonals of a rectangle are equal.
22.3 If the diagonals of a parallelogram are equal, it is a rectangle.
22.4 The diagonals of a rhombus are perpendicular to each other.
22.5 The diagonals of a rhombus bisect its angles.
22.6 If the diagonals of a parallelogram are perpendicular to each other, it is a rhombus.
23.0 If a line joins the middle points of two sides of a triangle, it is parallel to the third side and equal to half of it.
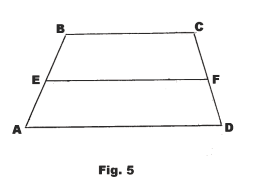
24.0 The median of a trapezoid is parallel to the bases and equal to one half their sum. See Fig. 5.
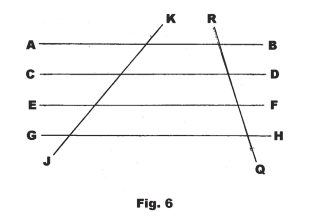
25.0 If three or more parallel lines cut off equal segments on one transversal, they cut off equal segments on every transversal.
Given that the four parallel lines of Fig. 6 cut off equal segments on transversal JK. Then they cut off equal segments on every tranversal QR.
25.1 If a line is parallel to one side of a triangle and bisects another side, it bisects the third side also.
25.2 If a line is parallel to the bases of a trapezoid and bisects one of the nonparallel sides, it bisects the other also.
26.0 In the same circle or in equal circles, equal chords have equal arcs.
27.0 In the same circle or in equal circles, equal arcs have equal chords.
28.0 If a line through the center of a circle is perpendicular to a chord, it bisects the chord and its arc.
28.1 A line through the center of a circle that bisects a chord (not a diameter) is perpendicular to it.
29.0 In the same circle or in equal circles, equal chords are equally distant from the center.
30.0 In the same circle or in equal circles, chords equally distant from the center are equal.
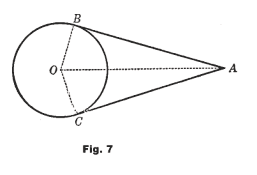
31.0 The tangents to a circle from a point outside the circle are equal.
31.1 If two tangents are drawn to a circle from an outside point, the line from the point to the center bisects the angle between the tangents. See Fig.7.
32.0 If two circles are tangent to each other, their line of centers passes through the point of contact.
33.0 If two sides of a triangle are unequal, the angles opposite those sides are unequal in the same order.
34.0 If two angles of a triangle are unequal, the sides opposite those sides are unequal in the same order.
35.0 If two sides of one triangle are equal to two sides of another triangle and the included angle of the first is greater than the included angle of the second, then the third side of the first is greater than the third side of the second.
36.0 If two triangles have two sides of one equal to two sides of the other and the third side of the first is greater than the third side of the second, then the angle opposite the third side of the first is greater than the angle opposite the third side of the second.
37.0 In the same circle or in equal circles, the longer of two minor arcs has the longer chord.
38.0 In the same circle or in equal circles, the longer of two chords has the longer minor arc.
39.0 In the same circle or in equal circles, unequal chords are unequally distant from the center, the longer chord being the nearer.
40.0 In the same circle or in equal circles, chords unequally distant from the center are unequal, the nearer being the longer.
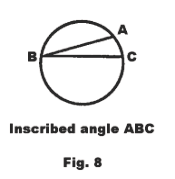
41.0 An inscribed angle has half as many degrees as the intercepted arc. See Fig. 8. ∠B has half as many degrees as arc AC.
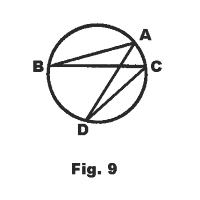
41.1 Angles inscribed in the same arc are equal.
Example. In Fig. 9, ∠B and ∠D are both inscribed in arc ABDC. Thus ∠B = ∠D .
41.2 An angle inscribed in a semicircle is a right angle.
42.0 An angle formed by a tangent and a chord meeting it at the point of contact has half as many degrees as the intercepted arc.
Example. In Fig. 10, ∠ABC is formed by tangent EBC meeting chord AB at point of contact B. If arc AB = ao, then ∠ABC = ao,/2.
43.0 An angle formed by two chords intersecting within a circle has half as many degrees as the
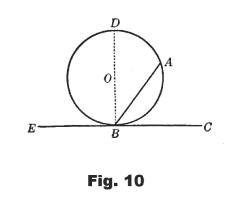
sum of the two arcs intercepted by it and by the vertical angle.
In Fig. 11, ∠AEB is formed by intersecting chords AC and BD. If arc AB = ao and arc DC = bo, then ∠AEB = (ao + bo) /2.
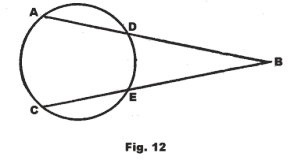
44.0 An angle formed by two secants intersecting outside a circle has half as many degrees as the difference between the two intercepted arcs.
See Fig. 12. Given a circle with secants BDA and BEC. If arc AC = ao and arc DE = bo, then ∠B = (ao - bo) /2.
44.1 The angle formed by a secant and a tangent or two tangents meeting outside the circle has half as many degrees as the difference between the two intercepted arcs.
45.0 Parallel lines intercept equal arcs on a circle.
46.0 The opposite angles of an inscribed quadrilateral are supplementary.
47.0 If a circle is divided into any number of equal arcs, the chords of these arcs form a regular polygon of that number of sides.
47.1 An equilateral polygon inscribed in a circle is a regular polygon.
47.2 A regular quadrilateral is a square.
47.3 The side of a regular hexagon inscribed in a circle is equal to the radius of the circle.
47.4 Chords joining the alternate vertices of a regular inscribed hexagon form an equilateral triangle.
________________________________________________________________________
LOCUS THEOREMS
1.0 The locus of a point at a given distance from a given point is a circle with the point as center and the given distance as radius.
2.0 The locus of a point at a given distance from a given line is a pair of lines, one on each side of the given line, parallel to it at the given distance from it.
3.0 The locus of a point equally distant from two parallel lines is a line parallel to them and midway between them.
4.0 The locus of a point equally distant from two points is the perpendicular bisector of the line joining the two points.
4.1 The perpendicular bisector of a chord passes through the center of the circle.
5.0 The locus of a point equally distant from the sides of an angle is the bisector of the angle.
6.0 The locus of the vertex of the right angle with a fixed hypotenuse is a circle whose diameter is the hypotenuse.
________________________________________________________________________
48.0 The perpendicular bisectors of the sides of a triangle meet at a point which is equally distant from the vertices of the triangle.
49.0 The bisectors of the angles of a triangle meet at a point that is equally distant from the sides of the triangle.
________________________________________________________________________
Locus theorem
7.0 The locus of the vertex of a triangle having a fixed base and a given vertex angle is the arc of a circle drawn to (passing through) the extremities of the base and passing through any one position of the vertex.
________________________________________________________________________
50.0 The altitudes of a triangle meet at a point.
51.0 The medians of a triangle meet at a point which is two thirds of the distance from each
vertex to the midpoint of the opposite side.
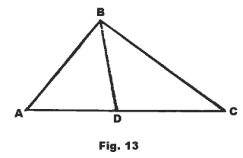
52.0 The bisector of an angle of a triangle divides the opposite side into segments which have the same ratio as the other two sides.
In Fig. 13, if BD bisects ∠B, then AD/DC = AB/BC.
________________________________________________________________________
PROPORTION THEOREMS
1.0 In any proportion, the product of the extremes is equal to the product of the means. Thus if a/b = c/d, then ad = bc.
2.0 If the product of two numbers is equal to the product of two other numbers, either pair may be made the means and the other pair the extremes of a proportion. Thus if ad = bc, then a/b = c/d, b/a = d/c.
3.0 If the numerators of a proportion are equal, the denominators are equal. If the denominators are equal, the numerators are equal.
4.0 The terms of a proportion are also in proportion by inversion; that is, the second term is to the first as the fourth is to the third. Thus if a/b = c/d, then b/a = d/c.
5.0 The terms of a proportion are also in proportion by alternation; that is, the first term is to the third as the second is to the fourth. Thus if a/b = c/d, then a/c = b/d.
6.0 The terms of a proportion are also in proportion by addition; that is, the sum of the first and second terms is to the second term as the sum of the third and fourth is to the fourth. Thus if a/b = c/d, then (a+b)/b = (c+d)/d.
7.0 The terms of a proportion are also in proportion by subtraction; that is, the first term minus the second is to the second as the third term minus the fourth is to the fourth. Thus if a/b = c/d, then (a-b)/b = (c-d)/d.
8.0 If three terms of one proportion are equal respectively to the three corresponding terms of another proportion, then the remaining term of the first is equal to the remaining term of the second. Thus if a/b = x/c and a/b = y/c, then x = y.
________________________________________________________________________
53.0 If a line divides two sides of a triangle proportionally, it is parallel to the third side.
53.1 If a line divides two sides of a triangle so that either side is to one of its segments as the other side is to the corresponding segment, it is parallel to the third side.
54.0 Two triangles are similar if two angles of one are equal to two angles of the other.
54.1 Two right triangles are similar if an acute angle of one is equal to an acute angle of the other.
55.0 Two triangles are similar if they have an angle of one equal to an angle of the other, and the sides including these angles are in proportion.
56.0 Two triangles are similar if their corresponding sides are in proportion.
57.0 Corresponding altitudes of similar triangles have the same ratio as any two corresponding sides.
58.0 If two chords intersect within a circle, the product of the segments of one is equal to the product of the segments of the other.
59.0 If from a point outside a circle two secants are drawn, the product of one secant and its external segment is equal to the product of the other secant and its external segment.
Referring to Fig. 12, showing a circle with secants BDA and BEC, AB×DB = CB×EB.
60.0 If from a point outside a circle a secant and a tangent are drawn, the product of the secant and its external segment is equal to the square of the tangent.
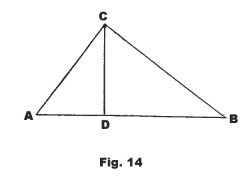
61.0 In any right triangle the altitude upon the hypotenuse is the mean proportional between the segments of the hypotenuse.
See Fig. 14. Given a right triangle ABC with right angle at C and CD ⊥ AB. Then AD/DC = DC/DB.
62.0 If the altitude upon the hypotenuse of a right triangle is drawn, either arm is the mean proportional between the whole hypotenuse and the segment of the hypotenuse adjacent to the arm.
See Fig. 14. Given a right triangle ABC with right angle at C and CD ⊥ AB. Then AB/AC = AC/AD and AB/BC = BC/DB.
63.0 In any right triangle, the square of the hypotenuse is equal to the sum of the square of the arms.
64.0 In a right triangle, if one angle is 30 degrees, the hypotenuse is twice the side opposite the 30 degree angle.
65.0 In a right triangle, if the hypotenuse is twice one of the arms the angle opposite that arm is 30 degrees.
66.0 The area of a parallelogram is equal to the product of its base and altitude.
66.1 Parallelograms with equal bases and equal altitudes are equal.
67.0 The area of a triangle is equal to one half the product of its base and altitude.
67.1 Triangles with equal bases and equal altitudes are equal.
67.2 Triangles which have equal bases in the same straight line and vertices in a line parallel to the bases are equal.
68.0 The area of a trapezoid equals one half its altitude times the sum of its bases.
69.0 The areas of two similar triangles are to each other as the squares of any two corresponding sides.
70.0 A circle can be circumscribed about any regular polygon.
71.0 A circle can be inscribed in any regular polygon.
71.1 The central angle of a regular polygon of n sides is equal to 360/n degrees.
71.2 The apothem of a regular polygon is the perpendicular bisector of its side.
71.3 The radius of a regular polygon bisects the angle to whose vertex it is drawn.
72.0 If a circle is divided into three or more equal arcs, the tangents at the points of division form a regular circumscribed polygon.
73.0 Regular polygons of the same number of sides are similar.
74.0 In a series of equal ratios the sum of the numerators is to the sum of the denominators as any numerator is to its denominator. Thus if a/b = c/d = e/f = r, then (a+c+e)/(b+d+f) = r = a/b = c/d = e/f.
75.0 The perimeters of similar polygons are to each other as any two corresponding sides.
76.0 The perimeters of two regular polygons of the same number of sides are to each other as their radii or as their apothems.
77.0 The area of a regular polygon is half the product of its apothem and its perimeter.
77.1 The areas of two regular polygons of the same number of sides are to each other as the squares of their radii or as the squares of their apothems.
78.0 The circumferences of two circles are to each other as their radii.
79.0 The areas of two circles are to each other as the squares of their radii.
References
Clark, Smith, Schorling. Modern-School Geometry.
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life