Fourier integral, transform. Magnitude and phase spectrum. Theorems. Impulse, rectangle, triangle, Heaviside unit step, sign functions. Convolution. Correlation, autocorrelation.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

The Fourier integral. Let f (t) satisfy the Dirichlet conditions

(a) it is continuous except for a finite number of discontinuities

(b) it has only a finite number of maxima and minima.

on any finite interval

and assume that the integral

exists. Then Fourier’s integral theorem states that

(This is the complex, exponential form of the Fourier integral.)

Fourier transform. If we define

equation 1) becomes

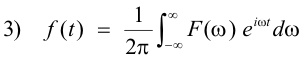
The functions f (t) and F(ω) are called a Fourier transform pair. F(ω) is the Fourier transform of f (t) and f (t) is the inverse Fourier transform of F(ω). A sufficient condition for the existence of the Fourier transform F(ω) is that

i.e. that the integral exists. This condition is not a necessary condition, however, as functions exist which don’t meet the condition but do have Fourier transforms.

Theorem 1. If f(t) is real, then Fourier’s Integral Theorem states

Magnitude spectrum and phase spectrum of a function f(t). Let F(ω) be the Fourier transform of a function f (t). The function F(ω) is, in general, complex. Let us write it as

5) F(ω) = R(ω) + i X(ω) = |F(ω)| e ^{i φ(ω)}

where |F(ω)| is called the magnitude spectrum of f (t) and φ(ω) is called the phase spectrum of f (t). Since for any complex number x + iy, x + iy = re^iθ, the magnitude spectrum is given by

and the phase spectrum is given by

General Fourier transform theorems

Theorem 2. If f (t) is real, then the real and imaginary parts of the Fourier transform F(ω) of f(t) are

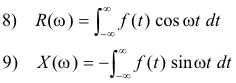
and

10) R(ω) = R(-ω)

11) X(ω) = -X(-ω)

12) F(-ω) = F*(ω)

where F*(ω) denotes the complex conjugate of F(ω).

From 10) and 11), we see that R(ω) and X(ω) are even and odd functions of ω, respectively.

From Theorem 2, we conclude:

Theorem 3. If f (t) is real, the Fourier transform F(ω) of f(t) is

where the real portion of F(ω) is an even function and the imaginary portion is an odd function.

Theorem 4. If F(ω) is the Fourier transform of f (t),

F(-ω) = F*(ω)

is a necessary and sufficient condition for f (t) to be real.

Theorem 5. Let F(ω) be the Fourier transform of f (t). If f (t) is real, its magnitude spectrum |F(ω)| is an even function of ω and its phase spectrum φ(ω) is an odd function of ω.

Theorem 6. If the Fourier transform of a real function f (t) is real, then f (t) is an even function of t, and if the Fourier transform of a real function f (t) is pure imaginary, then f (t) is an odd function of t.

Fourier sine and cosine transforms

Theorem 6. If f (t) is given only for 0 < t < ∞, f (t) can be represented by

where F_C(ω) is the Fourier cosine transform of f (t)

Procedure. If f (t) is given only for 0 < t < ∞, we can define f (t) for negative t by the equation f (-t) = f (t), so the resulting function is even. We may then utilize the Fourier cosine transform and its inverse to represent the function. In interpreting results we must, of course, remember that f (t) is defined only for t greater than zero.

Theorem 7. If f (t) is given only for 0 < t < ∞, f (t) can be represented by

where F_S(ω) is the Fourier sine transform of f (t)

Procedure. If f (t) is given only for 0 < t < ∞, we can define f (t) for negative t by the equation f (-t) = -f (t), so the resulting function is odd. We may then utilize the Fourier sine transform and its inverse to represent the function. In interpreting results we must, of course, remember that f (t) is defined only for t greater than zero.

Another form of the Fourier integral and Fourier transform

Let us make the substitution

ω = 2πs

into equation 1) above where ω represents angular velocity and s represents frequency. With this substitution, the Fourier integral theorem becomes

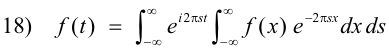
Let us now define the Fourier transform as

and 18) becomes

where F(s) and f(t) constitute a Fourier transform pair.

Fourier transform theorems

Following is a concise summary of important Fourier transform theorems.

Fourier transform. The Fourier transform of the function f(x) is F(s). We can write F[f(x)] = F(s) and F^-1[F(s)]= f(x).

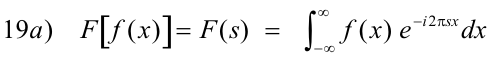
and

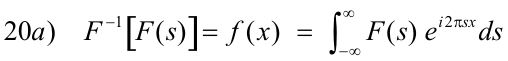
Theorem f (x) F(s)

_____________________________________________________________________________

Linearity a g(x) + b h(x) a G(x) + b H(x)

(a and b constants)

Similarity f (ax)

Shift f(x-a) F(s)e^-i2πas

Modulation f(x)cos ωx ½ F(s-[ω/2π]) +½ F(s+[ω/2π])

Convolution f(x)*g(x) F(s)G(s)

Autocorrelation f(x)*[f*(-x)] |F(s)|²

Derivative f’(x) i2πsF(s)

(providing f(x) →0 as x → + ∞)

_____________________________________________________________________________

Derivative of convolution

Rayleigh

Power

(f and g real)

_____________________________________________________________________________

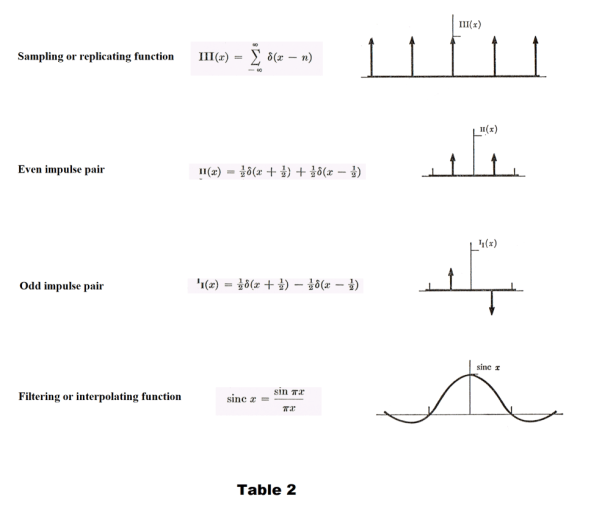
Special functions. There are a number of special functions that are widely used in Fourier analysis. The most important ones with definitions and graphs are shown in Tables 1 and 2 below.

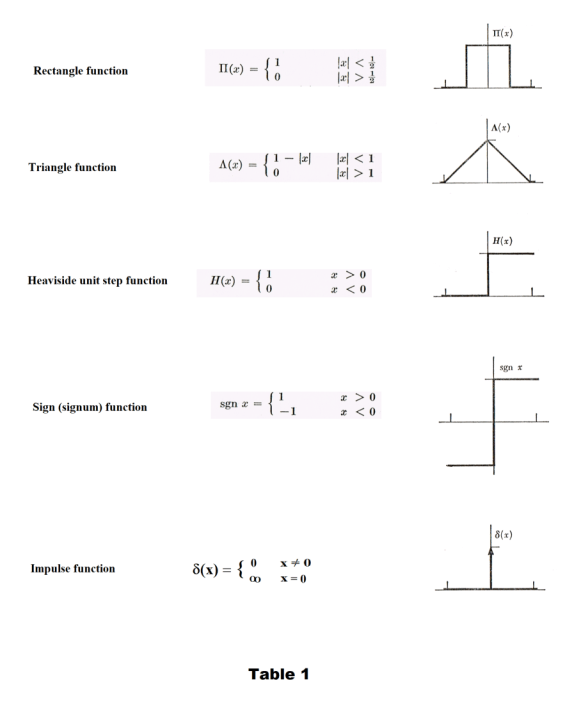
Def. Rectangle function. A function [see Fig. 1 (a)] of unit height and unit base length defined by

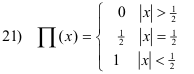
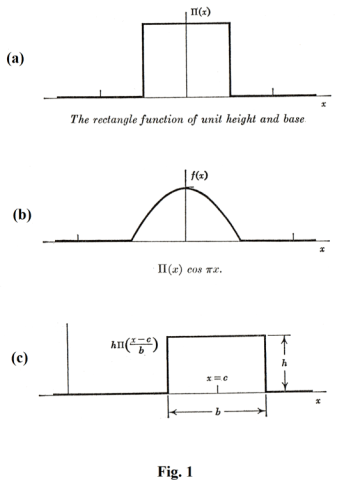
This function is used to select segments of some particular function, masking out the rest. For example, the function f(x) = II(x) cos x selects and displays the portion of the cos x function in the interval [-½, ½] and masks out the rest as shown in Fig.1 (b), providing a compact notation for

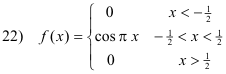
It should be noted that hII[(x - c)/b] is a displaced rectangle function of height h and base b, centered at x = c. See Fig 1 (c). Using a suitably displaced rectangle function one can select any segment of a given function, masking out the rest (i.e. reducing it to zero).

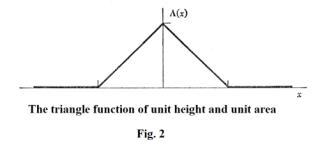
Def. Triangle function. A function defined by

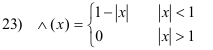
See Fig. 2. Note that h∧(x/½b) is a triangle function of height h, base b, and area ½hb. The main importance of the triangle function derives from it being the self-convolution of II(x).

Def. Heaviside’s unit step function. A function defined by

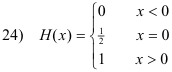
See Fig. 3 (a). As with the rectangle function, the Heaviside unit step function is used to select segments of some function, masking out the rest. The rectangle function II(x) can be expressed in terms of step functions as

25) II(x) = H(x + ½) - H(x - ½)

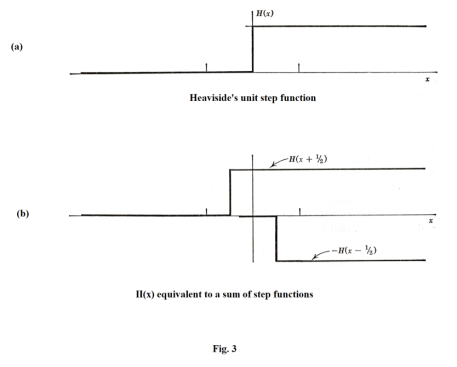
See Fig. 3(b).

Def. Sign function. The function sgn x (pronounced signum x) is equal to +1 or -1 , according to the sign of x.

Def. Impulse function (also called Delta function). The impulse function δ(x) (which is not actually a function in the usual sense of the word) has the following two properties:

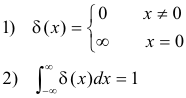
It can be defined as:

The τ^-1II(x/τ) product represents a rectangle function of height 1/τ and base τ and with unit area. As τ approaches zero a sequence of unit-area pulses of ever-increasing height are generated. The limit of the integral is, of course, equal to 1.

Fourier transform of functions built up from rectangle functions

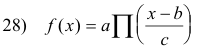
it can be shown that its transform is given by

29) F(s) = ace^-2πbssinc cs

If now we have a function built up from a sequence of rectangle functions

the transform is given by

Such functions occur frequently in engineering and can simulate, as closely as desired, any kind of variation.

Convolution of two functions. The convolution of two functions f (x) and g(x) is defined as

and denoted by f *g.

Syn. bilateral convolution

The convolution of two functions occurs widely in mathematics, science and engineering in many contexts and under various names (including the German term Faltung). One place where it occurs is in connection with data smoothing. An example involving data smoothing is shown in Fig. 4 where f(x), g(x), and h(x) are shown. The functions g(x-u) and f(u)g(x-u) are shown for one particular value of x, x= x_i. h(x_i) represents the area under f(u)g(x_i-u).

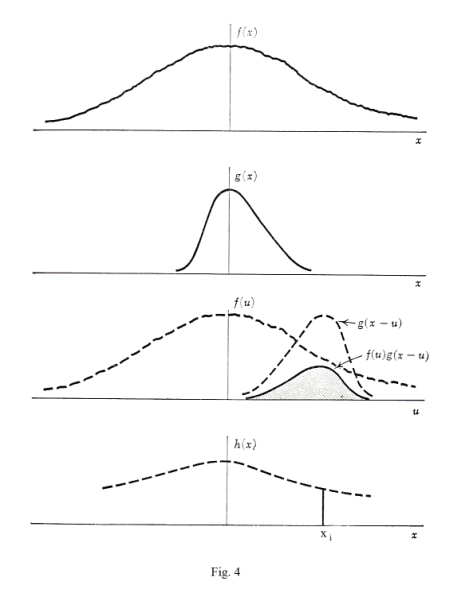
Fig. 5 shows the reason for the German term Faltung (which means “folded back”) for the convolution operation. Here g(u) is shown folded back on itself about the line u = ½x to give g(x-u). For each value of x= x_i there is a function g(x_i-u) that can be obtained by a fold at u = ½x — along with the function f(u)g(x_i-u). h(x_i) represents the area under f(u)g(x_i-u).

The Convolution theorem. The Fourier transform of the convolution of f and g is the product of the Fourier transforms of f and g i.e.

32) F (f *g) =F (f ) F(g)

Theorem 8. Convolution obeys the commutative law.

33) f(t)*g(t) = g(t)*f(t)

Theorem 9. Convolution obeys the associative law.

34) [f₁(t)*f₂(t)]*f₃(t) = f₁(t)*[f₂(t)*f₃(t)]

Theorem 10. The convolution of a function f(t) with a unit impulse function δ(t) yields the function f(t) itself.

35) f(t)*δ(t) = f(t)

Theorem 11. The following relationships hold:

36) f(t)*δ(t - T) = f(t - T)

37) f(t - t₁)*δ(t - t₂) = f(t - t₁ - t₂)

Correlation functions. In signal processing, the functions

and

(where f₁(t) and f₂(t) are real-valued functions) are known as cross-correlation functions. They represent a measure of the similarity between the two functions f₁(t) and f₂(t) as a function of the shift of one function relative to the other. If the cross-correlation function is identically zero for all τ, the two functions are said to be uncorrelated. They are commonly used for searching a long signal for a shorter, known feature. If f₁(t) and f₂(t) are identical, the correlation function

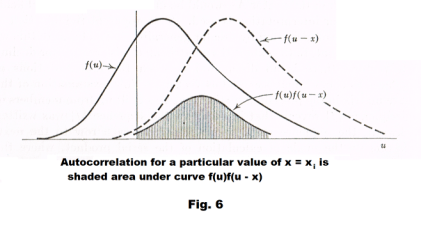
is called the autocorrelation of f₁(t). In Fig. 6. the shaded area under the curve f(u)f(u - x) represents the autocorrelation

for a particular value of x, x = x_i.

Note. The cross-correlation integral is similar to the convolution integral but has different properties. For example, in the case of convolution f₁* f₂ = f₂*f₁, whereas with cross-correlation this is not the case. When the functions are complex it is customary to define the complex cross-correlation function by

where the * denotes the conjugate.

By making a change of variable from t to t + τ, it can be readily seen that

Theorem 12. The following relationships hold:

44) R₁₂(τ) = R₂₁(-τ)

45) R₁₁(τ) = R₁₁(-τ)

Equation 45) states that the autocorrelation function is an even function of τ.

Theorem 13. If F[f₁(t)] = F₁[(s)] and F[f₂(t)] = F₂[(s)], then

46) F[R₁₂(τ)] = F₁[(s)] F₂[(-s)]

47) F[R₂₁(τ)] = F₁[(-s)] F₂[(s)]

48) F[R₁₁(τ)] = F₁[(s)] F₁[(-s)]

49) F[R₁₁(τ)] = |F₁[(s)]|² if f₁(t) is real

From 49) we see that the Fourier transform of the autocorrelation function R₁₁(τ) yields the energy spectrum |F₁[(s)]|² . Thus the autocorrelation function R₁₁(τ) and the energy spectral density |F₁[(s)]|² constitute a Fourier transform pair.

If f(t) is complex it is customary to define the complex autocorrelation of f(t) as

where the * denotes the conjugate.

References

Hsu. Fourier Analysis

Bracewell. The Fourier Transform and Its Applications

James, James. Mathematics Dictionary

Spiegal. Laplace Transforms. (Schaum) Chap. 6

Wikipedia