Concepts of Topology. Topological property. Topological transformation. Continuous deformation. Genus. Homeomorphism.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

What is the subject of topology all about? With what subject matter is it concerned? What kinds of questions does it ask? With what kinds of problems is it concerned? Let us start with some dictionary definitions.

Topology. The study of those properties of geometric figures or solid bodies that remain invariant under certain transformations.

Funk & Wagnalls Dictionary

Topology. That branch of geometry which deals with the topological properties of figures. Combinatorial topology is the branch of topology which is the study of geometric forms by decomposing them into the simplest geometric figures (simplexes) which adjoin each other in a regular fashion. Algebraic topology includes the fields of topology which use algebraic methods (especially group theory) to a large extent. Point-set topology is the study of sets as accumulations of points (as contrasted to combinatorial methods of representing an object as a union of simpler objects) and describing sets in terms of topological properties such as being open, closed, compact, normal, regular, connected, etc.

James & James. Mathematics Dictionary.

Topological property. Any property of a geometrical figure A that holds as well for every figure into which A may be transformed by a topological transformation. Examples are the properties of connectedness and compactness, of subsets being open or closed, and of points being limit points.

James & James. Mathematics Dictionary.

Def. Topological transformation. A transformation that carries a geometric figure A into another figure B is a topological transformation if the following conditions are met:

1) the transformation is one-to-one

2) the transformation is bicontinuous (i.e. continuous in both directions)

Syn. Homeomorphism

The meaning of a mapping being bicontinuous is as follows: Let T be a bicontinuous mapping of a figure A into a figure B. Then if we take any two points p and q of A and move p so that the distance between it and q approaches zero, then the distance between the corresponding points p' and q' of B will also approach zero.

One characteristic of a topological transformation carrying a geometric figure A into another figure B is that open sets in A are carried into open sets in B, and conversely open sets in B are carried into open sets in A (and analogously for closed sets).

Def. Topologically equivalent figures. If one figure can be transformed into another by a topological transformation, the two figures are said to be topologically equivalent.

Continuous deformations are examples of topological transformations.

Def. Continuous deformation. A transformation which shrinks, twists, etc. in any way without tearing.

James & James. Mathematics Dictionary.

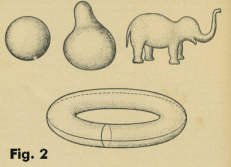
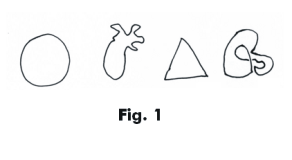
Intuitively a continuous deformation of an arbitrary figure can be thought of as follows: Envision a figure drawn on a rubber sheet. A deformation of the sheet by stretching, twisting, bending, etc. which doesn’t tear the sheet will change the figure into some other shape. All the different shapes that the figure can be changed into in this way are topologically equivalent. Or consider a rubber ring in the shape of a circle. It can be deformed into many different shapes, as shown in Fig. 1, and all the different shapes it can deformed into are topologically equivalent. Or consider a sphere made of a thin rubber sheet. It can be deformed into many shapes — an ellipsoid, a cube, a pear shape, an elephant shape — and all the different shapes it can be changed into in this manner are topologically equivalent. However, note that a sphere cannot be changed in this manner into a square or a torus (doughnut shaped surface). See Fig. 2. The sphere and the torus are topologically distinct surfaces. They belong to different topological types.

The general concept of a topological transformation is broader than that of a continuous deformation, however. For example, if a figure is cut during a deformation and the edges are sewn back together after the deformation in exactly the same way as before, the process still defines a topological transformation of the figure, although it is not a deformation. Any two “knots” formed by looping and interlacing a piece of string and then joining the ends together are topologically equivalent, but cannot necessarily be continuously deformed into each

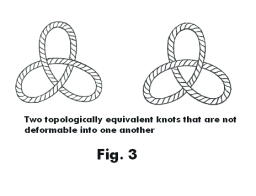
other. The two knots of Fig. 3 are topologically equivalent but cannot be deformed into one another. Thus we see that while figures or surfaces that can be continuously deformed into each other are topologically equivalent, figures or surfaces that cannot be continuously deformed into each other may still be topologically equivalent.

Properties preserved under topological transformations. Some properties are preserved under topological transformations and others are not. The property of a circle of being a simple closed curve is a property that is preserved under an arbitrary topological transformation. It is a topological property. The surface of a sphere has the following two properties that are preserved under an arbitrary topological transformation.

1. The surface is closed. There are no edges on it (as with a square).

2. Every simple closed curve on its surface represents a dissection of it in this sense: if we make a cut along the curve, the surface separates into two disconnected parts.

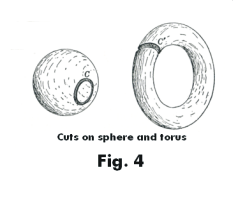
These are two topological properties of the sphere. Now let us note that the second property differentiates the sphere from the torus. If we cut a torus along a meridian then it is not split into two parts but instead is turned into a bent tube which can be turned into a cylinder by straightening. See Fig. 4.

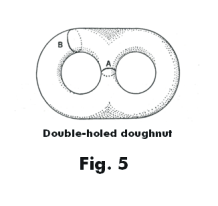
Genus of a surface. The genus of a surface is its topological type. Surfaces of the same genus are topologically equivalent to each other. Surfaces of different genuses are not topologically equivalent. What characteristic of a surface allows us to determine its genus? The characteristic is this: the largest number of non-intersecting simple closed curves that can be drawn on the surface without separating it (i.e. cause the surface to separate into disconnected parts when cuts are made along the curves). The genus of a sphere is 0 since no such curves can be drawn on its surface without separating it. The genus of a torus is 1 since one, and no more than

one, such curves can be drawn on its surface without separating it. Consider now the double-holed doughnut shown in Fig. 5. It has a genus of 2 since two, but not more, such curves can be drawn on its surface without separating it. In a similar way, a triple-holed doughnut has a genus of 3 since three, and no more, such curves can be drawn on its surface without separating it, and in general, a p-holed doughnut has a genus of p since p (and no more) such curves can be drawn on its surface without separating it.

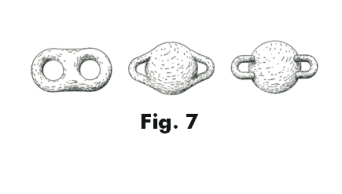
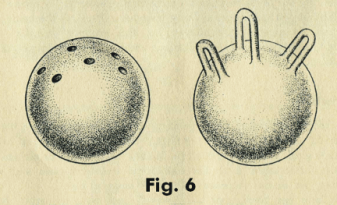
Let us take a spherical surface and cut 2p holes in it as shown in Fig. 6 (in Fig. 6, p = 3). Let us now divide these holes into p pairs and attach to each pair of holes a cylindrical tube ( a “handle”) as shown in the figure. We obtain a sphere with p “handles”. A sphere with p handles is topologically equivalent to a p-holed doughnut. See Fig. 7. A sphere with p handles is regarded as a normal surface or representative form for a surface of genus p. Any surface of genus p is topologically equivalent to it.

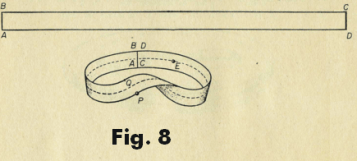
One-sided surfaces. All of the surfaces that we have considered thus far divide space into two domains, an interior and an exterior with the surface constituting the common boundary between the two domains. This fact is connected with another: Every one of the surfaces that we have considered have two sides, an interior and an exterior (one side can be painted in one color and the other in another). We shall now demonstrate some surfaces that have only one side. The first that we place on exhibit is the Mobius strip. A Mobius strip is constructed by taking a long rectangular band of paper and pasting the two ends together after giving it a half twist as shown in Fig. 8. One can easily confirm that there are not two sides on the strip (that could be painted in different colors): When we travel along the middle line starting our journey at, say, point E we arrive again at point E, but on the other side, and then continuing we arrive again at our start point. Incidently, the entire edge of a Mobius strip consists of a single closed curve. If we start at a point P on one edge of the band and travel along the edge we travel along both sides of the band before arriving at point P again.

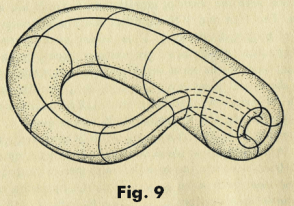
We now ask the following question. Are there any closed surfaces that are one-sided? In a sense they exist, in a kind of theoretical, mathematical sense. In a practical sense they don’t exist. The usual example of one is the “one-sided torus” or Klein bottle shown in Fig. 9. You couldn’t make one and must ignore the self-intersection to imagine one.

We can now present the fundamental theorem on the topology of surfaces as applied to two-sided surfaces:

Theorem. Every closed two-sided surface is homeomorphic to (topologically equivalent to) some normal surface of genus p, i.e., to a “sphere with p handles”. Any two closed two-sided surfaces are homeomorphic if and only if they are of one and the same genus p i.e. they are both homeomorphic to a sphere with p handles.

Normal forms for one-sided surfaces. There are also normal forms for one-sided surfaces analogous to the normal forms for closed two-sided surfaces but they are complicated to describe. Constructing them involves again starting with a sphere, cutting p circular holes in it, and then attaching to each of the holes a Mobius surface by pasting the edge of the surface to the edge of the corresponding hole. The problem is that it is a feat that is not physically possible and is thus difficult to visualize. Self-intersections arise immediately.

References

1. James & James. Mathematics Dictionary.

2. Mathematics, Its Content, Methods and Meaning. Vol. III

3. Richard Courant, Herbert Robbins. What is Mathematics?