Differentiation and integration. Monotonic functions. Jumps at discontinuities. Functions of bounded variation. Absolutely continuous functions. Theorems.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Indefinite integral. The indefinite integral of a function f(x) is any function F(x) whose derivative is f(x). It is given by

where c is an arbitrary constant. The integral

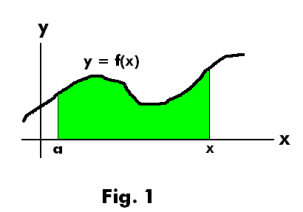
represents the area under the curve f(x) from an arbitrarily chosen point x = a to any point x as shown in Fig. 1.

Theorems on indefinite Riemann integrals

Theorem 1. If f(x) is bounded and Riemann integrable on [a, b], then

is continuous in [a, b].

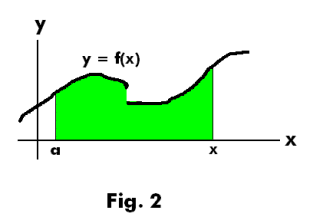
Theorem 2. A necessary and sufficient condition for a bounded function f(x) to be Riemann integrable in [a, b] is that the set of discontinuities of f(x) in [a, b] have measure zero.

From Theorems 1 and 2 we see that f(x) may be discontinuous but its integral F(x) will be continuous. Thus in Fig. 2 the function f(x) is discontinuous but its integral F(x) will be continuous.

Theorem 3. If f(x) is bounded and Riemann integrable on [a, b], then

at each point of continuity of f(x).

Fundamental theorem of calculus. Let f(x) be Riemann integrable on [a, b] and suppose that there exists a function F(x) continuous on [a, b] such that F'(x) = f(x). Then

or, equivalently,

***********************************************************************

Monotonic functions. A monotonic increasing function is a function that either increases or remains the same, never decreases i.e. a function f(x) such that f(x₂) ≥ f(x₁) for x₂ > x₁. A monotonic decreasing function is a function that either decreases or remains the same, never increases i.e. a function f(x) such that f(x₂) ≤ f(x₁) for x₂ > x₁. A monotonic function is a function that is either a monotonic increasing or monotonic decreasing.

Jump of a function. Figures 3a and 3b show “jumps” of a function at a discontinuity. The jump of a function f(x) at a discontinuity at x = a is defined as

(where x → a+ is read “x approaches a from the right” and x → a- is read “x approaches a from the left”). We note that a jump can be either positive or negative. The jump shown in Fig. 3a is a

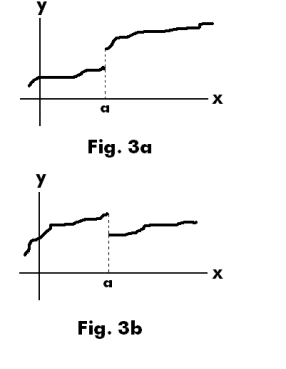
positive jump and the one shown in Fig. 3b is negative. If f(x) is monotonic increasing, the jump at any point is non-negative. If f(x) is monotonic decreasing, the jump at any point is non-positive. The function in Fig. 3a is monotonic (monotonic increasing) and the one in Fig. 3b is not.

Theorems on monotonic functions

Theorem 4. If f(x) is monotonic (increasing or decreasing) in the interval [a, b], then there can be at most a finite number of discontinuities with a jump whose magnitude is greater than some given ε > 0.

Theorem 5. If f(x) is monotonic (increasing or decreasing) in the interval [a, b], then the set of discontinuities of f(x) can at most be denumerable.

Functions of bounded variation

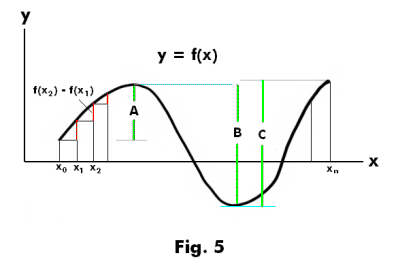
Def. Variation of a function in an interval. Let the interval [a, b] be divided into n parts by means of the points x₀, x₁, x₂, ... , x_n where

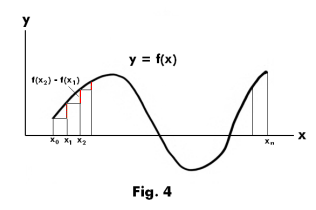
a = x₀ <x₁ < x₂ < ..... < x_n = b

as shown in Fig. 4. The variation of the function f(x) in the interval [a, b] is then defined as the least upper bound of the sum

for all possible modes of subdivision as n →∞. We denote the variation of f(x) in the interval [a, b] by .

Syn. Total variation

It can be seen that the variation of the function f(x) of Fig. 4 will be equal to the sum of the three line segments A, B and C shown in green in Fig. 5.

Def. Function of bounded variation in an interval. A function is said to be of bounded variation on an interval [a, b] if its variation on the interval is bounded. Such functions are called bounded variation functions or BV functions.

Intuitively, a function of bounded variation on an interval is one with finite arc length in the interval. If the arc is infinite in length the function is of unbounded variation. Let us consider some examples.

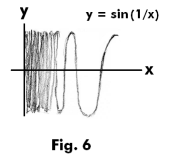
Example 1. The function

is of unbounded variation on the interval [0, 2/π]. See Fig. 6. As x → 0, this function oscillates an infinity of times between its limits of 1 and -1. The arc is then obviously of infinite length and the variation of the function in that interval is obviously unbounded.

Example 2. The function

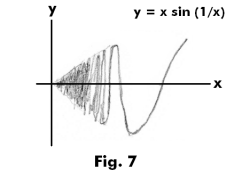
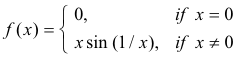
is of unbounded variation on the interval [0, 2/π]. See Fig. 7. As x → 0, this function also oscillates an infinity of times. The amplitude of the oscillations decrease, approaching zero as x → 0 . Thus it is not so obvious that this function is of unbounded variation on the interval.

Example 3. The function

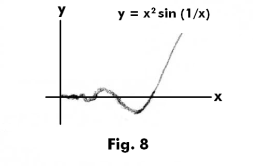
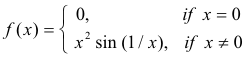
is of bounded variation on the interval [0, 2/π]. See Fig. 8. As x → 0, this function also oscillates an infinity of times. And the amplitude of the oscillations decrease, approaching zero as x → 0. In this case they are sufficiently small to make the variation bounded.

All three functions above are of bounded variation on any interval [a, b] if a > 0.

Theorems on functions of bounded variation

Theorem 6. A monotonic (increasing or decreasing) function on an interval [a, b] is of bounded variation on [a, b].

Theorem 7. If a function f(x) is of bounded variation on an interval [a, b], it is bounded on [a, b].

Theorem 8. If f(x) and g(x) are of bounded variation on an interval [a, b], so also are f(x) + g(x), f(x) - g(x), f(x)g(x), and f(x)/g(x) — where in the last case it is assumed that g(x) 0.

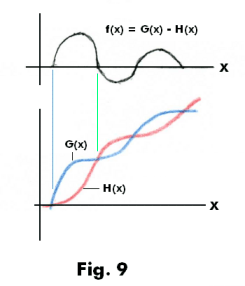
Jordan decomposition theorem. A function f(x) is of bounded variation if and only if it can be expressed as the difference G(x) - H(x) of two bounded monotonic increasing functions G(x) and H(x).

Example. See Fig. 9. The function f(x) is shown as the difference of the two monotonic increasing functions G(x) and H(x). Note that at points where G(x) and H(x) cross, f(x) is zero. Between its zeros f(x) is positive or negative depending on whether G(x) > H(x) or G(x) < H(x).

Theorem 9. If f(x) is of bounded variation in interval [a, b], it can have at most a denumerable set of discontinuities in [a, b] and at every point c in (a, b) the right and left hand limits and exist.

Theorem 10. If f(x) has a bounded derivative in [a, b], f(x) is of bounded variation in [a, b].

Theorem 11. If a function is monotonic, it has a derivative almost everywhere.

Theorem 12. If a function is bounded variation, it has a derivative almost everywhere.

Theorem 13. If

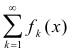
is a series of functions of bounded variation which converges to s(x) in [a, b], then

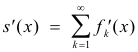
almost everywhere in [a, b].

We now introduce the very important concept of an absolutely continuous function.

Def. Absolutely continuous function. Let I be an interval in the real line R. Let P be any finite (or countable) set of non-overlapping sub-intervals

[a₁, b₁], [a₂, b₂], [a₃, b₃], ..... , [a_n, b_n]

within I. Let P_m be the measure of P (i.e. the sum of the lengths of the intervals). A function f:I R is absolutely continuous on I if for every positive number ε, there is a positive number δ such that, for any set of non-overlapping intervals P in I, if P_m < δ, then

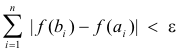
Observations. We note that the definition does not specify that the intervals [a_i, b_i] be either open or closed and so we assume they can be half open / closed. We also note that P can be any set of non-overlapping intervals in I and that includes all sets of contiguous non-overlapping intervals of the type described in the definition of the variation of a function. For such sets the expression

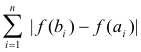
represents the variation of the function within that interval defined by the sum of the contiguous sub-intervals. Thus this definition tacitly implies conditions pertaining to the variation of the function. The importance of the property of absolute continuity for a function is that it is intricately connected to the question of the existence of the Lebesgue integral of a function as shown by the following theorem.

Theorem 14. A function f is absolutely continuous on a bounded closed interval [a, b] if and only if there exists a Lebesgue integrable function g on [a, b] such that

for all x on [a, b].

Theorem 15. The following conditions on a real-valued function f on a compact interval [a, b] are equivalent:

1) f is absolutely continuous

2) f has a derivative f ' almost everywhere, the derivative is Lebesgue integrable, and

for all x on [a, b].

3) there exists a Lebesgue integrable function g on [a, b] such that

for all x on [a, b].

Theorem 16. An absolutely continuous function is continuous and of bounded variation.

Note. A continuous function of bounded variation may or may not be absolutely continuous.

Theorem 17. If f(x) and g(x) are absolutely continuous on an interval [a, b], so also are f(x) + g(x), f(x) - g(x), f(x)g(x), and f(x)/g(x) — where in the last case it is assumed that g(x) ≠ 0.

Theorem 18. An absolutely continuous function has a derivative almost everywhere.

Theorem 19. If f(x) is absolutely continuous in an interval [a, b] and f '(x) = 0 almost everywhere in [a, b], then f(x) is a constant in [a, b].

Theorem 20. Let f(x) be absolutely continuous and strictly increasing in [a, b] [i.e. f(x_i) > f(x_i
-1) for x_i > x_{i -1} ]. Then if g(u) is absolutely continuous in [f(a), f(b)], g(f(x)) is absolutely continuous in [a, b].

References

James and James. Mathematics Dictionary

Spiegel. Real Variables (Schaum)

Mathematics, Its Content, Methods and Meaning.

Natanson. Theory of Functions of a Real Variable