Website owner:  James Miller

The Lebesgue integral. Theorems. Bounded, dominated, monotone convergence theorems.

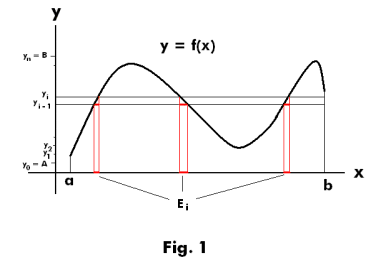
Lebesgue integral. Let f(x) be a bounded measurable function defined over a (Lebesgue) measurable set E of finite measure (for intuitive insight view f(x) as the function y = f(x) shown in Fig. 1 defined on the interval [a, b] --- where E corresponds to the interval [a, b]). Choose two real numbers A and B such that the range of y = f(x) lies between A and B [A and B represent lower and upper bounds of f(x)]. Divide the interval of the y axis from A to B up into n subintervals by choosing points y₀ = A, y₁, y₂, .... , y_n = B as shown in Fig. 1. Let

i.e. E_i is the subset of E consisting of the set of x ε E for which

See Fig. 1.

An approximation to the Lebesgue integral of the function f(x) is the Lebesgue integral sum

1)        S = y₁ · mE₁ + y₂ · mE₂ + .... + y_i · mE_i + ..... y_n · mE_n

where mE_i is the measure of point set E_i. The Lebesgue integral

is the limit of the Lebesgue integral sum S when max |y_{i -1} - y_i| 0 and n .

Note. In place of 1) the sum

2)        S = y₀ · mE₁ + y₁ · mE₂ + .... + y_{i -1} · mE_i + ..... y_{n -1} · mE_n

can also be used. Both give the same result.

Theorems on Lebesgue integrals of bounded functions

In the following we assume that all sets are measurable and of finite measure and that f(x) is bounded and measurable and thus Lebesgue integrable.

1. For any constant c

2. For any constant c

3. If E has measure zero, then

4. Mean-value theorem. If A f(x) B, then

5. If E = E₁ E₂ where E₁ and E₂ are disjoint, then

6. If E = E₁ E₂ where E₁, E₂, ..... are mutuallydisjoint, then

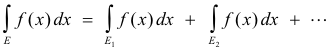
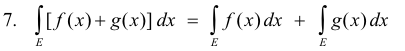
8. If f(x) and g(x) are bounded and measurable on E, then f(x)g(x) is Lebesgue integrable on E i.e.

9. If f(x) g(x) on E, or almost everywhere on E, then

10. If f(x) is bounded and measurable on E, then |f(x)| is Lebesgue integrable on E. Conversely, if |f(x)| is bounded and measurable on E, then f(x) is Lebesgue integrable on E.

11. If f(x) is bounded and measurable on E, then

12. If f(x) = g(x) almost everywhere on E, then

13. If f(x) 0 almost everywhere on E and

then f(x) = 0 almost everywhere on E.

The Lebesgue integral has one remarkable property that the Riemann integral does not have. It is the property given by the following theorem.

Bounded convergence theorem. Let {f_n(x)} be a sequence of measurable functions defined on an interval [a, b] that converges almost everywhere to f(x). If these functions are uniformly bounded i.e. there exists a constant K such that

            |f_n(x)| < K

for every n and every x in [a, b], then

Bounded convergence theorem for infinite series. Let u₁(x), u₂(x), .... be measurable on [a, b] and the partial sums

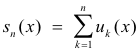
be uniformly bounded on E (i.e. there exists a constant K such that |s_n(x)| < K for every n and all x ε [a, b] ) and

Then

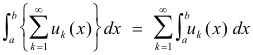
Relationship between Riemann and Lebesgue integrals. If f(x) is Riemann integrable in [a, b], then it is Lebesgue integrable in [a, b] and the two integrals are equal. The converse is, however, not true. If f(x) is Lebesgue integrable in [a, b], it need not be Riemann integrable in [a, b].

Theorem 1. A function is Riemann integrable in [a, b] if and only if the set of discontinuities of f(x) in [a, b] has measure zero i.e. if f(x) is continuous almost everywhere.

Theorem 2. If f(x) is continuous almost everywhere in [a, b], then it is Lebesgue integrable in [a, b]. 

*********************************************************************

Def. Lebesgue integral for unbounded functions. Let f(x) be an unbounded measurable function defined over a measurable set E of finite measure. Define as follows:

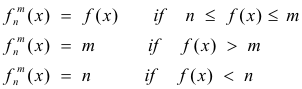
Then f(x) has the Lebesgue integral

provided this limit exists.                               

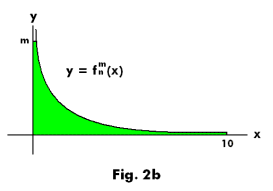
For intuitive insight see Fig. 2a and 2b for a function f(x) defined on the interval [0, 10].

If the set E does not have finite measure and

approaches a limit as the boundaries of an interval I all increase indefinitely, in any manner, then that limit is defined as

                                                                        James and James. Mathematics Dictionary

Theorems on Lebesgue integrals of bounded functions

In the following we assume that all sets and functions are measurable.

1. If f(x) 0, then

exists if and only if

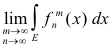
is uniformly bounded. 

2. If |f(x)| g(x) almost everywhere on E and g(x) is integrable on E, then f(x) is also integrable on E and

3. A function f(x) is integrable on E if and only if |f(x)| is integrable on E and in such case

Because of this we say that f(x) is integrable on E if and only if it is absolutely integrable on E.

4. If

exists, then f(x) is finite almost everywhere in E.

5. If E has measure zero, then

6. If

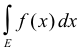
exists and if A is a measurable subset of E, then

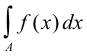
also exists. In such case we have

7. Let E = E₁ E₂ where E₁, E₂, ..... are mutually disjoint. Then if

exists 

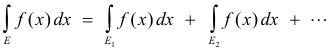
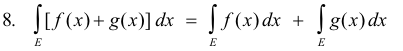
9. For any constant c

10. If f(x) is integrable on E and g(x) is bounded, then f(x)g(x) is integrable on E.

11. If f(x) = g(x) almost everywhere on E, then

12. If f(x) 0 almost everywhere on E and

then f(x) = 0 almost everywhere on E.

13. If f(x) is integrable on E, then given ε > 0 there exist a δ > 0 and a set A E such that if mA < δ

14. Let f(x) be integrable in E. If {E_k}is a sequence of sets contained in E such that = 0, then

Source: Spiegel. Real Variables (Schaum)

Dominated convergence theorem. Let {f_n(x)} be a sequence of measurable functions defined on an interval [a, b] that converges almost everywhere to f(x). Then if there exists a function M(x) integrable on E such that

            |f_n(x)| M(x)

for every n, then

Dominated convergence theorem for infinite series. Let u₁(x), u₂(x), .... be measurable on [a, b]. Let there exist an integrable function M(x) on [a, b] such that |s_n(x)| M(x) where s_n(x) is the partial sum

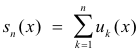
and let

Then

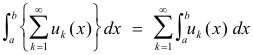
Theorem. If for the series

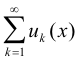
the condition

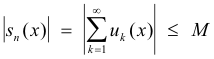
holds for some constant M and if v(x) is bounded and measurable on [a, b], then

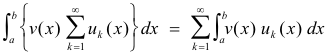
Fatou’s theorem. Let {f_n(x)} be a sequence of non-negative measurable functions defined on [a, b] and suppose that the sequence converges to f(x) almost everywhere. Then

Monotone convergence theorem. Let {f_n(x)} be a sequence of non-negative monotonic increasing functions defined on [a, b] and suppose that the sequence converges to f(x). Then

Theorem. Let u_k(x) 0, k = 1, 2, .... . Then

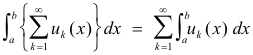
provided either side converges.

References

  James and James. Mathematics Dictionary

  Spiegel. Real Variables (Schaum)

  Mathematics, Its Content, Methods and Meaning.

  Natanson. Theory of Functions of a Real Variable