Website owner: James Miller
Differential equations. Definitions. Order, degree. General, particular and singular solutions.
Definitions
Def. Differential equation. A differential equation is an equation containing derivatives of a dependent variable with respect to one or more or independent variables. The following are typical examples:
![]()
![]()
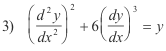
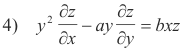
When only the first derivative is involved the equation is frequently written in terms of differentials. For example 2) above could be written
![]()
Def. Ordinary differential equation. A differential equation containing a single independent variable. The derivatives occurring in the equation are ordinary derivatives.
Def. Partial differential equation. A differential equation containing two or more independent variables. The derivatives occurring in the equation are partial derivatives.
Def. Order of a differential equation. The order of the highest ordered derivative occurring in the equation. Equations 2) and 4) above are of the first order and equations 1) and 3) are of the second order.
Def. Degree of a differential equation. In general, the degree of the highest ordered derivative occurring in the equation. However, not every differential equation has a degree. If the derivatives occur within radicals or fractions the equation may not have a degree. If the equation can be rationalized and cleared of fractions with regard to all derivatives present, then its degree is the degree of the highest ordered derivative occurring in the equation.
Example. Equations 1), 2) and 4) above are of the first degree and equation 3) is of the second degree. The differential equation (y'')2/3 = 2 + 3y' can be rationalized by cubing both sides to obtain (y'')2 = (2 + 3y' )3. Thus it is of degree two.
Def. Linear differential equation. A linear differential equation is an equation of the form
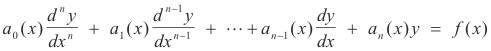
where the ai(x) are functions of x only. It is an equation in which each term is of first degree in the dependent variable and its derivatives.
Solutions of differential equations. A solution of a differential equation is any relation, free of derivatives, between the variables involved that reduces the differential equation to an identity. The solution may take the form of the dependent variable being expressed explicitly as a function of the independent variable (or variables) as in y = f(x) or implicitly as in a relation of the type f(x, y) = 0.
Def. Essential constants. A set of constants are called essential if they cannot be replaced by a smaller number of constants.
Solution contains n essential arbitrary constants. An example of a very simple differential equation is one of the form
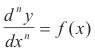
Solving such an equation involves n repeated integrations where each integration gives rise to an arbitrary constant. Thus the solution contains n essential arbitrary constants. For example, in the equation
![]()
we have, after integrating twice,
y = x3 + C1x + C2
This result is called the general solution of the differential equation. Any solution that can be obtained from it by giving particular values to C1 and C2 is called a particular solution.
The general solution of a differential equation is also called the primitive.
Theorem. The general solution or primitive of a differential equation of order n always contains exactly n essential arbitrary constants.
Singular solutions. In addition to the general solution a differential equation may also have a singular solution. A singular solution is a solution not obtainable by assigning particular values to the arbitrary constants of the general solution. It is the equation of an envelope of the family of curves represented by the general solution. This envelope satisfies the differential equation because at every one of its points its slope and the coordinates of the point are the same as those of some member of the family of curves representing the general solution.
James/James. Mathematics Dictionary
Existence of solutions. Not every differential equation has a solution. For example, there cannot be any real function that satisfies the differential equation
(y')2 + 1 = 0
Why? Because for any real function, the left-hand side of the equation will be greater than, or equal to, one and thus cannot be zero. In fact, only relatively few differential equations have solutions. Of those that do, only a few can be solved in closed analytic form. Only a few can be solved in terms of the elementary functions (i.e. the rational algebraic, trigonometric, exponential and logarithmic functions familiar from elementary calculus). Some others can be solved in terms of higher transcendental functions. For the rest one must use numerical approximation methods such as power series representation.
Most differential equations arise from problems in physics, engineering and science. These equations often have certain conditions called boundary or initial conditions associated with them that they must satisfy. We then must ask not only if a solution exists for the equation but, also, if one exists that will also satisfy the stated initial conditions. For example, suppose we wish to solve the differential equation
xy' - 2y = 0
subject to the initial condition x = 0, y = 1. The general solution of the equation is
5) y = Ax2
but examination of 5) shows that there is no value of A that will satisfy the initial conditions.
Methods of solution. There is no general procedure for solving a differential equation. Only a few simple equations can be solved by integrating directly. Most equations are solved by techniques devised for a particular type of equation. Each of the various types has its own method of solution. Generally, to solve an equation one must be able to recognize the type and recall the proper method for solving it.
References
1. Ross R. Middlemiss. Differential and Integral Calculus. Chap. XXIX
2. James/James. Mathematics Dictionary.
3. Murray R. Spiegel. Applied Differential Equations.
4. James B. Scarborough. Differential Equations and Applications.
5. Frank Ayres. Differential Equations (Schaum).
6. Eshbach. Handbook of Engineering Fundamentals.
7. Earl Rainville. Elementary Differential Equations.
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life