Website owner: James Miller
Ratio, proportion, variation. Arithmetic, geometric, harmonic progression. Geometric series. Permutations. Combinations. Binomial formula. Pascal’s Triangle. Inequalities.
Ratio, proportion, variation.
Def. Ratio. The ratio a:b of two numbers a and b is the fraction a/b e.g. the ratio 2:3 is the fraction 2/3.
Def. Proportion. A statement of equality of two ratios i.e. an equation whose members are ratios as in
![]()
Here a and d are called the extremes and b and c are called the means.
Laws of proportion. If
![]()
then the following hold:
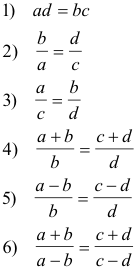
Def. Direct variation. A variable y is said to vary directly as another variable x if y is equal to some constant c times x i.e. y = cx.
Def. Inverse variation. A variable y is said to vary inversely as another variable x if y varies directly as the reciprocal of x i.e. y = c/x.
Def. Joint variation. A variable z is said to vary jointly as x and y if z varies directly as the product xy i.e. zcxy = cxy.
Progressions
Def. Sequence. A sequence is a set of numbers or quantities arranged in a definite order. The numbers of a sequence are called terms. Sequences may be finite or infinite.
Def. Arithmetic Progression. A sequence of numbers, each of which is equal to the preceding term and a constant. If a denotes the first term and d the constant, any arithmetic progression is represented by
a, a + d, a + 2d, a + 3d, a + 4d, .... .
The number d is called the common difference and may be any number, positive or negative.
Syn. Arithmetic sequence.
Examples.
1) 2, 5, 8, 11, 14, ...
2) 8, 4, 0, -4, -8 -12, ...
3) ½, 3, 5½, 8, 10½, ...
Formulas for n-th term and sum of n terms of an arithmetic progression. If a is the first term, d the common difference, n the number of terms, l the n-th term (last term), and S the sum of n terms, then the formulas for the n-th term and sum of n terms are given by
n-th term:
l = a + (n - 1)d
Sum of n terms:
![]()
Def. Geometric progression. A sequence of numbers each of which, after the first, is obtained by multiplying the preceding number by a constant called the common ratio. If a denotes the first term and r the common ratio, the progression is represented by
a, ar, ar2, ar3, ar4, ...
Example. 3, 6, 12, 24, 48, ... is a geometric progression whose common ratio is 2.
Formula for n-th term and sum of n terms of an geometric progression. If a is the first term, r the common ratio, n the number of terms, l the n-th term (last term), and S the sum of n terms, then the formulas for the n-th term and sum of n terms are given by
n-th term:
l = arn-1
Sum of n terms:
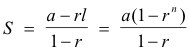
If r is numerically less than 1, S approaches the limit S∞ as n increases without limit
![]()
Def. Geometric series. The indicated sum of the first n terms of a geometric progression
Sn = r + ar + ar2 + ar3 + .... + ar n-1
This sum is given by
![]()
Def. Harmonic Progression. A sequence of numbers whose reciprocals form an arithmetic progression.
Example. The sequence
![]()
is a harmonic progression since 2, 4, 6, 8, 10, ... is an arithmetic progression.
Permutations and combinations
Fundamental Principle. If one thing can be done in m different ways, and after it is done a second thing can be done in n different ways, then the two things can be done in succession in mn different ways.
Example 1. Q. In walking from point A to point B one can take any one of three roads. In going from point B to point C he has a choice of four roads. By how many different routes can he walk from A to C? A. 3×4 = 12 different routes.
Example 2. Q. At a restaurant one is offered a choice of four meat courses and five deserts. In how many ways can he select a meal consisting of a meat course and a desert? A. 4×5 = 20 ways.
Example 3. Q. In how many ways can one select a meal from a choice of three soups, four meats, and three deserts? A. 3×4×3 =36 ways.
Def. Permutation. An ordered arrangement or sequence of all or part of a set of things. If we are given a set of n different objects and arrange r of them in a definite order, such an ordered arrangement is called a permutation of the n objects r at a time. For example, the permutations of the three letters a, b, c taken all at a time are abc, acb, bca, bac, cba, cab. Each of these represents a separate permutation of the letters a, b, c. The permutations of the three letters a, b, c taken two at a time are ab, ac, ba, bc, ca, cb.
The number of permutations that can be formed in a particular situation is found by using the Fundamental Principle stated above.
Example 1. How many permutations of four letters can be formed from the letters a, b, c, d, e, f, g?
Solution. Seven letters can be put in the first position, then six letters can be put in the second position, then five letters can be put in the third position, then four letters can be put in the fourth position. Thus the answer is 7∙6∙5∙4 = 840.
Example 2. How many integers of four figures can be formed from the nine digits 1, 2, 3, 4, 5, 6, 7, 8, 9 if none is used twice?
Solution. Nine numbers can be put in the first position, then eight numbers can be put in the second position, then seven numbers can be put in the third position, then six numbers can be put in the fourth position. Thus the answer is 9∙8∙7∙6 = 3024
The number of permutations of n things taken r at a time is denoted by nPr.
Theorem 1. The number of permutations of n different things taken r at a time is
nPr = n(n-1)(n-2) ... (n - r + 1)
Note that the product n(n-1)(n-2) ... (n - r + 1) in the right member contains exactly r factors.
Factorial notion. If n is a positive integer, the symbol n!, which is read “n factorial” or “factorial n,” denotes the product of the first n integers:
n! = 1∙2∙3∙ ... ∙n
This definition of factorial leaves the case when n is zero meaningless. In order to make certain formulas valid in all cases, factorial zero is arbitrarily defined to be 1.
Example. 5! = 1∙2∙3∙4∙5 = 120
Theorem 2. The number of permutations of n different things taken all at a time is
nPn = n(n-1)(n-2) ... 1 = n!
Circular permutations.
Theorem 3. The number of ways of arranging n different objects around a circle is (n - 1)! ways.
Number of permutations of n things with some things alike. The letters of the word formula are all different and thus can be arranged in 7! distinct ways. However, in the word between there are three letters that are alike and thus cannot be distinguished from each other in any arrangement that we make. It is obvious that the number of distinct permutations of the letters in the word between will be less than 7!. How many distinct permutations can be made from the word between? Using the following theorem we find it is 7! / 3!.
Theorem 4. Given n objects, of which k1 are alike, k2 others are alike, k3 others are alike, etc.; The number of different permutations that can be made of the n objects taking them all at a time is
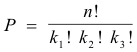
Def. Combination. A combination of a set of objects is any subset without regard to order. If we are given a set of n objects, any selection or set of r of the objects, considered without regard to their arrangement, is a combination of the n objects r at a time.
Example. The combinations of the letters a, b, c taken two at a time are ab, ac, bc. We note that ab and ba are two permutations but one combination.
The number of combinations of n things taken r at a time is denoted by nCr.
Theorem 5. The number of combinations of n things taken r at a time is
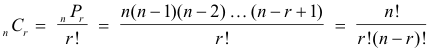
Note that nCr = nCn-r .
A systematic procedure for finding and listing all combinations of n objects taken r at a time
Theorem 6. The total number of combinations of n things taking them any number at a time (i.e. 1, 2, 3, ... , n at a time) is given by
nC1 + nC2 + nC3 + ..... + nCn = 2n - 1
Binomial Formula. If n is a positive integer
![]()
which can also be written as
2) (x + y)n = xn + nC1xn-1y + nC2xn-2y2 + nC3xn-3y3 + ..... + yn
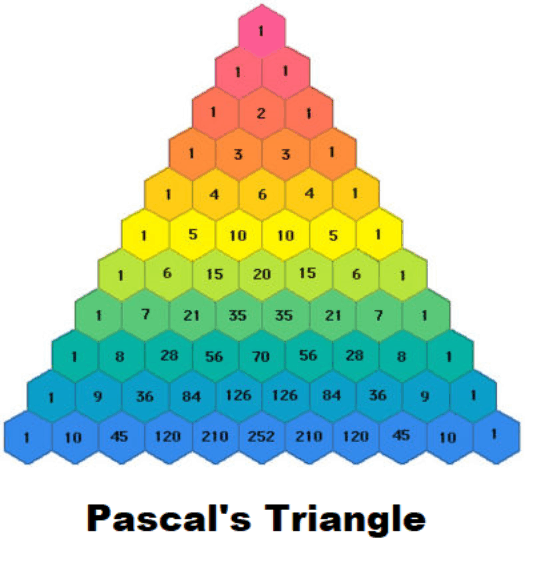
Pascal’s Triangle. To the right is pictured the first 11 rows of Pascal’s Triangle. The triangle is formed as follows: The first and last numbers of each row is a 1. Each number in the interior of the triangle is the sum of the two numbers to the right and left above it. We thus work down from the top computing the numbers of each row from the numbers above it.
Connection between Pascal’s triangle and Binomial Formula. The coefficients on the right side of 2) are precisely the numbers on row n of Pascal’s Triangle (the first row is 1 1, the second row is 1 2 1, etc. — neglecting the 1 at the top vertex)
The binomial formula also holds for negative and fractional values of n. However, when n is a negative or fractional number the expansion does not terminate. In this case it is an infinite series called the binomial series. Such an expansion converges and its sum is (x + y)n if |y| < |x|, or if x = y ≠0 and n > -1, or if x = -y ≠0 and n > 0.
Inequalities
Def. Inequality. A statement that one quantity is less than (or greater than) another.
a > b means a is greater than b
a < b means a is less than b
a
![]() b means a is greater than or equal to b
b means a is greater than or equal to b
a
![]() b means a is less than or equal to b
b means a is less than or equal to b
Def. Absolute inequality. An inequality which is true for all values of the variables (or contains no variables).
Examples. x + 2 > x, 5 > 3, (a + b)2 > -1
Def. Conditional inequality. An inequality that holds only for particular values of the variables.
Example. x +3 > 5 because it holds only for x > 2
Sense of an inequality. The direction (greater than or less than) in which the inequality sign points is the sense of an inequality. This is used in such phrases as same sense and opposite sense. The inequalities a < b and c < d, or b > a and d > c, are said to have the same sense; the inequalities a < b and d > c are said to have opposite senses.
Laws of inequalities
1) The sense of an inequality is not changed if the same number is added to (or subtracted from) both members;
if a > b, then a + c > b + c and a - c > b - c
This means that any number can be transposed from one side of an inequality to the other if its sign is changed; and that any term common to both members can be cancelled.
2) The sense of an inequality is not changed if both members are multiplied (or divided) by the same positive number;
![]()
3) The sense of an inequality is reversed if both members are multiplied (or divided) by the same negative number.
![]()
4) If a > b and a, b, n are positive, then an > bn but a-n < b-n
5) If a > b and c > d, then (a + c) > (b + d)
6) If a > b > 0 and c > d > 0, then ac > bd
References
Hawks, Luby, Touton. First-Year Algebra
Hawks, Luby, Touton. Second-Year Algebra
Murray R. Spiegel. College Algebra (Schaum)
Raymond W. Brink. A First Year of College Mathematics
Frank Ayres. First Year College Mathematics (Schaum)
James / James. Mathematics Dictionary
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life