Exponents. Algebraic expressions, terms and operations. Removal of parenthesis. Multiplication and division of polynomials.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Symbols used to denote multiplication. In algebra, the operation of multiplication can be indicated in any of several ways. It can be indicated by the usual times sign as in 8×a, by a dot as in 8∙a, by parentheses as in (8)(a), or by simply writing the numbers close together as in 8a.

Example. a×b can also be written as a∙b, (a)(b) or ab.

Symbols used to denote division. Division of a number a by a number b is denoted by a÷b, a/b or .

Exponents and powers. When a number a is multiplied by itself n times, the product a∙a∙a∙ ... ∙a (n times) is written as aⁿ and is referred to as ‘the n-th power of a’ or ‘a to the n-th power’. In aⁿ, the number a is called the base and n is the exponent.

Examples.

2³= 2×2×2

a⁴ = a∙a∙a∙a

Zero exponent. We define the value of a⁰ to be:

a⁰ = 1 providing a≠0

Examples. 3⁰ = 1; (-5)⁰ =1; x⁰ = 1;

Negative integral exponents. If n is a positive integer, we define a^-n as:

Examples.

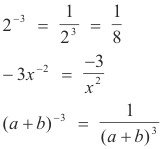
Roots. If n is a positive integer and aⁿ = b, then a is said to be the n-th root of b. Let us now note that in the extended number system that we have created that includes negative numbers (i.e. the real number system) not only does 2² = 4 but also (-2)² = 4. Also, 2⁴ = 16 and (-2)⁴ = 16. In general, if b is positive and n is even there are two roots, a positive root and a negative root. The positive root is called the principal root. If b is positive and n is odd there is a single positive root. For the case when b is negative and n is odd there is a single root and it is negative. When b is negative and n is even there are no roots. In summary, for the n-th roots of b:

b positive, n even: Two roots, a positive and negative root

b positive, n odd. One positive root

b negative, n even. No root

b negative, n odd. One negative root

Fractional exponents. If the exponent on a symbol x is a fraction p/q, then x^p/q is defined as (x^1/q)^p, where x^1/q is the positive q-th root of x if x is positive and the (negative) q-th root if x is negative and q is odd.

Example.

Laws of exponents. If p and q are real numbers, the following laws hold:

1. a^p∙a^q = a^p+q

Examples. 3² ∙3⁴ = 3⁶, 2^-3 ∙2⁵ = 2², 2^1/3 ∙2^1/6 = 2^1/2

2. (a^p)^q = a^pq

Examples. (2²)³ = 2⁶, (4^1/3)^-3= 4^-1 = 1/4, (a^2/3)^3/4 = a^1/2

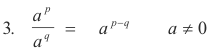
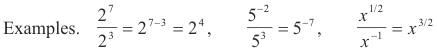
4. (ab)^p = a^pb^p

Examples. (3 ∙5)⁴ =3⁴ ∙5⁴, (3x)³ = 3³x³, (4a)^½ = 4^1/2a^1/2 = 2a^1/2

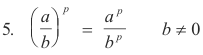
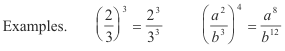
Algebraic operations and expressions

Def. Algebraic Operation. The operations of addition, subtraction, multiplication, division, extraction of roots, and raising to integral and fractional powers.

Def. Algebraic expression. An expression using only letters representing numbers, numbers, and algebraic operations.

Examples. The following are examples of algebraic expressions:

2x² -1

8m - 3

5x⁴ - 2(x² + 4x - 2)

2a - 5b + 1

5x - (2x²+1)/(4x -1)

3x² +

Def. Term. In an algebraic expression that consists of a sum of several quantities, each of the quantities is called a term of the expression.

Example. The algebraic expression

5x³ + 2x² - 6x + 1

has the four terms 5x³, 2x², - 6x and 1.

Def. Coefficient. The numerical part of a term, usually written before the literal part.

Example. The coefficient of the term 5x³ is 5; the coefficient of -3x²y⁴is -3.

Def. Like terms. Like terms are terms which have identical literal parts i.e. they are terms that differ only in their coefficients.

Examples. 5x² and -8x² are like terms; 5xy and -2xy are like terms; 5x²y³ and -3x²y³ are like terms; 5x²y³ and -3x²y⁵ are not like terms.

Def. Monomial, binomial, trinomial, multinomial. A monomial is an algebraic expression consisting of only one term, a binomial is an algebraic expression consisting of two terms and a trinomial is an algebraic expression consisting of three terms. A multinomial is an algebraic expression consisting of more than one term.

Example. 5x²y³ is a monomial, 4xy + y² is a binomial, etc,

Def. Integral expression. An algebraic expression in which no variables appear in any denominator when the expression is written in a form having only positive exponents.

Example. The expression x² + 3x^5/3 + y^1/2 is an integral expression. The expression

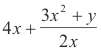
is not.

Def. Radical. (1) The indicated root of a quantity, as and (2) The sign indicating a root to be taken, a radical sign (the sign √ placed before a quantity to indicate that its root is to be taken).

Def. Rational expression. An expression which involves no variable in an irreducible radical or under a fractional exponent. An irreducible radical is one that cannot be written in an equivalent rational form. The radicals and are irreducible, whereas and are reducible since they are equivalent to 2 and x.

Example. The expressions 3x² + 2y³ - 1 and 5x² + 2/x are rational expressions. The expressions x^3/2 + 5 and (x + 2)^½ are not.

Def. Rational integral term. A rational integral term in the variables x, y, z, ... is a term of the form ax^py^qz^r... where the variables p, q, r, ... are either positive integers or zero and the coefficient a is a constant.

Examples. 4x³yz², 3x², 5 are all rational integral terms.

Def. Degree of a rational integral term. The sum of the exponents of the variables i.e. the degree of ax^py^qz^r is p + q + r .

Example. The degree of 6x²y⁵ is 7.

Def. Polynomial. A polynomial in one variable (usually simply called a polynomial) of degree n is a rational integral algebraic expression of the form

a₀xⁿ + a₁x^n-1 + .... a_n-1x + a_n

where n is a nonnegative integer.

A polynomial in several variables is a rational integral expression consisting of a sum of terms, each term being the product of a constant and various nonnegative integral powers of the variables.

Example. 3x³y - 2xy³ + 5y² - 3z⁴ + 6 is a polynomial in three variables.

Def. Degree of a polynomial. The degree of the term of highest degree.

Examples. The degree of

3x² + 2x⁴y - 2xy³ + 5y² - 3z⁴ + 6

is the degree of the term 2x⁴y, which is 5.

The degree of

3x⁴ + 2x² - x + 1

is 4.

Parenthesis, brackets, braces, and other grouping symbols

Rules on the removal of parenthesis, brackets, braces, and other grouping symbols. Parentheses, brackets, braces, etc. are employed in grouping terms. The following rules apply.

1. If a + sign precedes a symbol of grouping, this symbol of grouping can be removed without affecting the terms contained within.

Example. (2x - y²) + (5x² + 2) = 2x - y² + 5x² + 2

2. If a - sign precedes a symbol of grouping, this symbol of grouping can be removed providing the sign of each of the terms contained within is changed.

Example. (2x - 3y) - (y² + 1) = 2x - 3y - y² - 1

3. If one set of grouping symbols is contained within another, the innermost must be removed first.

Example. 3x - {4x² - (2xy - 3y)} = 3x - {4x² + 2xy + 3y} = 3x - 4x² - 2xy - 3y

Multiplication and division of expressions

Multiplication of monomials. Multiplication of monomials involves applying the laws of exponents.

Example. (5xy²)(2x³y⁴) = 10x⁴y⁶

Multiplication of multinomials. Multiplication of multinomials involves applying the commutative and distributive laws for multiplication i.e. the laws ab = ba and a(b + c) = (b + c)a = ab + ac. As the following example shows, the product of two multinomials is obtained by multiplying each of the terms of one multinomial by each of the terms of the other multinomial.

Example. (a + b + c)(d + e + f) = a(d + e + f) + b(d + e + f) + c(d + e + f)

= ad + ae + af

+ bd + be + bf

+ cd + ce + cf

Division of polynomials. To divide one polynomial by another:

1. Arrange the terms of the two polynomials in descending powers of the variable.

2. Divide the first term of the dividend by the first term of the divisor to obtain the first term of the quotient.

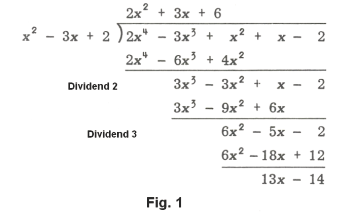
3. Multiply the entire divisor by this first term of the quotient, placing the product under like terms of the dividend. Now subtract from the dividend to obtain the first partial remainder.

4. Use this remainder as a new dividend and divide its first term by the first term of the divisor, to obtain the second term of the quotient.

5. Continue this process until a remainder is obtained which is either zero or of lower degree than the divisor.

The process is similar to that used in long division in arithmetic.

Problem. Divide x² + 2x⁴ - 3x³ + x - 2 by x² - 3x + 2.

Solution. See Fig. 1. The solution is

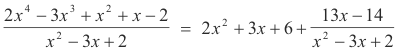
References

Hawks, Luby, Touton. First-Year Algebra

Murray R. Spiegel. College Algebra

Raymond W. Brink. A First Year of College Mathematics