Frequently used formulas

1. Euler’s formula. The formula e^{i θ} = cos θ + i sin θ . Interesting special cases are those in which θ = π and 2π for which e^πi = -1 and e^2πi = 1, respectively.

2. Expressions for a complex number in polar coordinates.

         z = x + iy = r(cos θ + i sin θ)

         z = x + iy = re^{i θ}

3.     For complex numbers   z₁ = r₁ (cos θ₁ + i sin θ₁) and z₂ = r₂ (cos θ₂ + i sin θ₂):

          z₁z₂ = r₁r₂ [cos (θ₁ + θ₂) + i sin (θ₁ + θ₂)]

          z₁z₂ ... z_n = r₁r₂ ... z_n [cos (θ₁ + θ₂ + ... + θ_n) + i sin (θ₁ + θ₂ + ... + θ_n)]

          z₁/z₂ = ( r₁/r₂) [cos (θ₁ - θ₂) + i sin (θ₁ - θ₂)]

          zⁿ = [ r(cos θ + i sin θ)]ⁿ = rⁿ (cos nθ + i sin n)

         ln z = ln r + iθ

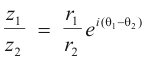
          e^z = e ^{x + iy} = e^x (cos y + i sin y)

          a^z = e ^{z ln a}    where a is either real or complex

         e^πi = -1

         e^2πi = 1

4. For a complex variable z = x + iy

         e^iz = cos z + i sin z

         e ^-iz = cos z - i sin z

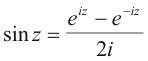
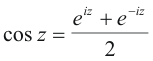
5. For a real variable x

          e^ix = cos x + i sin x

          e ^-ix = cos x - i sin x

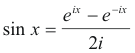
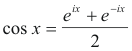
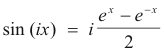
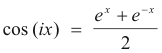
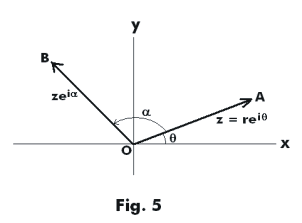
Geometric meaning of multiplication of a vector z by e^iα . Let z = re^iθ be the vector OA in Fig. 5. Then the product

            ze^iα = re^iθe^iα = re^i(θ+α)

is the vector OB shown in the figure. Multiplication of a vector z by e^iα amounts to rotating z counterclockwise by an angle α. We can consider e^iα as an operator which acts on z to produce this rotation.