Multiple-valued functions, branch points, branch lines, Riemann surfaces

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Multiple-valued functions, branch points, branch lines

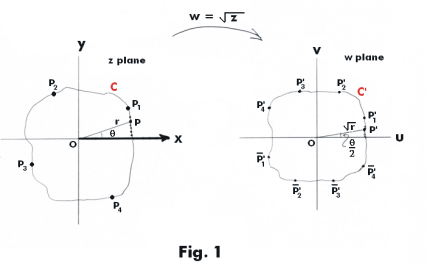
Example 1. Suppose we are given the function w = z^1/2 and ask ourselves how this function will map points taken along curve C which encircles the origin as shown in Fig. 1. We pick points along the curve and let z make a complete circuit (counterclockwise) around the origin. For insight into what is happening we express z as z = re^iθ. The image of z in the w plane is then given by w = e^iθ/2. Thus each point P(r, θ) is mapped into its image P'( , θ/2). Point P₁(r₁, θ₁) is imaged into P₁'( , θ₁/2). P₂, P₃ and P₄ are imaged into points P₂', P₃' and P₄' as shown in the figure. Each point P is mapped into its image P' in the w plane where P' has half the amplitude of P. We make a complete circuit around curve C and arrive back at point P₁ again. The amplitude of P₁ is now θ = θ₁ + 2π. Point P₁(r₁, θ₁ + 2π) is imaged into point (r₁, θ₁/2 + π) shown in the figure in the third quadrant of the w plane, where we are denoting the images of points from the second circuit around C with an over-bar. As we continue points P₂, P₃ and P₄ map into points and as shown in the figure. Finally we arrive at point P₁ for the third time and the amplitude is now θ = θ₁ + 4π. This time point P₁ maps into the same point that it did on the first trip through, point P₁', and the process starts over again.

We can describe the above process by saying that if 0 θ < 2π we are on one branch of multiple-valued function z^1/2, while if 2π θ < 4π we are on the other branch of the function.

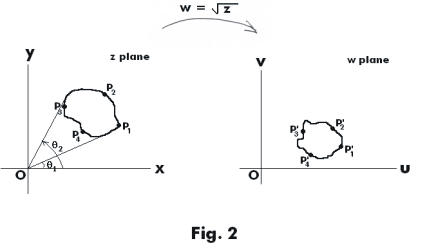
The above phenomenon in which a point P on C maps into two points on C' occurs because curve C encircles the origin. If C did not encircle the origin it wouldn’t happen. A point on C would then map into a single point on C'. Let us consider this case. See Fig. 2. In Fig. 2 we see that the amplitude of z varies between θ₁ and θ₂. The amplitude of w will then vary between θ₁/2 and θ₂ /2. Point P₁ will be mapped only into point P₁', P₂ will be mapped only into point P₂', etc. The mapping is different and one-to-one.

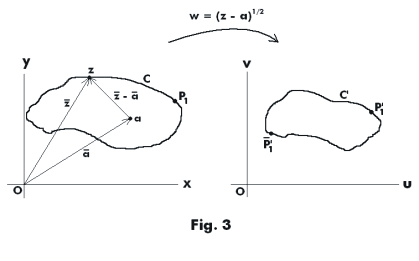
Example 2. Let us now consider how the function w = (z - a)^1/2 maps a curve C that encircles point a. See Fig. 3. is the position vector to point z on the curve. is the position vector to point a. As point z moves counterclockwise around curve C the vector , extending from point a to z, winds around point a. On the first trip around the curve, point P₁ is mapped into point P₁'. Assume the amplitude of the vector is θ₁ at P₁. Note that arg w = arg (z - a) so the amplitude of w will be θ₁ /2. When z has made a complete circuit and arrives at P₁ the second time the amplitude of will be θ₁ + 2π and the amplitude of w will be θ₁/2 + π. P₁ will map into . When z proceeds on around the circuit again and arrives at P₁ for the third time, the amplitude of will be 4π, the amplitude of w will be θ₁ /2 + 2π, and P₁ will map into P₁' again.

Branch point. If different values of a function f(z) are obtained by successively encircling some point z₀ in the complex plane, as occurred in examples 1 and 2 above, then the point z₀ is called a branch point. In Example 1 the origin O is a branch point and in Example 2, the point a is a branch point.

A branch point represents a singularity of a multi-valued function, however, it has a different character from the points ordinarily called singular points.

Example 3. f(z) = (z - 2)^1/3 has a branch point at z = 2.

Example 4. f(z) = ln (z² + z - 6) has branch points where z² + z - 6 = 0, i.e. at z = 2 and z = -3.

Branch line. A branch line is a line extending out from a branch point defining a boundary between branches. When a variable z crosses a branch line the function f(z) switches from one branch to another. The heavy line OX in Fig. 1 extending from the branch point O to infinity is a branch line.

Riemann surface. Let z₀ be any complex number. How many complex numbers w will satisfy the equation w⁵ = z₀? Answer: There are five different complex numbers that will satisfy this equation. If we pick any number z₀ in the complex plane there are five different fifth roots of z₀. Thus we say that the function w = z^1/5 is a 5-value function. Five different numbers satisfy it. The function w = z^1/5 associates with each point z in the complex plane five different numbers. Let us designate these five numbers as s₁, s₂, ... , s₅. We can now conceive of five “sheets of values” overlaying the z plane, one stacked on top of another, going from Sheet 1 up to Sheet 5. The first sheet consists of the s₁ numbers for all (x, y) number pairs in the plane i.e. all points of the plane. The second sheet consists of the s₂ numbers for all (x, y) number pairs in the plane. Etc. for all five sheets. A function w = z^1/2 has two sheets associated with it. A function w = z^1/8 has eight sheets associated with it. The five sheets associated with the 5-value function w = z^1/5 represent the five branches of the function. They represent the five sheets of a 5-sheet Riemann surface. The Riemann surface consists of a collection of five sheets where each sheet represents a single-valued function. The sheets in a Riemann surface are conceived of as connected to one another. To understand how they are connected consider the case of a 2-sheet Riemann surface where the branch point is the origin O as in Example 1 above. Imagine the two sheets, Sheet 1 and Sheet 2, overlaying the z plane. Now cut both sheets along OX and imagine that the lower edge of the bottom sheet is joined to the upper edge of the top sheet. Then starting in the bottom sheet and making one complete circuit around the branch point we arrive in the top sheet when we cross the branch line (or branch cut) OX. We must now imagine the other cut edges joined together so that by continuing the circuit we go from the top sheet back to the bottom sheet.