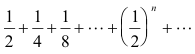
Website owner: James Miller
SERIES, ALTERNATING SERIES, POWER SERIES, CONVERGENCE
Def. Series. The indicated sum of a finite or infinite sequence of terms. It is a finite or an infinite series according as the number of terms is finite or infinite. An infinite series can be written in the form
a1 + a2 + a3 + ... + an + ...
or Σ an, where an is the general term or the n-th term. Infinite series is usually shortened to series, as in convergent series, Taylor’s series, etc. A series is a positive series if its terms are all positive real numbers and a negative series if they are all negative real numbers.
James and James. Mathematics Dictionary.
Def. Sum of an infinite series. An infinite series of numbers has no sum within the ordinary meaning of the word since no matter how many of the terms one might add, there would always be an unlimited number of them left over. We must therefore define a meaning for the term sum as applied to infinite series.
Consider a series
u1 + u2 + u3 + ... + un + ...
and the sequence of partial sums S1, S2, S3, ... where
S1 = u1
S2 = u1 + u2
S3 = u1 + u2 + u3
...............................
Sn = u1 + u2 + u3 + .... + un
If Sn, regarded as a function of n, approaches a limit S as n → ∞, this limit is called the sum of the infinite series and the series is said to be convergent. If Sn does not approach a limit as n → ∞, the series is said to be divergent.
Example. The sum of the series
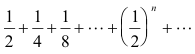
is 1, because that is the limit approached by the sum of the first n of these terms, namely 1 - 1/2n, as n becomes infinite. The sum of the series is precisely 1, even though the actual arithmetic sum of a finite number of terms of the series is always less than 1. The series 1 + (-1) + 1 + (-1) + 1 + ... does not have a sum, since the sum of the first n terms is + 1 if n is odd and 0 if n is even and therefore the sum of the first n terms does not have a limit as n increases.
A series can converge in only one way: lim Sn as n → ∞ must exist (and be finite). But a series can diverge in two ways:
![]()
![]()
Example. The limit of the series
1 + (-1) + 1 + (-1) + 1 + ...
just simply fails to exist.
Middlemiss. Differential and Integral Calculus.
James and James. Mathematics Dictionary.
Theorem. Multiplication of each term of a series by a constant different from zero does not affect the convergence or divergence. Removal (or addition) of a finite number of terms from (or to) a series does not affect the convergence or divergence.
Def. Mixed-term series. A series that contains an unlimited number of both positive and negative terms.
Def. Alternating series. A series whose terms are alternately positive and negative, as
![]()
An alternating series converges if each term is numerically equal to or less than the preceding and if the n-th term approaches zero as n increases without limit. This is a sufficient, but not a necessary set of conditions — the term-by-term sum of any two convergent series converges and, if one series has all negative terms and the other all positive terms, their indicated sum may be a convergent alternating series and not have its terms monotonically decreasing. The series
![]()
is such a series.
James and James. Mathematics Dictionary.
Convergence and divergence of some important series.
Geometric series a + ar + ar2 + ... + arn + ... a and r are constants |
Converges to
if | r | < 1 Diverges if | r |
|
Harmonic series
|
Diverges |
Factorial series
|
Converges to “e” |
p series
|
Converges if p > 1 Diverges if p
|
Binomial series
|
Converges if |x| < 1 Diverges if |x| > 1 |
Necessary condition for the convergence of an infinite series. A necessary condition for the convergence of an infinite series is that the terms approach zero as one goes further out in the series i.e. that the n-th term approaches zero as n becomes infinite. This is not a sufficient condition for convergence; e.g. the series
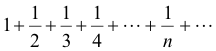
is divergent, although 1/n approaches zero as n becomes infinite.
James and James. Mathematics Dictionary.
Cauchy’s condition for the convergence of an infinite series. Cauchy’s condition for the convergence of an infinite series is that the sum of any number of terms can be made as small as desired by starting sufficiently far out in the series. Tech. A necessary and sufficient condition for convergence of an infinite series Σan is that, for any ε > 0 , there exists an N such that
| an + an+1 + ... + an+h | < ε
for all n > N and all h > 0.
James and James. Mathematics Dictionary.
Absolute and conditional convergence of an infinite series.
Theorem 1. A mixed-term series Σun will converge if the corresponding positive series Σ |un | obtained by replacing all terms of the series by their absolute values converges.
Def. Absolute convergence. A series Σun is said to converge absolutely (or to be absolutely convergent) if the corresponding positive series Σ |un | obtained by replacing all terms of the series by their absolute values converges.
Example. The series
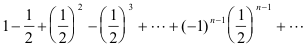
is absolutely convergent since the series
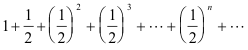
converges.
Def. Conditional convergence. A series is called conditionally convergent if it is convergent, but not absolutely convergent.
Example. The series
![]()
is conditionally convergent since it converges but the series
![]()
diverges..
● If a given series of mixed terms is absolutely convergent then the positive terms alone form a convergent series and the negative terms form a convergent series. If the series of positive terms converges to P and the series of negative terms converges to - Q, then the given series converges to P - Q.
● If a given series is only conditionally convergent, then the positive terms alone form a divergent series and the negative terms form a divergent series.
● An absolutely convergent series remains absolutely convergent, and with the same sum, when the terms are arranged in any other order.
● A conditionally convergent series may become divergent, or may converge to a different sum, if the terms are taken in a different order. Thus the series
![]()
is merely a rearrangement of the series
![]()
It can be shown that the first series is convergent and its sum is half that of the second series. The terms of a conditionally convergent series may in fact be rearranged so as to make the value of the series any desired quantity.
Middlemiss. Differential and Integral Calculus.
Oakley. The Calculus. p. 188
Addition of infinite series. Addition of infinite series is performed by adding corresponding terms i.e. the sum of two infinite series is defined as the series obtained by adding the corresponding terms of the two series. Thus the sum of the series
a1 + a2 + a3 + .... + an + ...
and
b1 + b2 + b3 + .... + bn + ... ,
is the series
(a1 + b1) + (a2 + b2) + (a3 + b3) + .... + (an + bn) + ... .
If two convergent series of constant terms,
a1 + a2 + a3 + .... + an + ...
and
b1 + b2 + b3 + .... + bn + ... ,
have sums S and S', then the series
(a1 + b1) + (a2 + b2) + (a3 + b3) + .... + (an + bn) + ...
converges and has the sum S + S'. If the series
u1 + u2 + u3 + .... + un + ...
and
v1 + v2 + v3 + .... + vn + ... ,
whose terms are functions of x, converge in certain intervals, the term by term sum of these series, namely
(u1 + v1) + (u2 + v2) + (u3 + v3) + .... + (un + vn) + ...
converges in any interval common to the two intervals.
James and James. Mathematics Dictionary.
Multiplication of infinite series. If Σan and Σbn are any two series, their product is defined as the series Σcn
Σcn = a1b1 + (a1b2 + a2b1) + (a1b3 + a2b2 +a3b1) + ... + (a1bn + a2bn-1 + ... + anb1) + ...
If one multiplies together two convergent series having sums U and V, respectively, the resulting series will converge with sum U V if at least one of the series is absolutely convergent. If both series are only conditionally convergent the product series may be divergent.
A power series converges absolutely within its interval of convergence; hence two power series can always be multiplied, and the result will be valid within their common interval of convergence.
Def. Power series. A series whose terms contain ascending positive integral powers of a variable, a series of the form
a0 + a1x + a2x2 + ... + anxn + ...
where the a’s are constants and x is a variable; or a series of the form
a0 + a1(x - h) + a2(x - h)2 + ... + an(x - h)n + ... ,
James and James. Mathematics Dictionary.
Approximation of the sum of an infinite series and estimation of error. Suppose a series Σun converges to sum S. Suppose we wish to approximate its sum by using the partial sum Sk of the first k terms. We need to have some idea of the maximum error we incur by using only the first k terms. Let
Rk = S - Sk.
Rk then is the remainder after k terms. We wish estimates of Rk..
1. Convergent alternating series. For a convergent alternating series,
|Rk| < uk+1
i.e. Rk is less than the first neglected term. Moreover, Rk is positive when k is even and negative when k is odd.
2. Convergent geometric series. For the convergent geometric series Σarn,
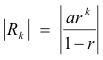
3. Positive series that converges by Integral Test. If the positive series Σun converges by the Integral Test, then
![]()
4. Positive series. Let Σun be a series of positive terms such that
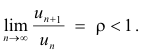
Let Sk be the partial sum of the first k terms and let the condition
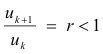
be satisfied for term k and let
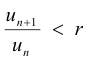
for all n > k. Then
![]()
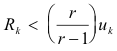
i.e. the error, or remainder after k terms, is less than r/(1 - r) times the last term retained.
Middlemiss. Differential and Integral Calculus. p. 407
Ayres. Calculus (Schaum). p.234
References.
James and James. Mathematics Dictionary.
Middlemiss. Differential and Integral Calculus.
Ayres. Calculus (Schaum).
Oakley. The Calculus (COS).
Spiegel. Advanced Calculus (Schaum).
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life