Centers of the quadric surfaces

SolitaryRoad.com

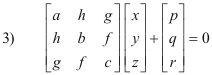
Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

CENTERS OF THE QUADRIC SURFACES

Def. Symmetric geometric configuration. A geometric configuration (curve, surface, etc.) is said to be symmetric (have symmetry) with respect to a point, a line, or a plane, when for every point on the configuration there is another point of the configuration such that the pair is symmetric with respect to the point, line or plane. The point is the center of symmetry; the line is the axis of symmetry, and the plane is the plane of symmetry.

James & James. Math. Dictionary,

“symmetric geometric configurations”

A set of points is symmetrical with respect to a plane (or line or point) if and only if corresponding to any point of the set there is a point symmetrical to it with respect to the plane (or line or point).

Olmstead. Solid Anal.Geometry. p. 96

Center. Usually center of symmetry, such as the center of a circle, or the center of a regular polygon as the center of the inscribed circle.

James & James Math. Dictionary

There are 17 quadric surfaces. In general, these surfaces have various points of symmetry, lines (or axes) of symmetry and planes of symmetry. Of these 17 surfaces only three or four have centers in the usual sense of the word. Those are the real ellipsoid, the hyperboloid of one sheet, the hyperboloid of two sheets and perhaps the real quadric cone. However, a definition of a “center” for a quadric surface has been introduced which, with its mathematical implementation, provides “centers” to all of the 17 surfaces except three. The three exceptions are surfaces 7, 8 and 14 --- the elliptic paraboloid, the hyperbolic paraboloid and the parabolic cylinder. The definition we refer to is this:

Def. Center of a quadric surface. A center of a quadric surface is a point P_c with the property that any line through P_c

(i) determines a chord of the surface whose midpoint is P_c

(ii) has no point in common with the surface,

(iii) lies entirely in the surface.

For the general equation of the second degree

1) f(x, y, z) = ax² + by² + cz² + 2fyz + 2gxz + 2hxy + 2px + 2qy + 2rz + d = 0

those points meeting the above definition of center is given by the solution to the following set of equations

ax + hy + gz + p = 0

2) hx + by + fz + q = 0

gx + fy + cz + r = 0

or in matrix form

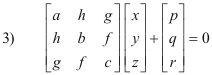
where we recognize the matrix e

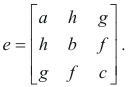
This system of equations provides a single center for six of the quadric surfaces, namely, surfaces 1- 6 --- the ellipsoids, hyperboloids and cones. These six surfaces are called the central quadrics. It provides a line of centers for surfaces 9 - 13 — the elliptic and hyperbolic cylinders and intersecting planes (where the line of centers correspond to their axis of symmetry). And it provides a plane of centers for surfaces 15 - 17 — the parallel and coincident planes. It provides no centers for surfaces 7, 8 and 14 — the paraboloids and parabolic cylinder.

If system 2) provides a center it provides exactly one center, a line of centers, or a plane of centers according as the rank of matrix e

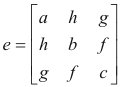
is 3, 2 or 1.

The center or centers of a quadric surface are also given by the following equations:

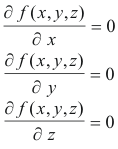
Computing these derivatives we obtain the system

ax + hy + gz + p = 0

hx + by + fz + q = 0

gx + fy + cz + r = 0

which is the same system as 2) above.

Centers of the central quadrics. The center of a central quadric can also be computed from

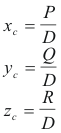
where P, Q, R, D are the cofactors of the elements p, q, r, d in the matrix E

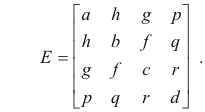
Note on the motivation for the definition of a center of a quadric surface. The motivation for the above definition of the center of a quadric surface is presumably this: This definition and the system of equations 2) which corresponds to it do in fact provide those points at which the first degree terms in 1) above (i.e. 2px, 2qy, 2rz) vanish upon the appropriate translation of coordinate system. Thus the definition of “center” has been so defined as to consist of exactly those points to which translation of the coordinate system must be made in order to reduce the surface to canonical form. It was presumably this consideration that shaped the definition rather than considerations of what one might think of as a “center of symmetry”.