Applications: areas, volumes of solids of revolution, length of a curve, areas of surfaces of revolution, work, fluid pressure

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

APPLICATIONS: AREAS, VOLUMES OF SOLIDS OF REVOLUTION, LENGTH OF A CURVE, AREAS OF SURFACES OF REVOLUTION, WORK, FLUID PRESSURE

I Computation of area — rectangular coordinates. The area bounded by the curve y = f(x), the x-axis, and the ordinates at x = a and x = b is given by the value of

Example 1. Compute the area bounded by the curve

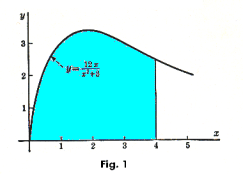
the x-axis, and the ordinates at x = 0 and x = 4. See Fig. 1.

Solution.

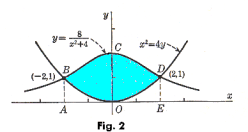
Example 2. Find the area enclosed by the curves

and 4y = x². See Fig. 2.

Solution. The curves intersect at ( 2, 1). If A is the area enclosed by them, then

A = area ABCDE - area ABODE

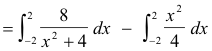
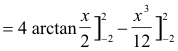
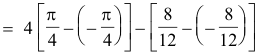
When integration leads to an inverse trigonometric function, as in this example, one should always use the principal values.

Curve defined by parametric equations. Suppose a curve is defined by the parametric equations

x = h(t)

y = g(t)

and we wish to find the area beneath it, the x-axis and the ordinates at between x = a and x = b. Then

dx = h'(t)dt

and the area is given by

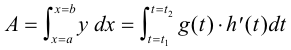
where the limits t₁ and t₂ are the values of t corresponding to x = a and x = b, respectively. They may be obtained from the equation x = h(t).

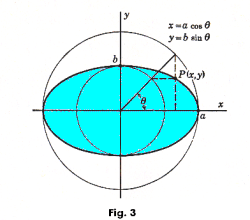
Example. Compute the area of the ellipse x = a cos θ, y = b sin θ. See Fig. 3.

Solution. We will find the area of the first quadrant and multiply it by 4. Since dx = (-a sin θ)dθ, we have

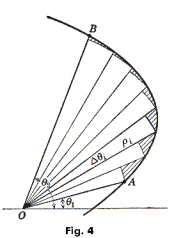
II Computation of area — polar coordinates. In rectangular coordinates we find the area bounded by the curve y = f(x), the x-axis, and the ordinates at x = a and x = b. The corresponding problem in polar coordinates is that of determining the area bounded by the curve ρ = f(θ) and the two radius vectors θ = θ₁ and θ = θ₂. In Fig. 4 this is the area bounded by the curve and the lines OA and OB.

The procedure is as follows: We divide the θ-interval from θ = θ₁ to θ = θ₂ up into n subintervals (not necessarily equal) having the magnitudes Δθ₁, Δθ₂, ... ,Δθ_n. We then draw the corresponding radius vectors, denoting their lengths by ρ₁, ρ₂, ... , ρ_n, and draw the circular arcs as shown.

Remembering that the area of a circular sector having radius r and central angle α is ½ r²α , we write down the following expression for the sum of the areas of the circular sectors:

The area bounded by the curve and the lines OA and OB is then equal to the limit of the following sum

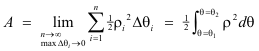
where we are requiring that the largest Δθ_i → 0 as n → ∞.

Theorem. The area bounded by the curve whose polar equation is ρ = f(θ) and the two radius vectors θ = θ₁ and θ = θ₂ is given by

In general, when we perform an integration using this theorem we replace ρ in the integrand with f(θ). The area A will be positive (assuming ρ is real) if the integration is in the counterclockwise sense i.e. if θ₁ < θ₂. If it is performed in the clockwise sense, θ₁ > θ₂, the value of the integral will be negative.

Example 1. Find the area that is common to the circle ρ = 3 cos θ and the cardioid ρ = 1 + cos θ. See Fig. 5.

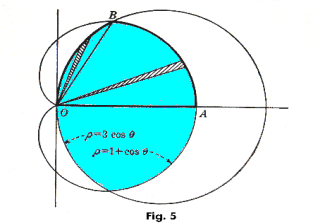
Solution. The curves intersect at the origin and at polar coordinates ( 3/2, π/3). The required area is twice the area bounded by OA, arc AB of the cardioid, and arc BO of the circle. The area bounded by the radius vectors OA and OB and arc AB of the cardioid is given by

The area bounded by radius vector OB and arc OB of the circle is given by

Adding these up and doubling the result, we find that A = 5π/4.

One can think of the area as being generated by the shaded “differential area element” shown in the figure revolving in a counterclockwise fashion. From θ = 0 to θ = ⅓π the outer end of the element is on the arc AB of the cardioid; from θ = ⅓π to θ = ½π the outer end is on arc BO of the circle.

Example 2. Compute the area bounded by the curve ρ = a sin 3θ. See Fig. 6.

Solution. If we want we can compute the area of one leaf by integrating from θ = 0 to θ = ⅓π, and then multiply by 3:

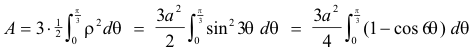
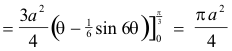
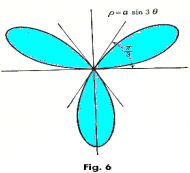
Alternatively, we could have obtained the area by integrating from θ = 0 to π. Thus

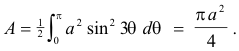
Volumes of solids of revolution.

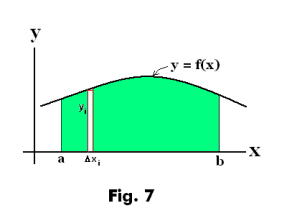
Disk method. Let us suppose the area shown in green in Fig. 7, bounded by the curve y = f(x), the x-axis, and the ordinates at x = a and x = b, is revolved about the x-axis so as to create the barrel shaped solid shown in Fig. 8. We wish to find the formula for the volume of the solid thus generated.

Derivation of the formula. If the rectangle with base Δx_i and height y_i shown in Fig. 7 is revolved about the x-axis it generates a cylindrical disk of radius y_i and thickness Δx_i whose volume is πy_i²Δx_i. If the interval [a, b] is partitioned into n subintervals, then the sum of the volumes of the n disks thus generated is

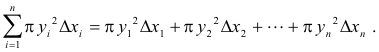
The volume of the solid is then given by

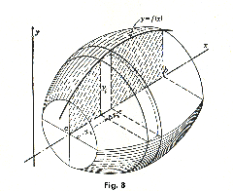
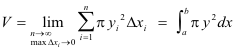
Theorem 1. If the area bounded by the curve whose equation is y = f(x), the x-axis, and the ordinates at x = a and x = b is revolved about the x-axis, the volume generated is given by

Similarily, if the area bounded by the curve x = f(y), the y-axis, and the lines y = c and y = d is revolved about the y-axis, the volume generated is given by the formula

Example. Compute the volume generated by revolving the area bounded by the y-axis and the parabola y² - 4y + 2x - 5 = 0 about the y-axis. See Fig. 9.

Solution. Setting x = 0 and solving for y, we find that the parabola crosses the y-axis at y = -1 and y = 5. The volume is given by

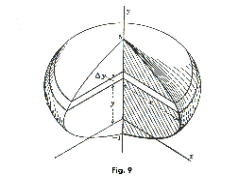
The cylindrical shell method. There is another method for computing volumes of surfaces of revolution that is in some cases simpler than the disk method. Consider the solid of revolution shown in Fig. 10 obtained by revolving one arch of the sin function y = sin x about the y-axis. If we chose to use the disk method in computing the volume, each disk would have a hole in it (it would look like a washer). A simpler method is to revolve each vertical strip, base Δx_i and height y_i, about the y-axis generating a thin cylindrical shell of inside radius x_i, height y_i, and

thickness Δx_i as shown in the figure. The volume of such a shell is approximately equal to (2πx_i)y_iΔx_i. If we partition the interval [a, b] on the x-axis over which we wish to integrate into n subintervals then the sum of the volumes of the cylindrical shells is given approximately by

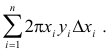
The volume of the solid is then given by

Theorem 2. Let an interval [a, b] on the x-axis be on one side of the origin or the other, but not overlapping it, and let a < b. If the area bounded by the curve whose equation is y = f(x), the x-axis, and the ordinates at x = a and x = b is revolved about the y-axis, the volume generated is given by

The type of analysis, way of thinking, that we have just employed can be used to find volumes for a diverse assortment of volume-of-revolution type problems.

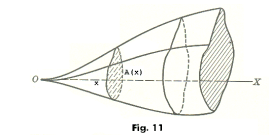
Volumes of solids with known cross sections. Suppose we have a solid whose cross sections perpendicular to the x-axis have areas that are functions of the variable x i.e. the area of the cross section at distance x from the origin is given by A(x). See Fig. 11. In this case the volume of the solid is given by

Note that the disk method of computing volumes is a special case of this method. The disk method amounts essentially to viewing the solid as being made up of thin slices created by passing parallel planes perpendicular to its axis. In the disk method A(x) = πy².

Example. Consider the conoid shown in Fig. 12. Its base is the circle x² + y² = r² and its “vertex” is a line segment parallel to the base, at a distance h above it, and of length 2r. The surface is generated by an element that moves so as to intersect both the circle and this line segment and remain parallel to the yz-plane.

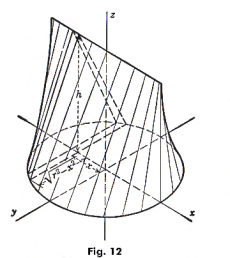
At a distance x from the yz-plane, the section of this solid is a triangle whose base is and whose altitude is the constant h. The area of this section, expressed in terms of x, is

The volume of the conoid is then given by

Length of a curve.

Rectangular coordinates.

Differential of arc length. The differential of arc length ds is given by

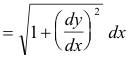
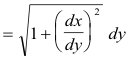
Length of a curve. The length of a segment of a curve is given by

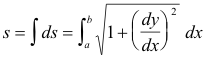
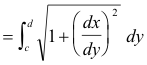
Polar coordinates.

Differential of arc length.

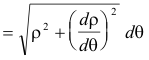
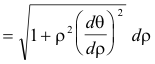
Length of a curve.

******************************************

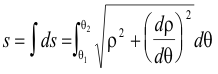
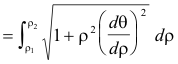
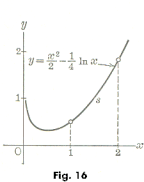
Example 1. Find the length of the curve

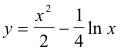
between points for which x = 1 and x = 2. See Fig. 16.

Solution. Since

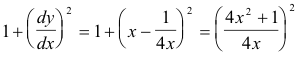
we have

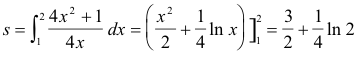
Example 2. Compute the perimeter of the circle ρ =2a sin θ. See Fig.17.

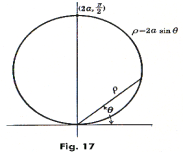
Solution. Since

we have

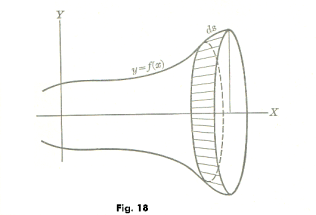
Area of a surface of revolution. When the curve y = f(x) is revolved about the x-axis, a surface is generated. See Fig. 18. To find the area of this surface we consider the area generated by an element of arc ds. The area generated by an element of arc ds is given by

dS = 2πy ds.

Summing all such elements of surface area we get

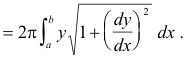
Example. Compute the area of the spherical surface generated by revolving the upper half of the circle x² + y² = r² about the x-axis.

Solution.

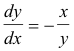
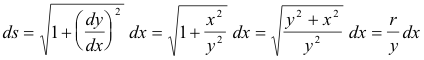
Work. Let a body move along a straight line under the application of a constant force. The product of the magnitude of the force and the distance moved is called the work done on the body during the motion. In symbols, the work done is given by the formula

W = Fd

where W is the work done, F is the applied force, and d is the distance moved. Thus the work done by the 20 lb. force indicated in Fig. 19 in pushing the block a distance of 12 ft. is 20(12) = 240 ft-lbs.

Work done by a variable force acting along a curve. Let us now generalize our notion of work to consider a variable force acting in the direction of motion which takes place along some curve C. The distance along the curve from some fixed initial point A to some point P is s. The differential element is ds. If the force F is a function of s, then the differential element of work done will be dW = F(s) ds. Summing all such elements we get the total work done between points S₁ and S₂ on the curve:

Example. The force required to stretch a spring is directly proportional to the elongation. If a force of one pound stretches the spring half an inch, what is the work done in stretching the spring 2 inches?

Solution. Call L the natural length of the spring and x the elongation. The applied force F and elongation x are related by F = kx where k is the constant of the spring. First we must find the value of k. Plugging our given values for F and x into F = kx we get

k = 2.

Hence F = 2x and the work done is

Fluid pressure. At any point in a fluid there exists a pressure (say, lbs./sq. ft.) arising from the weight of the fluid above it. Envision a vertical column of liquid 1 ft. x 1 ft. in cross section. The pressure in lbs./sq. ft. at any point in the column is due to the weight of the liquid above it. Just as a stack of cement blocks exerts a pressure on the surface beneath it, even so a column of fluid exerts a pressure. The formula giving this pressure is

p = wh

where p is the pressure at the point, h is the depth below the surface, and w is the density of the fluid (i.e. weight of the fluid per unit volume).

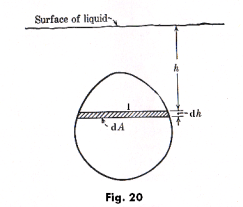
Problem. Compute the total force exerted by a fluid on one side of a vertical surface (such as, for example, a vertical side of a dam) submerged in the fluid.

Solution. Consider the submerged vertical surface shown in Fig. 20. Consider a horizontal strip of length l and depth h on this surface as shown in the figure. Let this strip be of width dh. Then the area dA of the strip is l dh and the pressure on it is wh. The force exerted by the fluid on this strip is pressure x area or dF = wh dA = whl dh. Therefore the total force exerted by the fluid on the submerged vertical surface will be given by

This integral can be evaluated once l is expressed as a function of h, l = f(h).

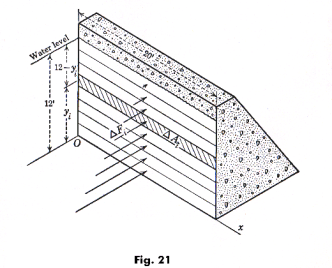
Example 1. Given the dam shown in Fig. 21. The dam is 20 ft. long. Find the total force exerted against the face of the dam when the water in 12 ft. deep.

Solution. The area of a strip is given by

dA = 20 dy (sq. ft.)

In the coordinate system shown in the figure the depth of the strip below the water surface is “12 - y” ft. and the pressure at this depth is w(12 - y) lbs./sq. ft. The pressure against the strip is then

wh dA = w(12 - y)(20 dy) lbs.

The total force against the face of the dam is then

References.

Middlemiss. Differential and Integral Calculus.

Oakley. The Calculus.

Smith, Salkover, Justice. Calculus.