Website owner: James Miller
INDETERMINATE FORMS, L’HOPITAL’S RULE
The indeterminate forms 0/0 and ∞/∞. If two functions f(x) and g(x) both become zero at x = a, or if both become infinite as x approaches a, their quotient f(x)/g(x) is without meaning when x = a. In the first case the fraction is said to assume the indeterminate form 0/0 when x = a; in the second case it is said to assume the indeterminate form ∞/∞ when x approaches a. An example that occurs frequently is the indeterminate form 0/0 assumed by Δy/Δx when Δx approaches zero in the definition of the derivative.
The indeterminate forms 0/0 and ∞/∞ may arise when x becomes infinite as well as for some finite value of x. Thus if f(x) or g(x) both become zero or become infinite as x becomes infinite, the fraction f(x)/g(x) assumes one of the indeterminate forms 0/0 or ∞/∞.
Def. Indeterminate form. An expression of type
![]()
Such expressions are undefined. They arise in various ways, especially when replacing different members of composite functions with their limits.
L’Hopital’s Rule. If the fraction f(x)/g(x) assumes one of the indeterminate forms 0/0 or ∞/∞ when x = a, then
![]()
A similar statement holds if the indeterminate form arises when x becomes infinite instead of when x = a.
If f '(x)/g'(x) also assumes an indeterminate form of the type 0/0 or ∞/∞, the rule can be applied likewise to it. The process can, in fact, be repeated as many times as necessary to yield a fraction f(n)(a) / g(n)(a) which is not indeterminate.
Proof. For the case of indeterminates of form 0/0, L’Hopital’s rule follows directly from Cauchy’s Generalized Mean Value Theorem which states that if f(x) and g(x) are differentiable functions over an open interval (a, b) then
![]()
Write x for b in 1) and it becomes
![]()
Then, since f(a) = g(a) = 0, equation 2) becomes
![]()
Now taking limits of both sides and noting that as x approaches a, x1 also approaches a
![]()
L’Hopital’s rule can be proved in general under the assumption that there exists a neighborhood U of a in which f and g are both differentiable, except possibly at a, and there is no point of U at which f ' and g' are both simultaneously zero.
Example 1. Evaluate
![]()
Solution. When θ = 0, both numerator and denominator are zero. Thus it is of type 0/0 and the rule applies.
![]()
Example 2. Evaluate
![]()
Solution. When x = 2, both numerator and denominator are zero, it is of type 0/0, and the rule applies.
![]()
The indeterminate form 0 • ∞. If f(x)g(x) assumes the indeterminate form 0 • ∞ when x has a finite value a, or when x becomes positively or negatively infinite, the product may be converted to one of the indeterminate forms 0/0 or ∞/∞ by use of the identities
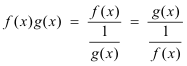
and hence may be investigated by one of the foregoing rules.
Example. Evaluate
![]()
Solution. Since csc x ln(x + 1) assumes the form ∞∙0 for x = 0, we write
![]()
This assumes the form 0/0 for x = 0. Hence by L’Hopital’s rule
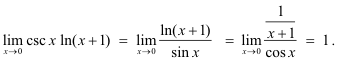
The indeterminate form ∞ - ∞. An indeterminate form of type lim (f - g) = ∞ - ∞ can be transformed into a type 0/0 using the algebraic identity
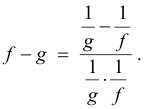
Example. Evaluate
![]()
Solution. This is of type ∞ - ∞.
![]()
using L”Hopital’s Rule
![]()
Indeterminate forms 1 ∞, 00, ∞0. If
![]()
takes on one of the indeterminate forms 1 ∞, 00, ∞0 , then taking the logarithm will convert it into a type 0∙∞. Then from a type 0∙∞ we can convert it into a type 0/0 or ∞/∞. Let us illustrate with an example. Suppose
![]()
Taking the logarithm we have
![]()
Now we convert it to a 0/0 type by using
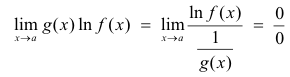
and then apply L’Hopital’s Rule. [Or, alternatively , we can write
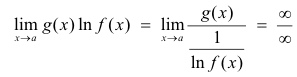
and apply the rule if this form is easier to handle as far as the differentiation is concerned.]
If
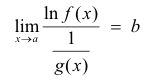
then the limit desired is
![]()
We can treat type
![]()
in a similar way since
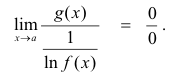
And again the method applies to type
![]()
since
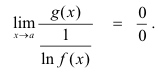
Summary.
To find lim fg which assumes an indeterminate form of type 1 ∞, 00, ∞0 apply L’Hopital’s rule to
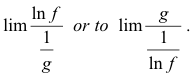
If L’Hopital’s Rule applied to one of these yields b for a limit, then lim fg = eb.
Example. Evaluate
![]()
Solution. This is of type 1∞. Applying L’Hopital’s Rule to
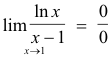
gives
![]()
so the required limit is
![]()
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life