Website owner: James Miller
TANGENTS, NORMALS, PARAMETRIC EQUATIONS, VECTORS, CURVILINEAR MOTION, VELOCITY, ACCELERATION, RELATED TIME-RATES PROBLEMS

Equation of the tangent to a curve. Suppose we have a curve C defined either by y = f(x) or, more generally, f(x, y) = 0. Let P0(x0, y0) be a point on the curve at which the derivative dy/dx exists. Then the equation of the tangent to the curve at point P0 is
1) y - y0 = m(x - x0)
where m = dy/dx at P0. See figures 1 and 2.
Normal to a curve. A normal to a curve at a point is a line perpendicular to the tangent at the point. See Fig. 3. Given a curve C and a point P0(x0, y0) on the curve at which the derivative dy/dx exists, the equation of the normal to a curve at point P0 is
![]()
where m = dy/dx at P0.
We now present the following definitions:
Length of tangent. Line segment P0T in Fig. 4 (i.e. distance from the point of tangency to the intersection with the x axis).
Length of normal. Line segment P0N in Fig. 4.
Subtangent. Line segment TS in Fig. 4 (i.e. projection of line segment P0T on x axis).
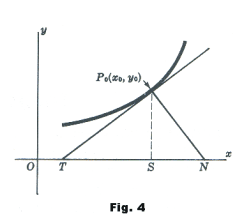
Subnormal. Line segment SN in Fig. 4 (i.e. projection of line segment P0N on x axis).
The lengths of these quantities are given by
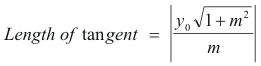
![]()
Length of subtangent TS = |y0/m|
Length of subnormal SN = |my0|
where m is the slope dy/dx at point P0.
Angle of intersection of two curves. The angle of intersection of two curves is defined as the angle between the tangents to the curves at their point of intersection. This angle is given by the formula
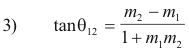
where θ12 is the angle measured counterclockwise from the tangent to curve 1 to the tangent to curve 2 and m1 and m2 are the slopes of the tangents.
Parametric equations of a curve. If the coordinates (x, y) of a point P on a curve are given as functions
x = f(u)
y = g(u)
of a third variable or parameter u, the equations x = f(u), y = g(u) are called parametric equations of the curve. Such a curve can be plotted point by point by giving successive values to the parameter u, each value determining a point on the curve. Any equation can be written in an unlimited number of parametric forms, since the parameter can be replaced by an unlimited number of functions of the parameter. If it is possible to eliminate u from the parametric equations, the elimination yields the equation of the curve in the usual form in which x and y are the only variables, that is, the rectangular or cartesian equation of the curve. However, the cartesian form, if obtainable, may be very complicated and it is often simpler to deal with the parametric form. The parametric form is often the most natural form in which to express the relationship between variables.
Finding derivatives when equations are in parametric form.
First derivative. The derivative dy/dx is given by
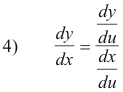
which is derived directly from the chain rule
![]()
Second derivative. The derivative d2y/dx2 is given by
![]()
Vectors and their components. A quantity, such as time, temperature, density or volume, that can be completely specified by means of a real number is called a scalar quantity. A quantity, such as force or velocity, that requires the specification of both its magnitude and its direction in order to characterize it completely is called a vector quantity.
A vector quantity can be represented by an arrow or vector. The length of the vector represents the magnitude of the quantity and the direction of the arrow gives the direction of the quantity.
Suppose a particle has a velocity of 100 ft. per minute in a direction 30o north of due east. We could then represent its velocity by the vector AB shown in Fig. 5. If the particle maintained this velocity for 1 minute it would travel 100 ft. in the direction AB. Thus it would move
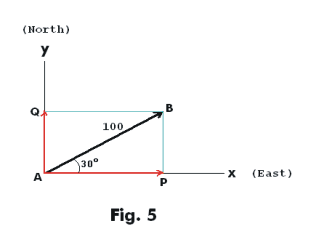
100 cos 30o = 86.6 ft. east,
and
100 sin 30o = 50 ft. north.
In the figure the projections AP and AQ of the vector AB represent the components of the velocity in the x and y directions.
In general, if we have some vector whose magnitude is v and whose direction is given by the angle θ that it makes with the x-axis, then its components along the axes have the magnitudes
vx = v cos θ
vy = v sin θ.
Conversely, the magnitude and direction of a vector having components vx and vy along the axes are given by
![]()

Curvilinear motion. Velocity and acceleration. Let us suppose that a point moves in the xy-plane in such a way that its coordinates at any time t are given by the parametric equations
x = g(t)
y = h(t).
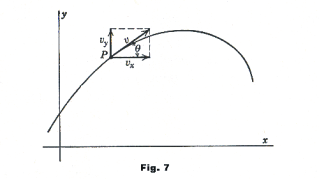
Then its component of velocity in the x direction is given by dx/dt and its component of velocity in the y direction is given by dy/dt. The value of dx/dt at any instant is the time rate at which the x-coordinate is changing; i.e., it is the rate at which the projection of the point on the x-axis is moving along this axis. Similarly for dy/dt.
Let
vx = dx/dt
vy = dy/dt .
Then the magnitude and direction of the velocity are then given by
![]()
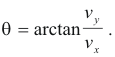
Observe that, since
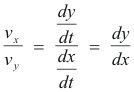
the direction of the velocity vector is that of the tangent to the path (see Fig. 7).
Similarly for the x- and y-components of acceleration we have
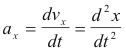
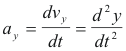
The magnitude and direction of the acceleration are then given by
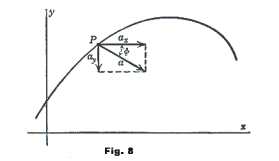
![]()
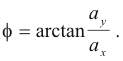
The acceleration vector is not, in general, tangent to the curve of motion. It is in fact always directed toward the concave side of the path and is normal to the path if the speed of the moving point is constant. See Fig. 8.
Example. A point moves in the xy-plane so that at any time t its coordinates are
x = t2 - 2
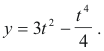
Compute the magnitude and direction of its velocity and acceleration when t = 2. Find the Cartesian equation of its path.
Solution.
vx = dx/dt = 2t
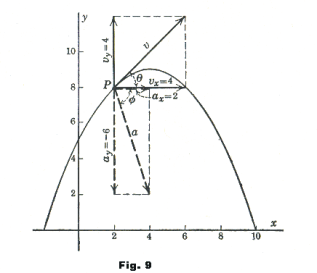
vy = dy/dt = 6t - t3
vx]t=2 = 4
vy]t=2 = 4
![]()
θ = arctan 1
ax = d2x/dt2 = 2
ay = d2y/dt2 = 6 - 3t
ax]t=2 = 2
ay]t=2 = -6
![]()
![]()
If we eliminate t from our two equations we find that the path described by the moving point is the parabola
4y = 20 + 8x - x2.
Fig. 9 shows the position of the point on the path when t = 2 and the vectors representing vx, vy, v and ax, ay, a.
.
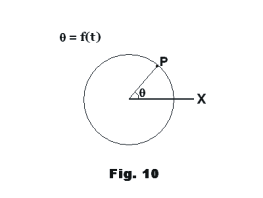
Circular motion. Angular velocity, Angular acceleration. Let a particle P move along the circumference of a circle with its position at any time t given by θ = f(t) where θ is the angle (in radians) as measured from the polar axis of a polar coordinate system with origin at the center of the circle. See Fig. 10. Then the angular velocity and angular acceleration of the particle P are defined as follows:
Angular velocity. The angular velocity ω at time t is given by
![]()
Angular acceleration. The angular acceleration α at time t is given by
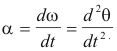
We will now consider a certain genre of problems that are known as “related rates” or “related time-rates” problems.
Related time-rates problems. Suppose two variable quantities x and y, both depending on time, t, are connected by some relation [like by some equation g(x, y) = 0]. Problem: The time rate of change of one of the variables is known and the time rate of change of the other is to be found. For example, the time rate of change of x , dx/dt, may be known and the corresponding time rate of change of y, dy/dt, is to be found. Since dx/dt and dy/dt are connected by an equation they are called related time-rates.
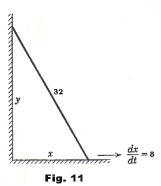
Example 1. A ladder 32 ft. long rests against a wall and the lower end is being pulled out from the wall at 8 ft. per minute. At what rate is the top descending at the instant when the lower end is 9 ft. from the wall?
Solution. Denote by x and y the distances of the bottom end of the ladder from the wall and the top end from the ground. See Fig. 11. The variables x and y are connected by the relation
1) x2 + y2 = 322.
We are given dx/dt = 8, and we wish to find the value of dy/dt at the instant when x = 9. Differentiating 1) with respect to time we get
![]()
Thus,
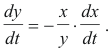
At the instant when x = 9, the value of y is 30.7 feet and dx/dt = 8; hence,
![]()
The negative sign indicates that y is decreasing. The upper end of the ladder is dropping down at the rate of 2.3 feet per minute.
Example 2. Water is running out of a conical funnel at the rate of 2 in3/sec. The funnel is 10 in. in diameter and 10 in. deep. Find the rate at which the water level is dropping when it is 3 inches from the top.
Solution. See Fig. 12. Let x be the radius and y be the height of the surface of the water at time t and let V be the volume of water in the funnel at time t. We must first express the volume V of water in the cone in terms of its depth y. We are given that dV/dt = -2 in3/sec and must compute the value of dy/dt at the instant when y = 7 in. Now
![]()
and
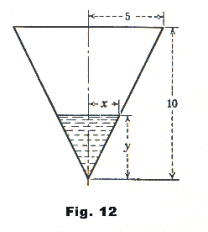
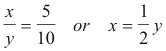
so
![]()
Differentiating with respect to t
![]()
Thus
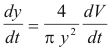
At the instant when y = 7
![]()
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life