Website owner: James Miller
FUNCTIONS, CONTINUITY

The two central concepts of calculus are the concept of the derivative of a function and the concept of the integral of a function. Basic to these two concepts is the concept of a function. The concept of a function is one of those mathematical concepts which have gone through a succession of re-definitions, becoming more and more broad, general and abstract with each re-definition. The concept is one of the most important in mathematics, occurring in many different ways and settings. When one attempts to take a concept that occurs in many ways and forms and create a single definition that covers all cases things can get lost from the broadness. We will present the concept as applied to calculus.
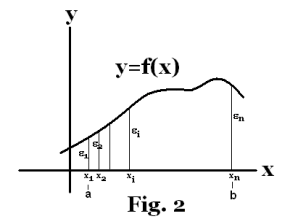
A variable y is said to be a function of a variable x, written y = f(x), if for each value that x can assume there is a corresponding value for y. The concept of a function y = f(x) is most easily understood by considering its graph in a Cartesian coordinate system. In Fig. 1 a variable y is depicted as a function of a variable x. The variable x is the independent variable and the variable y is the dependent variable. Now consider Fig. 2. As x progresses from point a to b on the x axis, passing through successive values x1, x2, x3, ... , xn, the values of y = f(x) progress through values ξ1, ξ2, ξ3, ... ,ξn. The central idea is that as the independent variable x ranges over some range of values from some set, the dependent variable y varies, assuming a succession of values.
The variable to which values are assigned is called the independent variable. The other variable whose values are determined by the value of the independent variable is called the dependent variable. Saying that y is a function of x is equivalent to saying that y depends on x.
An important characteristic of a function is that for each value of the independent variable x, the dependent variable y assumes one and only one value. This property is essential to the concepts of derivative and integral in calculus.
We now give a more formal definition of a function:
A variable y is said to be a function of a second variable x if by some rule, device or means there is assigned to each of a certain set of values of x a single value for y.
This definition is not our final definition, but it is a simple one, gives the main thrust of the concept, and will serve for present. Let us consider some examples of functions.
Examples of functions.
1] The formula for the area of a circle, A = πr2, gives the area A of a circle as a function of the radius r. To each value of r there corresponds a value for A.
2] The equation
y = 5x2 + 3x + 2
is a function. It gives a value of y for each value of x in the interval consisting of the entire x axis.
● In general, any equation or formula that gives the value of one variable in terms of another represents a function.
3] A chart showing the air temperature at some point in space as measured over some period of time defines a function of temperature v.s. time for that location.
● We see from this last example that a function need not be defined by some formula or analytic expression. It can be defined by some chart, graph, or table.
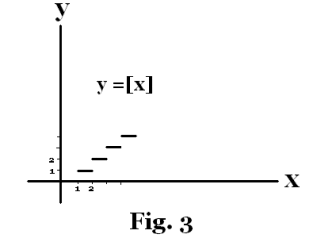
4] Let [x] represent the integral part of a real number i.e. the integer obtained by truncating the fractional part. For example, [2.1] = 2, [5.4] = 5 , etc. Then y = [x] is the function shown in Fig. 3.
Domain of definition of a function. In general, the independent variable is defined over some set of values. There are frequently restrictions, either implied or stated, on the values that may be assumed by the independent variable. The set of values over which the independent variable is defined is called the domain of definition of the function.
Example. In the case of the formula for the area of a circle, A = πr2, the range of definition for the independent variable r is the positive numbers. A negative value of r makes no sense.
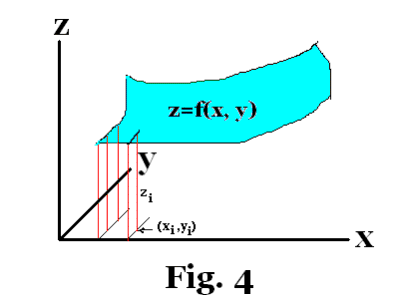
In the definition above we have defined a function for the case of a single independent variable. There can, however, be more than one independent variable. For example, the equation z = 3x2 + 5 sin y + 2 represents such a function. It defines the variable z as a function of independent variables x and y. Fig. 4 shows a function z = f(x, y) where x and y are the independent variables and z is the dependent variable. For each pair (xi, yi) in some delineated portion of the x-y plane there corresponds a zi. In the general case there may be n independent variables giving functions of the type
y = f(x1, x2, ... , xn) .
In this case numerical values are assigned to the n-tuples (x1, x2, ... , xn). The domain of definition of such a function corresponds to that set of points in n-space defined by the ranges (i.e. intervals [ai, bi] ) over which the variables x1, x2, ... , xn are allowed to run. The function f assigns a value to each point in the domain. Thus the definition that we gave above must be modified to accommodate the case of n independent variables. So we now give another broader definition to the term “function”.
Def. Function. A function is an assignment of a numerical value, by some rule, device or means, to each n-tuple (x1, x2, ... , xn) in n-space where n is the number of independent variables.
This definition covers the case of a single independent variable since in that case the domain is 1-space. It is by no means the broadest definition of the concept of a function but it serves our needs.
Functional notation. Symbols such as f, F, g, G, Φ, etc., are used to denote a function, the function values corresponding to x being denoted by f(x), F(x), g(x), G(x), Φ(x), etc. and read as "f of x" or "the f function of x," etc.
Functions and loci. In analytic geometry we are introduced to the concept of the locus of an equation. Let us now compare the concepts of the locus of an equation and the concept of a function. Both concepts utilize a Cartesian coordinate system to depict the relationship existing between variables. In the concept of the locus of an equation there are no independent or dependent variables. All variables have the same status. The locus of an equation is the totality of all points whose coordinates satisfy the equation; it is the solution set of the equation. The solution set is the set of all solutions of the equation. We plot the solution set of an equation in a coordinate system to give ourselves a pictorial representation of the locus (and in our minds often equate the pictorial representation with the locus itself). Every equation has a locus. An equation in a single variable f(x) = 0 has a locus consisting of points on the x axis. An equation in two variables f(x, y) = 0 has a locus consisting of lines, curves or points in the x-y plane. An equation in three variables f(x, y, z) = 0 has a locus consisting of a surface in space. Equations in four or more variables also have loci but we are unable to represent them pictorially in a coordinate system.
In the study of equations the concept of the locus is a powerful one with applicability to all equations. The concept of function, on the other hand, is limited to only certain types of equations in which one variable can be expressed in terms of the others.
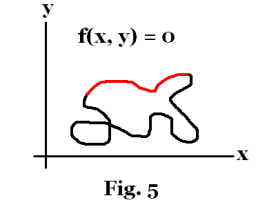
Suppose we have an equation f(x, y) = 0 with the graph shown in Fig. 5. It is obvious by looking at the graph that one would not be able to express either variable x or y as a function of the other since any vertical or horizontal line passing through the graph cuts the graph in more than one point. If a vertical line cuts the graph in two points it means that for that value of x there are two values of y that satisfy the equation. However, one could judiciously select portions of the graph and represent those particular segments as functions of one variable or the other. For example, the segment shown in red could be represented by some function y = g(x).
Now suppose you have an equation f(x, y) = 0 in which one of the variables can be expressed as a function of the other i.e. the equation can be solved for one variable or the other. Say y can be isolated and expressed in terms of x as y = h(x). An example would be the equation
4x2 - 2y + 10 = 0
which can be solved for y to give
y = 2x2 + 5 .
In this case the locus of the equation corresponds to the graph of the function y = h(x). In an equation of this type both concepts apply and one can look at the equation from either point of view — as a locus or as a function.
Much of the power of the concept of a function comes from the fact that any analytic expression in one or more variables can be thought of as a function. Thus the expression
![]()
can be viewed as a function
![]()
We can then plot the function as u = f(x, y) in a Cartesian coordinate system and observe its behavior.
We will now consider the idea of the continuity of a function.
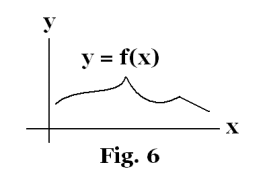
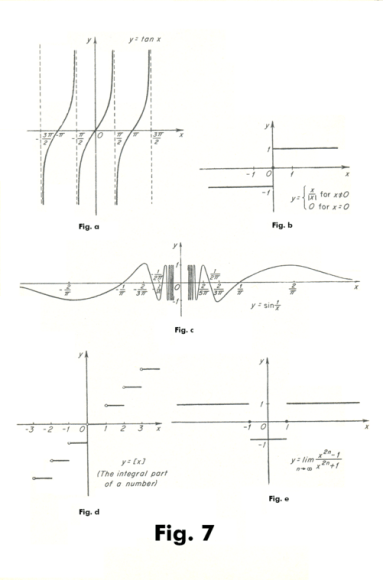
Continuous functions. The general idea of what a continuous function is may be obtained from the fact that its graph is continuous; that is, there are no breaks in the graph. Taking the example of a plane curve, a continuous plane curve is one that can be drawn without lifting the pencil from the paper. The idea underlying continuity is that to a very small change in an independent variable there corresponds a very small change in the dependent variable, or function ( as opposed to a large, abrupt change). Continuous functions are very important in mathematics because mathematics is the language of science and most of the laws of science (in physics, chemistry, etc) represent relationships that are continuous in nature. The relationships are continuous and the quantities involved such as time, distance, area, volume, temperature, force, velocity, etc. are continuous. Figure 6 shows an example of a continuous function. Note that a continuous function may contain sharp corners (sharp changes in direction). Figure 7 shows several examples of discontinuous functions.
To give the formal mathematical condition for the continuity of a function we must introduce the following concept:
Limit of a function f(x) as x approaches a constant. A function f(x) is said to approach b as a limit, when x approaches a, if the value of |f(x) - b| becomes arbitrarily small for values of x sufficiently close to a. This can be written
![]()
which is read “the limit of f(x) as x approaches a is b”.
A function may or may not approach a limit as the variable approaches a limit. And if it does approach a limit, it may approach two different limits according as to whether x approaches a from the right or from the left side. If this happens we designate them
![]()
where x→ a+ means x
approaches a from the right
and x → a- means x approaches a from the left. Examples of different limits being
reached, according to whether x approaches from the right or left, can be seen at the
points of discontinuity in the functions of Fig.7. If a function approaches two different
limits depending on how x approaches a, then
![]() is assumed not to exist i.e. a
function f(x) is said to approach b as a limit, when x approaches a, only if the limit is b no
matter how x approaches a.
is assumed not to exist i.e. a
function f(x) is said to approach b as a limit, when x approaches a, only if the limit is b no
matter how x approaches a.
Important theorems on limits. The following theorems on limits are important:
![]()
![]()
![]()
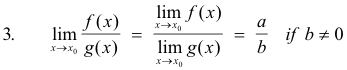
Let us consider an arbitrary function y = f(x) and some specific value x0 of the independent variable. If our function reflects a continuous process, then to values of x which differ only slightly from x0 there will correspond values of the function f(x) differing only slightly from the value f(x0) at the point x0. Thus if the increment x - x0 of the independent variable is small, then the corresponding increment f(x) - f(x0) of the function will also be small. We are thus led to the following definition for the continuity of a function at a point:
Def. Continuity at a point. A function f(x) is said to be continuous at a point x = x0 if f(x0) is defined and if
![]()
● Note that the above condition for continuity implies that f(x) is defined also for a range of values extending on either side of x = x0.
Def. Continuity over an interval. A function f(x) is said to be continuous in a given interval if it is continuous at every point of this interval.
Def. Continuity of a function. A function f(x) is said to be continuous if it is continuous at every point of its domain of definition.
Thus we see that our definition of the continuity of a function is a step-wise process in which we first define local continuity at a point. The definition was introduced by Cauchy.
Addition, subtraction, multiplication and division of continuous functions. If continuous functions are added, subtracted, multiplied, or divided (with the exception of division by zero), the result is a continuous function. Division by zero generally produces a discontinuity. Thus in the function
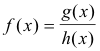
f(x) will generally have a discontinuity at values of x at which h(x) = 0.
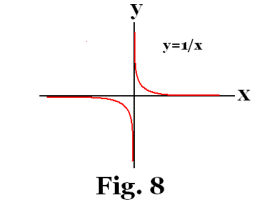
Examples of discontinuous functions. The function y - 1/x, discontinuous at x = 0, is an example a discontinuous function. See Fig. 8. For other examples see Fig. 7. If one examines the functions of Fig. 7 he will note different types of discontinuity. In some cases two different limits are approached by the function, depending on the side from which x approaches the discontinuity. In the case of Fig. 7c no limit is approached when x approaches from either side (the function just oscillates).
The jump-like behavior seen in many discontinuous functions does not only occur in mathematical functions. It can also occur in nature. For example, if one considers the graph of the quantity of heat in a gram of water vs temperature, the graph shows a sharp jump at 0o C.
Removable discontinuities. The function
![]()
is discontinuous at the point x = 2 since f(2) is not defined (both numerator and denominator are zero). This discontinuity, however, is a type that can be removed. Observe that for all values of x except x = 2 we have the identity
![]()
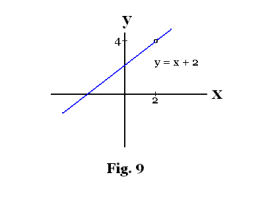
which means that the graph, except for the lack of a point corresponding to x = 2, is simply the straight-line locus of the equation y = x + 2. See Fig. 9. This point of discontinuity can be removed by defining the function as
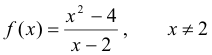
f(2) = 4 .
Removing the discontinuity consists simply of properly filling the “hole”.
Special kinds of functions.
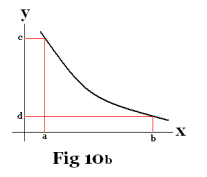
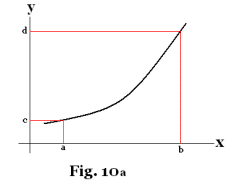
Inverse functions. Let y = f(x) be a function that is either continually increasing on an interval [a, b] or continually decreasing. See figures 10a and 10b. Let c = f(a) and d = f(b). From the figures it is evident that for each value of y on the interval [c, d] there corresponds a single value of x on the interval [a, b]. Thus on the interval [c, d] we have a completely determined function x = g(y). The function x = g(y) is called the inverse function of y = f(x) and vice versa.
Implicit functions.
Def. Implicit function. A function defined by an equation of the form f(x, y) = 0 [in general, f(x1, x2, ... , xn) = 0 ]. If y is thought of as the dependent variable, f(x, y) = 0 is said to define y as an implicit function of x.
James and James. Mathematics Dictionary.
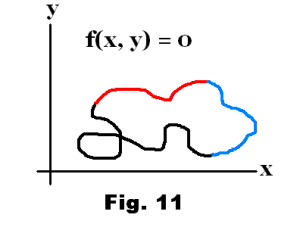
Suppose we have an equation f(x, y) = 0 with the graph shown in Fig. 11. It is obvious by looking at the graph that neither variable could be expressed as a function of the other. In other words, it wouldn’t be possible, by rearranging f(x, y) = 0, to separate out one of the variables and express it as a function of the other. The entire locus of Fig. 11 could not be represented as a single function y = f(x) or x = g(y). It would be possible, however, to judiciously select portions of the graph and represent those particular segments as functions of one variable or the other. For example, the segment shown in red could be represented by some function y = f(x) and the segment shown in blue could be represented by some function x = g(y). It is in this sense that the function f(x, y) = 0 can be thought of as defining y as a function of x or x as a function of y. Given any particular point P on the graph there exists some vicinity around P where either y can be expressed as a function of x or x can be expressed as a function of y. In fact, for most points P on the graph there exists a vicinity around P where one can define a segment on which inverse functions can be defined, y = f(x) and x = g(y).
Often we can solve an equation f(x, y) = 0 for one of the variables obtaining multiple solutions constituting multiple branches. Consider the following example.
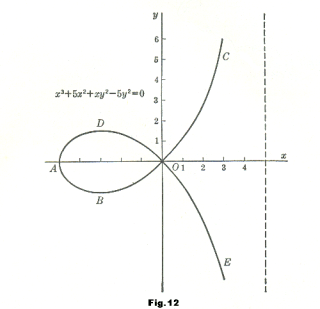
Example. Consider the equation
1) x3 + 5x2 + xy2 - 5y2 = 0
which defines y as an implicit function of x. Its graph is shown in Fig. 12. If we solve 1) for y we get the two solutions
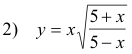
and
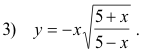
The graph of the first solution is the arc ABOC of the curve (see figure) and the graph of the second solution is the arc ADOE. These two solutions represent two separate functions which, together, constitute the locus of equation 1).
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life