Partial derivative. Total differential. Total derivative. Chain rule. Directional derivative. Differentiation under the integral sign. Leibnitz�s rule.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

PARTIAL DERIVATIVE. TOTAL DIFFERENTIAL. TOTAL DERIVATIVE. CHAIN RULE. DIRECTIONAL DERIVATIVE. DIFFERENTIATION UNDER THE INTEGRAL SIGN. LEIBNITZ’S RULE.

Let us consider a function

1) u = f(x, y, z, p, q, ... )

of several variables. Such a function can be studied by holding all variables except one constant and observing its variation with respect to one single selected variable. If we consider all the variables except x to be constant, then

represents the partial derivative of f(x, y, z, p, q, ... ) with respect to x (the over-bars indicating variables held fixed). The variables held fixed are viewed as parameters.

Def. Partial derivative. The partial derivative of a function of two or more variables with respect to one of its variables is the ordinary derivative of the function with respect to that variable, considering the other variables as constants.

Example. The partial derivative of 3x²y + 2y² with respect to x is 6xy. Its partial derivative with respect to y is 3x² + 4y.

The partial derivative of a function z = f(x, y, ...) with respect to the variable x is commonly written in any of the following ways:

Its derivative with respect to any other variable is written in a similar fashion.

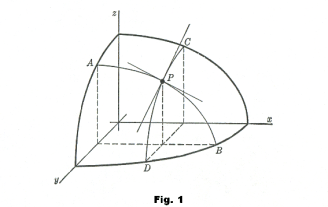
Geometric interpretation. The geometric interpretation of a partial derivative is the same as that for an ordinary derivative. It represents the slope of the tangent to that curve represented by the function at a particular point P. In the case of a function of two variables

z = f(x, y)

Fig. 1 shows the interpretation of ∂f/∂x and ∂f/∂y. ∂f/∂x corresponds to the slope of the tangent to the curve APB at point P (where curve APB is the intersection of the surface with a plane through P perpendicular to the y axis). Similarly, ∂f/∂y corresponds to the slope of the tangent to the curve CPD at point P (where curve CPD is the intersection of the surface with a plane through P perpendicular to the x axis).

Total differential. In the case of a function of a single variable the differential of the function y = f(x) is the quantity

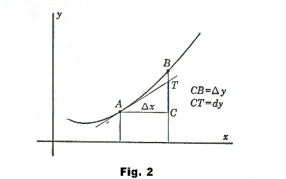
dy = f '(x) Δx .

This quantity is used to compute the approximate change in the value of f(x) due to a change Δx in x. As is shown in Fig. 2,

Δy = CB = f(x + Δx) - f(x)

while

dy = CT = f '(x)Δx .

When Δx is small the approximation is close. Line AT represents the tangent to the curve at point A.

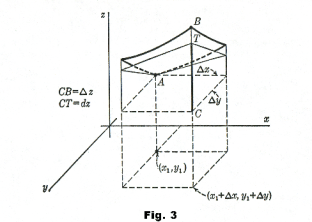
In the case of a function of two variables the situation is analogous. Let us start at point A(x₁, y₁, z₁) on the surface

z = f(x, y)

shown in Fig. 3 and let x and y change by small amounts Δx and Δy, respectively. The change produced in the value of the function z is

Δz = CB = f(x₁ + Δx, y₁ + Δy) - f(x₁, y₁) .

An approximation to Δz is given by

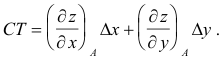
When Δx and Δy are small the approximation is close. Point T lies in that plane tangent to the surface at point A.

The quantity

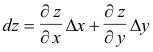
is called the total differential of the function z = f(x, y). Because is customary to denote increments Δx and Δy by dx and dy, the total differential of a function z = f(x, y) is defined as

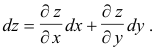
The total differential of three or more variables is defined similarly. For a function z = f(x, y, .. , u) the total differential is defined as

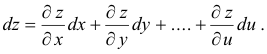
Each of the terms represents a partial differential. For example, the term

is the partial differential of z with respect to x. The total differential is the sum of the partial differentials.

Total derivative. Chain rule for functions of functions. If w = f(x, y, z, ...) is a continuous function of n variables x, y, z, ..., with continuous partial derivatives ∂w/∂x, ∂w/∂y, ∂w/∂z, ... and if x, y, z, ... are differentiable functions x = x(t), y = y(t) , z = z(t), etc. of a variable t, then the total derivative of w with respect to t is given by

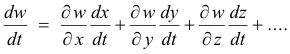
This rule is called the chain rule for the partial derivatives of functions of functions.

Similarly, if w = f(x, y, z, ...) is a continuous function of n variables x, y, z, ..., with continuous partial derivatives ∂w/∂x, ∂w/∂y, ∂w/∂z, ... and if x, y, z, ... are differentiable functions of m independent variables r, s, t ... , then

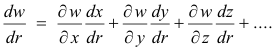
Note the similarity between total differentials and total derivatives. The total derivative 2) above can be obtained by dividing the total differential

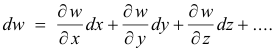
by dt.

As a special application of the chain rule let us consider the relation defined by the two equations

z = f(x, y); y = g(x)

Here, z is a function of x and y while y in turn is a function of x. Thus z is really a function of the single variable x. If we apply the chain rule we get

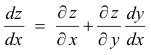
which is the total derivative of z with respect to x.

Def. Scalar point function. A scalar point function is a function that assigns a real number (i.e. a scalar) to each point of some region of space. If to each point (x, y, z) of a region R in space there is assigned a real number u = Φ(x, y, z), then Φ is called a scalar point function.

Examples. 1. The temperature distribution within some body at a particular point in time. 2. The density distribution within some fluid at a particular point in time.

Directional derivatives. Let Φ(x, y, z) be a scalar point function defined over some region R of space. The function Φ(x, y, z) could, for example, represent the temperature distribution within some body. At some specified point P(x, y, z) of R we wish to know the rate of change of Φ in a particular direction. The rate of change of a function Φ at a particular point P, in a specified direction, is called the directional derivative of Φ at P in that direction. We specify the direction by supplying the direction angles or direction cosines of a unit vector e pointing in the desired direction.

Theorem. The rate of change of a function Φ(x, y, z) in the direction of a vector with direction angles (α, β, γ) is given by

where s corresponds to distance in the metric of the coordinate system. That direction for which the rate of change at point P has its maximum value is called the gradient of Φ at P.

We shall prove the theorem shortly. First let us consider the same problem for two dimensional space.

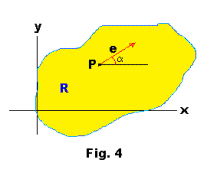
Let Φ(x, y) be a scalar point function defined over some region R of the plane. At some specified point P(x, y) of R we wish to know the rate of change of Φ in a particular direction. We specify the direction by supplying the angle α that a unit vector e pointing in the desired direction makes with the positive x direction. See Fig. 4. The rate of change of function Φ at point P in the direction of e corresponding to angle α is given by

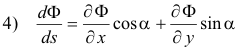
where s corresponds to distance in the metric of the coordinate system. We show this as follows:

Let

T = f(x, y)

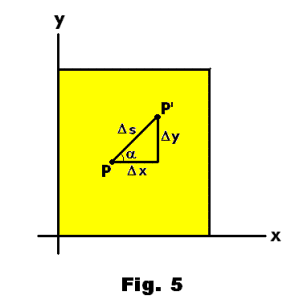
where T is the temperature at any point of the plate shown in Fig. 5. We wish to derive expression 4) above. In other words, we wish to derive the expression for the rate of change of T with respect to the distance moved in any selected direction. Suppose we move from point P to point P'. This represents a displacement Δx in the x-direction and Δy in the y-direction. The distance moved along the plate is

The direction is given by the angle α that PP' makes with the positive x-direction. The change in the value of T corresponding to the displacement from P to P' is

where ε is a quantity that approaches 0 when Δx and Δy approach 0.

If we divide ΔT by the distance moved along the plate, we have

From Fig. 5 we observe that Δx/Δs = cos α and Δy/Δs = sin α . Making these substitutions and letting P' approach P along line PP', we have

This is the directional derivative of T in the direction α.

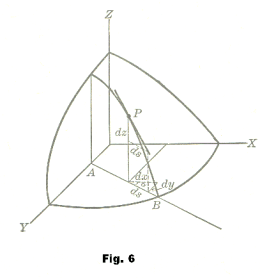
A geometric interpretation of a directional derivative in the case of a function z = f(x, y) is that of a tangent to the surface at point P as shown in Fig. 6.

Def. Directional derivative. The directional derivative of a scalar point function Φ(x, y, z) is the rate of change of the function Φ(x, y, z) at a particular point P(x, y, z) as measured in a specified direction.

Tech. Let Φ(x, y, z) be a scalar point function possessing first partial derivatives throughout some region R of space. Let P(x₀, y₀, z₀) be some point in R at which we wish to compute the directional derivative and let P'(x₁, y₁, z₁) be a neighboring point. Let the distance from P to P' be Δs. Then the directional derivative of Φ in the direction PP' is given by

where P' approaches P along the line PP' and Δs approaches 0.

Using this definition, let us now derive 3) above. In moving from P to P' the function Φ will change by an amount

where ε₁, ε₂, ε₃ are higher order infinitesimals which approach zero as P' approaches P i.e. as Δx, Δy and Δz approach zero. If we divide the change ΔΦ by the distance Δs we obtain a measure of the rate at which Φ changes as we move from P to P':

We now observe that Δx/Δs, Δy/Δs, Δz/Δs are the direction cosines of the line segment PP'. They are also the direction cosines of a unit vector e located at P pointing in the direction of P'. If the direction angles of e are α, β, γ, then Δx/Δs, Δy/Δs, Δz/Δs are equal to cos α, cos β, and cos γ, respectively. Thus 6) becomes

and

Let us note that 7) can be written in vector form as the following dot product:

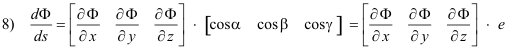
The vector

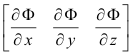
is called the gradient of Φ. Thus the directional derivative of Φ is equal to the dot product of the gradient of Φ and the vector e. In other words,

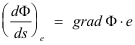
where

is the directional derivative of Φ in the direction of unit vector e.

If the vector e is pointed in the same direction as the gradient of Φ then the directional derivative of Φ is equal to the gradient of Φ.

Differentiation under the integral sign. Leibnitz’s rule. We now consider differentiation with respect to a parameter that occurs under an integral sign, or in the limits of integration, or in both places.

Theorem 1. Let

where a x b and f is assumed to be integrable on [a, b]. Then the function F(x) is continuous and Fʹ(x) = f(x) at each point where f(x) is continuous.

Integration with a parameter under the integral sign (Leibnitz’s rule). Let f(x, α) and ∂f/∂α be continuous in the region R:(a x b, c α d) of the x-α plane. Let

Then

Integration with a parameter under the integral sign and in the limits (Generalization of Leibnitz’s rule). Let

where u₁ and u₂ are functions of the parameter α i.e.

u₁ = u₁(α)

u₂ = u₂(α).

Let f(x, α) and ∂f/∂α be continuous in both x and α in the region R:(u₁ x u₂, c α d) of the x-α plane. Let u₁ and u₂ be continuous and have continuous derivatives for c α d. Then

where f(u₁, α) is the expression obtained by substituting the expression u₁(α) for x in f(x, α). Similarly for f(u₂, α). The quantities f(u₁, α) and f(u₂, α) correspond to ∂G/∂u₁ and ∂G/∂u₂ respectively and 12) represents the chain rule.

Order of differentiation. For most functions that one meets

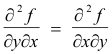
However, in some cases it is not true. Under what circumstances is it true? It is true if both functions f_yx and f_xy are continuous at the point where the partials are being taken.

Theorem. Let the function f(x, y) be defined in some neighborhood of the point (a, b). Let the partial derivatives f_x, f_y, f_xy, and f_yx also be defined in this neighborhood. Then if f_xy and f_yx are both continuous at (a, b), f_xy(a, b) = f_yx(a, b).

References

James & James. Mathematics Dictionary

Middlemiss. Differential and Integral Calculus

Spiegel. Advanced Calculus

Taylor. Advanced Calculus

Spiegel. Vector Analysis