Implicit functions, derivatives of implicit functions, Jacobian

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

IMPLICIT FUNCTIONS, DERIVATIVES OF IMPLICIT FUNCTIONS, JACOBIAN

Implicit functions. Let y be related to x by the equation

(1) f(x, y) = 0

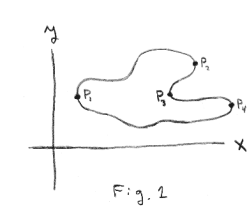
and suppose the locus is that shown in Figure 1. We cannot say that y is a function of x since at a particular value of x there is more than one value of y (because, in the figure, a line perpendicular to the x axis intersects the locus at more than one point) and a function is, by definition, single-valued. Although equation (1) above does not define y as a function of x, we can say that on certain judiciously chosen segments of the locus y can be considered to be a single-valued function of x [expressible as y = f(x)]. For example, the segment P₁P₂ could be separated out as defining a function y = f(x). As a consequence, it is customary to say that equation (1) defines y implicitly as a function of x; and we refer to y as an implicit function of x.

Def. Implicit function. A function defined by an equation of the form f(x, y) = 0 [in general, f(x₁, x₂, ... , x_n) = 0 ]. If y is thought of as the dependent variable, f(x, y) = 0 is said to define y as an implicit function of x.

James and James. Mathematics Dictionary.

Derivatives and implicit functions. Consider the locus of f(x, y) = 0 shown in Fig. 1. Let us ask the following question: “At a particular point on the locus what is the value of the quantity dy/dx?” This question can be answered at all points on the locus except points P₁, P₂, P₃ and P₄ (at these points the quantity dy/dx does not exist – it becomes infinite) and the answer is:

Proof

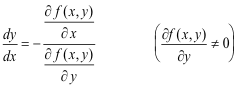
If we have an equation of the type f(x, y) = 0, and certain conditions are met, we can view one of the variables as a function of the other in the vicinity of a particular point (x₀, y₀) that satisfies the equation. The conditions that must be met are stated in the implicit function theorem.

Implicit-function theorem. A theorem stating conditions under which an equation, or a system of equations, can be solved for certain dependent variables. For a function of two variables, the implicit-function theorem states conditions under which an equation in two variables possesses a unique solution for one of the variables in a neighborhood of a point whose coordinates satisfy the equation. Tech. If F(x, y) and D_yF(x, y), the partial derivative of F(x, y) with respect to y, are continuous in the neighborhood of a point (x₀, y₀) and if F(x₀, y₀) = 0 and D_yF(x₀, y₀) ≠ 0, then there is a number ε > 0 such that there exists one and only one function f which is such that y₀ = f(x₀) and which is continuous and satisfies F[x, f(x)] = 0 for |x - x₀| < ε.

Example. x² + xy² + y - 1 and its partial derivative with respect to y, namely 2xy + 1, are both continuous in the neighborhood of (1, 0), and x² + xy² + y - 1 = 0 while 2xy + 1 ≠ 0 when x = 1, y = 0. Hence there exists a unique solution for y, in the neighborhood of (1, 0), which gives y = 0 for x = 1.

James and James. Mathematics Dictionary

Def. Jacobian of two or more functions in as many variables. For the n functions f_i(x₁, x₂, ... , x_n), i = 1,2, ... , n, the Jacobian is the determinant

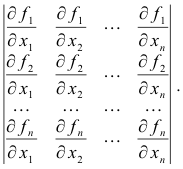
It is often denoted by

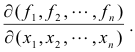
General implicit-function theorem. The general implicit-function theorem states conditions under which a system of n equations in n dependent variables and p independent variables possesses solutions for the dependent variables in the neighborhood of a point whose coordinates satisfy the given equations. Consider a system of n equations with the n + p variables

u₁, u₂, ..., u_n, and x₁, x₂, ... , x_p

namely

f₁(x₁, x₂, ... , x_p; u₁, u₂, ..., u_n) = 0

f₂(x₁, x₂, ... , x_p; u₁, u₂, ..., u_n) = 0

...........................................

f_n(x₁, x₂, ... , x_p; u₁, u₂, ..., u_n) = 0 .

Suppose that these equations are satisfied for the values x₁ = x₁⁰, ... , x_p = x_p⁰, u₁ = u₁⁰, ... , u_n = u_n⁰, that the functions f_i are continuous in the neighborhood of this set of values and possess first partial derivatives which are continuous for this set of values of the variables and, finally, that the Jacobian

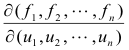
of these functions does not vanish for x₁ = x₁⁰, ... , x_p = x_p⁰, u₁ = u₁⁰, ... , u_n = u_n⁰. Under these conditions there exists one and only one system of continuous functions,

u₁ = Φ₁(x₁, x₂, ... , x_p)

u₂ = Φ₂(x₁, x₂, ... , x_p)

................................

u_n = Φ_n(x₁, x₂, ... , x_p)

defined in some neighborhood of

(x₁⁰, x₂⁰, ..... , x_p⁰),

which satisfy the above equations and which reduce to u₁⁰, u₂⁰, ..... , u_n⁰ for x₁ = x₁⁰, x₂ = x₂⁰... , x_p = x_p⁰.

James and James. Mathematics Dictionary

Differentiation of implicit functions. If we have an equation such as f(x, y, ... , u) = 0 which defines a variable as a function of others implicitly, there are two techniques for computing derivatives.

1. Direct differentiation. Given a particular variable to be considered as the dependent variable, if it is possible to solve the equation for the dependent variable in terms of the independent variables, we can compute the derivative directly by formula.

Example. Compute dy/dx for the equation y - 3x² + 5x + 1 = 0 . Solution. Solve the equation for y to get

y = 3x² -5x -1

and compute the derivative directly as dy/dx = 6x - 5.

2. Implicit differentiation. Decide which variable is to be considered the dependent variable and which the independent. Say y is to be considered the dependent variable in f(x, y) = 0. Regarding y as the dependent variable, differentiate the equation as it stands with respect to the independent variable x and then solve the resulting relation for dy/dx. This method is known as implicit differentiation.

Example. Compute dy/dx for the equation x⁵ + x²y³ - y⁶ + 7 = 0 .

Solution. Differentiating implicitly, we get

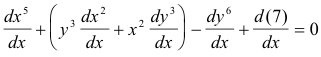
Solving this for dy/dx gives

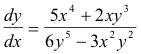
Because in most cases it is difficult or impossible to solve for the dependent variable, we usually use the method of implicit differentiation.

Theorem. In the equation f(x, y) = 0 which defines y as a function of x implicitly, the derivative dy/dx is given in terms of the partial derivatives of f(x, y) by

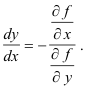
Proof. The total differential of the function z = f(x, y) is given by

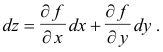
If we make the constraint that z = f(x, y) = 0 (i.e. the values of x and y are restricted to the solution set of f(x, y) = 0), then z is constant, dz is zero, and the total differential becomes

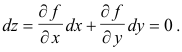
So, solving for dy/dx, we get

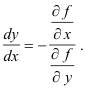
Partial derivatives of implicit functions. Let two or more variables be related by an equation of type

F(x, y, z, ...) = 0 .

Providing the conditions of the implicit-function theorem are met, we can take one of the variables and view it as a function of the rest of the variables. If we pick z as the dependent variable, the partial derivatives of z with respect to the other variables are given by

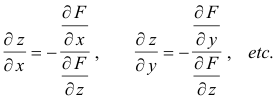
Proof. Th proof is essentially the same as the proof above for the case f(x, y) = 0 since all variables except the two in question are treated as constants when taking the partials..

Systems of equations.

Problem. Given the system of equations

F(u, v, w, x, y) = 0

G(u, v, w, x, y) = 0

H(u, v, w, x, y) = 0

find

considering x and y as independent variables and u, v, w as dependent variables.

Solution. If the conditions given by the implicit-function theorem are met we can view three of the variables, such as u, v and w, as defined implicitly as functions of the other two variables, in the vicinity of a particular point (u₀, v₀, w₀, x₀, y₀) that satisfies the equations. From 3 equations in 5 variables, we can (theoretically at least) determine 3 variables in terms of the other 2. Thus 3 variables are dependent and 2 are independent. The total differentials of the functions F, G and H are given by

dF = F_udu + F_vdv + F_wdw + F_xdx + F_ydy = 0

dG = G_udu + G_vdv + G_wdw + G_xdx + G_ydy = 0

dH = H_udu + H_vdv + H_wdw + H_xdx + H_ydy = 0 .

Dividing these three equations through by dy, and remembering that x is held constant, we obtain the following system of equations that must be satisfied:

F_uu_y,+ F_vv_y + F_ww_y + F_y = 0

G_uu_y,+ G_vv_y + G_ww_y + G_y = 0

H_uu_y,+ H_vv_y + H_ww_y + H_y = 0

where F_u represents the partial derivative of F with respect to u, u_y, represents the partial derivative of u with respect to y, etc. Solving this system by Cramer’s rule we get

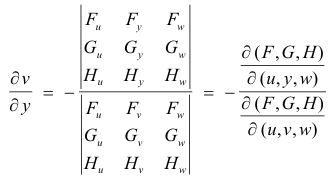
If instead of v_y we wanted u_y, it would be given by

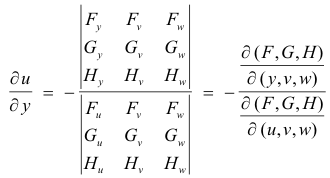
These results apply to any number of equations or variables.

References.

James and James. Mathematics Dictionary.

Oakley. The Calculus (COS).

Spiegel. Advanced Calculus.