Geodesics, geodesic curvature, geodesic parallels, geodesic coordinates, geodesic torsion, Gauss-Bonnet theorem

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

GEODESICS, GEODESIC CURVATURE, GEODESIC PARALLELS, GEODESIC COORDINATES, GEODESIC TORSION, GAUSS-BONNET THEOREM

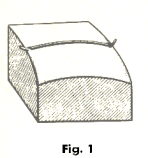
Geodesic. Intuitively, a geodesic is the shortest arc between two points on a surface. If we stretch a rubber band between two points on a convex surface, the rubber band will take the path of the geodesic. See Fig. 1. A geodesic C on a surface S has the properties that at each point of C the principal normal coincides with the normal to S and the geodesic curvature vanishes identically. Conversely, if on a curve C on a surface S, the principal normal coincides with the surface normal at every point, or if the geodesic curvature vanishes identically at every point, the curve is a geodesic. If a straight line lies on a surface, then the line is a geodesic of the surface.

Although defining a geodesic as the shortest arc between two points on a surface gives the main idea of a geodesic, there is a problem with it as a definition. Not every geodesic is a shortest path in the large, as can be seen by noting that on the surface of a sphere every arc of a great circle is a geodesic even though an arc will be the shortest path between two points only if that arc is not greater than a semicircle. From this example we see that a geodesic can be a closed curve. Because of this difficulty a geodesic is often defined as an arc C on a surface S at each point of which the principal normal coincides with the normal to S — or an arc at every point of which the geodesic curvature vanishes identically.

Theorem 1. If two surfaces are tangent along a curve that is a geodesic on one of them, then this curve will be a geodesic on the other.

Reason? At each point along the curve the principal normals coincide with the surface normals.

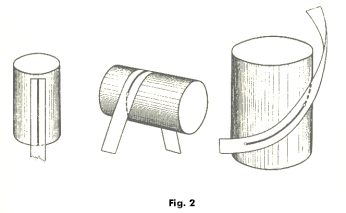
For an illustration of this theorem see Fig. 2. A straight plane strip of paper with a median line drawn on it is placed in different positions on a cylinder. One can see from this example that a geodesic line on a cylinder can be one of three things: a straight line, a circle or a helix.

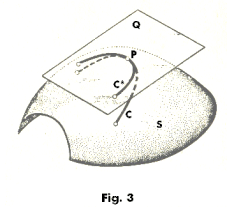
Geodesic curvature. Let C be a curve on a surface S. The geodesic curvature of C at a given point P is defined as the curvature, at P, of the orthogonal projection of C onto the plane Q tangent to S at point P. See Fig. 3, where C* is the projection of C onto the tangent plane Q. The geodesic curvature of C at P is defined then as the curvature of C* at P.

For the motivation that led to this definition let us note that if C represents an arc of minimum length between two points A and B on a surface S and point P lies on the arc then the projection of C onto the tangent plane at point P should be a straight line and the geodesic curvature of C in that situation should be counted as zero. Thus as candidates for the arcs of minimum length we are led to consider those curves where the curvature of the orthogonal projection of the curve onto the tangent plane is zero.

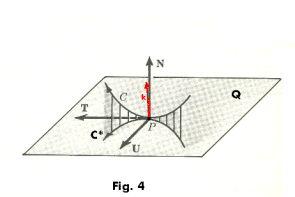
Formula for computing geodesic curvature. Given a curve C: u = u(s), v = v(s) on a surface S: where s is arc length. The curvature vector of C at point P is defined as the vector k =dt/ds where t is the tangent vector t = . Let N be the unit surface normal at point P, T be the unit tangent vector to C at point P and U be a unit vector in the tangent plane Q defined by U = N T creating the orthonormal triad shown in Fig. 4. Vector k is orthogonal to T, lying in the N-U plane. Then the geodesic curvature vector k_g is the component of k along vector U i.e.

k_g = (k•U)U

Theorem 2. The geodesic curvature vector k_g of a curve C at P is the vector projection of the curvature vector k of C at P onto the tangent plane at P.

One can write the vector k as

k = k_g + k_n

where k_g is the component of k along the U axis and k_n is its component along the N axis. The component k_n along the N axis is the normal curvature of the surface S at P in the direction of tangent T i.e. the curvature of the normal section defined by N and T.

Let the magnitude of the vector k_g be denoted by k_g i.e. k_g = |k_g| . Then

k_g = k_gU .

The scalar k_g is called the geodesic curvature of C at P.

Let us denote the magnitude of the vector k by k, i.e. k = |k|. Then the curvature k of curve C at point P is related to the geodesic curvature k_g at P by

k_g = k cos θ

where θ is the angle between the osculating plane of C and the tangent plane Q.

Theorem 3. If point P on curve C of surface S is represented by the position vector then k_g is given by the following box products

k_g = [T k N]

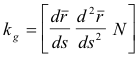
where N is the normal to the surface at P and T is the unit tangent to C at P.

This theorem follows from k_g = k∙U = k∙(N T).

Liouville’s formula for geodesic curvature. Given: The curves C₁ and C₂ of an orthogonal system on a surface are so directed that at each point the directed angle from the directed curve C₁ to the directed curve C₂ is π/2 (e.g. curves C₁ and C₂ could be u- and v-coordinate curves of an orthogonal system). Then the geodesic curvature of an arbitrary directed curve C: u = u(s), v = v(s) is then given by the formula

k_g = k₁ cos θ + k₂ sin θ + dθ/ds

where θ is the directed angle at an arbitrary point P of C from the directed curve C₁ through P to the directed curve C, k₁ is the geodesic curvature of curve C₁, k₂ is the geodesic curvature of curve C₂, and s is arc length.

Geodesics and asymptotic lines. A curve is an asymptotic line if and only if at each point of the curve k_n = 0; a curve is a geodesic if and only if at each point of the curve k_g = 0. A asymptotic line is either a straight line or a curve along which the osculating plane and the tangent plane coincide; a geodesic is either a straight line or a curve along which the osculating plane is perpendicular to the tangent plane.

Theorem 4. The geodesic curvature k_g of a curve is equal numerically to the ordinary curvature k at every point of the curve if and only if the curve is an asymptotic line.

The geodesic curvature k_g of a curve which is not a straight line is equal numerically to the ordinary curvature k at every point of the curve if and only if the osculating plane of the curve at each point is the tangent plane to the surface at the point. As an example consider a circle in a plane, which meets the requirements for being an asymptotic line whose osculating plane at each point is the tangent plane.

Beltrami’s formula for geodesic curvature. Given a curve C: u = u(s), v = v(s) on a surface S: where s is arc length. Beltrami’s formula for the geodesic curvature at point P of the curve is:

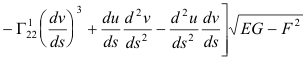
where the Γ_ij^k are the Christoffel symbols of the second kind.

Derivation.

In contrast to k_n which depends on both the first and second fundamental coefficients, the geodesic curvature k_g depends only on the first fundamental coefficients E, F and G (and their derivatives) and is thus an intrinsic property of the surface. This is evident in the above formula since the functions Γ_ij^k are functions of the first fundamental coefficients E, F and G only.

Geodesic curvature of the coordinate curves. We can compute the values of du/ds and dv/ds in 1) above for the u- and v-coordinate curves from the first fundamental quadratic form. For the u-coordinate curves where v = constant, dv/ds = 0 and du/ds = 1/ . Along the v-coordinate curves where u = constant, du/ds = 0 and dv/ds = 1/ . Substituting into 1) we get

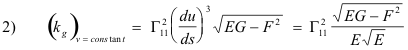
For the case where the coordinate curves are orthogonal, F = 0, Γ₁₁² = -½E_v/G, Γ₂₂¹ = -½G_u/E. Thus

Theorem 5. The u-curves on a surface are geodesics if and only if Γ₁₁² = 0; and the v-curves if and only if Γ₂₂¹ = 0.

Proof. This theorem follows directly from 2) above.

Theorem 6. If the coordinate curves form an orthogonal system, the u-curves are geodesics when and only when E is a function of u alone, and the v-curves are geodesics when and only when G is a function of v alone.

Proof. This theorem follows directly from 3) above. For the u-curves, if E is a function of u alone, then E_v = 0 and k_g = 0. For the v-curves, if G is a function of v alone, then G_u = 0 and k_g = 0.

Corollary. If both the u-curves and the v-curves are geodesics then E and G are, respectively, functions U(u) and V(v), of u and v.

Theorem 7. If there exists on a surface an orthogonal system of geodesics, the system is a developable or a plane.

Examples of systems of orthogonal geodesics.

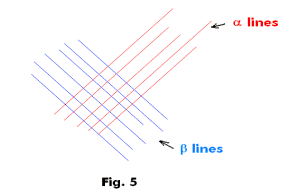
1. Let α be the set of all lines in the plane directed in any specified direction. Let β be the set of all lines in the plane perpendicular to the α lines. See Fig. 5. Then the two families of lines constitute an orthogonal system of geodesics.

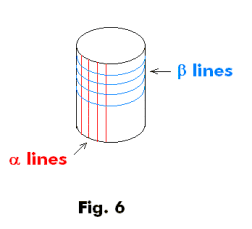
2. Let α be the set of all lines in the surface of a cylinder parallel to the axis of revolution. Let β be the set of all circles formed as plane sections by planes cutting through the cylinder perpendicular to the axis of revolution. See Fig. 6. Then the two families of lines constitute an orthogonal system of geodesics.

Differential equations of the geodesics.

Theorem 8. Let S be a simple surface element defined by the one-to-one mapping

x = x(u, v)

y = y(u, v)

z = z(u, v)

of a region R of the uv-plane into xyz-space. Then a directed curve C on S represented parametrically in terms of arc length s by

u = u(s)

v = v(s)

is a geodesic if and only if u(s) and v(s) satisfy the following differential equations:

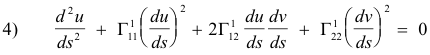
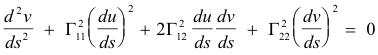
Using equations 4) and an existence theorem from the theory of differential equations one can prove the following:

Theorem 9. In the neighborhood of a point P on a surface of class 3 there exists one and only one geodesic through P in any given direction.

Theorem 10. Let S: be a simple surface element of class 2 such that E = E(u), F = 0, and G = G(u). Then

1. The v-curves are geodesics.

2. The u-curve v = v₀ is a geodesic if and only if G_u(u₀) = 0.

3. A curve of the form is a geodesic if and only if

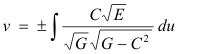
where C is a constant.

*************************************************

Geodesic parallels, geodesic coordinates

*************************************************

Def. Trajectory. A curve which cuts all curves (or surfaces) of a given family at the same angle. An orthogonal trajectory is a curve which cuts all the members of a given family of curves (or surfaces) at right angles.

James/James. Mathematics Dictionary.

Geodesic parallels. The orthogonal trajectories of a family of lines in the plane have the following property: the segments cut from the lines by any two of them are all equal. The orthogonal trajectories of a family of geodesics on an arbitrary surface have the same property. Any two of them cut equal segments from the geodesics. Conversely, if any two orthogonal trajectories of a family of curves on a surface cut equal segments from the curves of the family, the curves of the family are geodesics on the surface.

Theorem 11. A necessary and sufficient condition that the segments cut from the curves of a family of curves on a surface by two arbitrarily chosen orthogonal trajectories of the family be all equal is that the curves of the family be geodesics on the surface.

Def. Geodesic parallels. The orthogonal trajectories of a family of geodesics are known as geodesic parallels. They are called parallels because each two of them are equally distant and, geodesic parallels because the distances in question are measured along geodesics.

Example of geodesic parallels. An example of geodesic parallels are the parallel circles that are traced out on a surface of revolution by the individual points of the plane curve that is rotated to generate the surface. The parallels of latitude on a sphere are geodesic parallels.

By Theorem 7, a family of geodesic parallels can consist of geodesics only if the surface is a developable or a plane. Normally geodesic parallels are not geodesics.

Geodesic parallels on a surface. Given a smooth curve C₀ on a surface S, there exists a unique family of geodesics on S intersecting C₀ orthogonally. If segments of equal length s be measured along the geodesics from C₀, then the locus of their end points is an orthogonal trajectory C_s of the geodesics. The curves C_s are geodesic parallels.

James/James. Mathematics Dictionary.

Geodesic coordinates. A simple surface element where the coordinate curves are orthogonal and one of the families of coordinate curves are geodesics is called a set of geodesic coordinates.

Def. Geodesic parameters (coordinates). Parameters u, v for a surface S such that the curves u = const. are the members of a family of geodesic parallels, while the curves v = const. = v₀ are members of the corresponding orthogonal family of geodesics, of length u₂ - u₁ between the points (u₁, v₀) and (u₂, v₀). A necessary and sufficient condition that u, v be geodesic parameters is that the first fundamental form of S reduce to ds² = du² + G dv².

James/James. Mathematics Dictionary.

From Theorem 6 we know that a necessary and sufficient condition for the u-curves to be geodesics and the v-curves to be geodesic parallels orthogonal to them is that E = U(u) and F = 0. This means that the first fundamental form has the form

5) ds² = U(u)du² + Gdv².

If we then make a substitution

5) becomes

Geodesic polar coordinates. These are geodesic parameters u, v for a surface S, except that the curves u = const. = u₀, instead of being geodesic parallels, are concentric geodesic circles, of radius u₀, and center, or pole, P corresponding to u = 0; the curves v = v₀ are the geodesic radii; and for each v₀, v₀ is the angle at P between the tangents to v = 0 and v = v₀. Necessary and sufficient conditions that u, v be geodesic polar coordinates are that the first fundamental quadratic form of S reduce to ds² = du₂ + μ²dv², η 0, and that at u = 0 we have η = 0 and =1. All points on u = 0 are singular points corresponding to P.

James/James. Mathematics Dictionary.

Geodesic circle on a surface. If equal lengths are laid off from a point P of a surface S along the geodesics through P on S, the locus of the end points is an orthogonal trajectory of the geodesics. The locus of end points is called a geodesic circle with center at P and radius r. The “radius” r is a geodesic radius; it is the geodesic distance on the surface from the “center” P to the circle. See “geodesic polar coordinates”.

James/James. Mathematics Dictionary.

Bonnet’s formula for geodesic curvature. Let a curve C on a surface S: be defined by an equation of the form

Then Bonnet’s formula for the geodesic curvature at point P of the curve is:

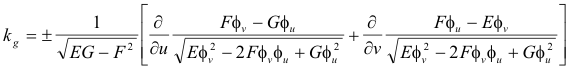
where E, F, G, L, M, N are the first and second fundamental coefficients.

Geodesic torsion.

Torsion of a geodesic. The torsion of a geodesic passing through point P of a surface in the direction of the unit tangent vector T is given by

where is the unit surface normal at point P and is the position vector at point P, or, equivalently, by

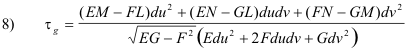
where E, F, G, L, M, N are the first and second fundamental coefficients.

Derivation

We note that the condition that the geodesic torsion τ_g = 0 along a curve is tantamount to the condition that the curve is a line of curvature. A curve is a line of curvature if and only if at each point on the curve the direction of its tangent satisfies

9) (EM - FL)du² + (EN - GL)dudv + (FN - GM)dv² = 0 .

The left member of 9) is identical to the numerator in 8) so if τ_g = 0 along a curve the curve is a line of curvature.

Theorem 12. The geodesic torsion of a curve is identically zero if and only if the curve is a line of curvature.

Theorem 13. A geodesic, which is not a straight line, is a plane curve if and only if it is a line of curvature.

Def. Geodesic torsion of a surface at a point in a given direction . The expression for τ_g in 7) above is similar to the expression for normal curvature in that it depends only on the point P and on the direction dv/du at P. The quantity τ_g defined by 7) is called the geodesic torsion of the surface at P in the direction dv/du. Though the torsion at P of the geodesic which issues from P in a given direction fails to exist when the geodesic is a straight line, the geodesic torsion always exists because 7) defines it for every direction at P, regardless of the nature of the geodesic in the direction.

Theorem 14. The geodesic torsion at a point P on a surface is related to the normal curvatures k₁ and k₂ at P by

10) τ_g = ½ (k₂ - k₁) sin 2θ

where θ is the angle, in the tangent plane, measured counterclockwise from the direction of minimum curvature k₁ .

At an umbilic, the geodesic torsion is zero in every direction. If we exclude this case, 9) reveals that the geodesic torsion is zero in the two principal directions and takes on its extreme values in the two perpendicular directions that bisect the angles between the principal directions.

Since sin 2(θ + π/2) = - sin 2θ and sin 2(-θ) = - sin 2θ we have the following:

Theorem 15. 1. The geodesic torsions in two perpendicular directions, θ and θ + π/2, are negatives of each another. 2. The geodesic torsions in two directions +β and -β, as measured from a principal direction, are negatives of each other.

In particular, the two extreme values of the geodesic torsion at a point are negatives of each another. Also, the geodesic torsions in the two asymptotic directions are negatives of one another.

Def. Geodesic torsion of a curve on a surface. By the geodesic torsion of a curve C (whether curve C is a geodesic or not) at a point P is meant the geodesic torsion of the surface at P in the direction which C has at P. Thus all curves through P that have the same direction at P have the same geodesic torsion at P.

Theorem 16. The relationship between the geodesic torsion τ_g of a curve C : u = u(s), v = v(s) at a point P on a surface S and the ordinary torsion τ of C at point P is given by

11) τ_g = dα/ds - τ

where α is the directed angle from the unit surface normal N to the principal normal n to C.

We note that the angle α represents the angle between the osculating plane of C and the tangent plane to the surface.

Theorem 17. The ordinary torsion and the geodesic torsion of a curve C, which is not a straight line, are identically equal if and only if the osculating plane of C makes a constant angle with the tangent plane to the surface.

It follows from 11) that if τ_g = 0, then τ = 0 when and only when dα/ds = 0. In other words:

Theorem 18. A necessary and sufficient condition that a line of curvature, other than a straight line, be a plane curve is that its osculating plane always makes the same angle with the tangent plane to the surface.

The Gauss-Bonnet Theorem, published by Bonnet in 1848, is an application of Green’s theorem to the integral of geodesic curvature.

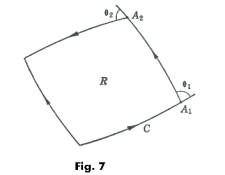
Gauss-Bonnet Theorem. If the Gaussian curvature K of a surface is continuous in a simply connected region R bounded by a closed curve C composed of k smooth arcs making at the vertices exterior angles θ₁, θ₂, ... ,θ_k, then

where k_g represents the geodesic curvature of the arcs. See Fig. 7.

References.

1. Mathematics, Its Contents, Methods and Meaning. Vol. II, Chapter VII.

2. Graustein. Differential Geometry.

3. Lipschutz. Differential Geometry. Chapter 11.

4. James/James. Mathematics Dictionary.

5. Struik. Lectures on Classical Differential Geometry.