Motions of space. Intuitive meaning of the concept of a conjugate transformation of a transformation A

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Motions of space. Intuitive meaning of the concept of a conjugate transformation B^-1AB of a transformation A

Motions of space. The possible motions of space (three dimensional space) are classified as proper motions (or motions of the first kind) and improper motions (or motions of the second kind).

Proper motions (motions of the first kind) are translations, rotations, and spiral motions. Improper motions (motions of the second kind) are all other motions, including reflections.

In a plane the proper motions are translations and rotations. The improper motions are all other motions including reflections.

Let us note that the set of all possible translations in the plane meet the axiomatic requirements for a group. Collectively they form a group. The same can be said for the set of all possible rotations.

Conjugate transformations. The transformation B^-1AB is said to be obtained from A by transforming A by B. The element C = B^-1AB is said to be conjugate to A by means of B.

What is the intuitive meaning of the transformation B^-1AB? The answer lies in the following theorem:

Theorem 1. If the image of m is n under transformation A (i.e. mA = n) then the image of mB is nB under the transformation C = B^-1AB. That is, if mA = n, then mBC = nB, or equivalently,

mB(B^-1AB) = nB

Proof. (mB)B^-1AB = m(BB^-1)AB = mAB = nB

Note here that C is a conjugate of A by means of B. In general, the transform x^-1ax decomposes the members of a group into k disjoint equivalence classes where members of the same class are said to be conjugate to each other. What is the common property that distinguishes the members of a particular equivalence class? What property is it that makes members of a particular conjugate class conjugate to each other?

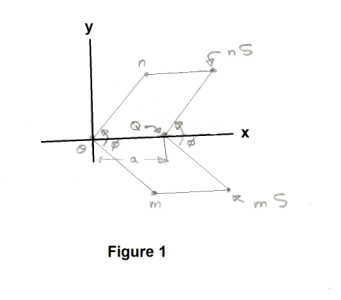
1. Intuitive meaning of the concept of a conjugate transformation B^-1AB of a transformation A for motions of the plane. There are two motions of the plane: translation and rotation. Let R represent a rotation of the plane around the origin O through the angle φ. Let S be a translation of the plane by an amount a in the positive x direction and let Q be the point into which the origin O is carried by the translation. See Figure 1. Let C = S^-1RS be the conjugate of R by means of S. We wish to show that if the image of m is n under transformation R (rotation) about origin O (i.e. mR = n) then the point mS is carried into nS by the transformation C = S^-1RS. In other words, we wish to show that if mR = n, then (mS)C = nS. That it does is obvious from

1) (mS)C = (mS)(S^-1RS) = (mR)S = nS

since (mS)S^-1 = m and (mR) = n. Each of these operations can be followed, a step at a time, from Fig. 1. We can see that the transformation C = S^-1RS represents a rotation about the point Q by the same angle φ as the transformation R. Following 1) a step at a time, we see that S^-1 carries mS into m, R carries m into n, and S carries n into nS. Thus S^-1RS carries mS into nS.

Transforms of the motions of the plane

The transform of an element a of a group G by an element x is the element b = x^-1ax. The element b is said to be conjugate to a by means of x.

Transform of a rotation by a translation. Let R_O be a rotation of a plane around a point O through the angle φ. Let S be a translation of the plane. Then the transform C = S^-1 R_OS of rotation R_O by translation S is a rotation of the plane around another point Oʹ in the plane by that same angle φ, where Oʹis the point into which O is carried by the translation S.

Transform of a translation by a rotation. If a translation of the plane characterized by the vector A is transformed by means of a rotation R_O by the angle φ, we obtain again a translation of the plane, characterized by a different vector B.

Transform of a translation by a translation. The transform of a translation by a translation is a translation.

Transform of a rotation by a rotation. The transform of a rotation by a rotation is a rotation.

Thus the conjugate of a rotation by means of a translation is a rotation; the conjugate of a translation by means of a rotation is a translation; the conjugate of a translation by means of a translation is a translation; the conjugate of a rotation by means of a rotation is a rotation.

2. Intuitive meaning of the concept of a conjugate transformation B^-1AB of a transformation A for the case of permutation groups. Just what is the intuitive meaning of the transformation C = B^-1AB when A and B represent elements of permutation groups?

Some notation and conventions. We will denote transformations of a finite set M = {m₁, m₂, ... , m_n} into itself, transformations such as

by capital letters such as A, B, C, etc. In addition, we will denote the image of an arbitrary element m in M by the notation mA. For example, if

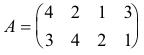
then 4A = 3, 2A = 4, 1A = 2, 3A = 1.

Let

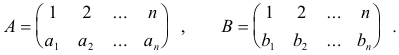
then

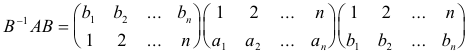
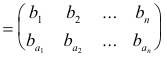
where

represent the images of a₁, a_{2, ... ,}a_n respectively under the transformation B i.e.

If we examine the matrix

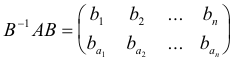
we note that the upper row is obtained by subjecting all the elements in the upper row of A to the transformation specified by B and that the lower row is obtained by subjecting all the elements in the lower row of A to the transformation specified by B (in other words, the upper and lower rows of B^-1AB are the images of the upper and lower rows of A under the transformation B).

Example. Let

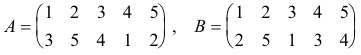
then

Let us now ask a question: How does the above result relate to Theorem 1? Well, the m of Theorem 1 corresponds to the upper row of A and the n of Theorem 1 corresponds to the lower row of A. Transformation

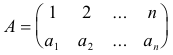
is viewed as transforming the ordered set (1, 2, ... , n) into the ordered set (a₁, a_{2, ... ,}a_n). The upper row of B^-1AB then consists of the image of m under B and the lower row consists of the image of n under B. Thus the transformation B^-1AB does then constitute a transformation that carries mB into nB. So the above result does follow directly from Theorem 1.

In the case where permutations A and B are expressed in cyclic notation the above result can be expressed as follows:

Theorem 2. Let A be a cyclic permutation A = (a₁, a_{2, ... ,}a_n). Then the conjugate transformation C = B^-1AB is given by C = (a₁B, a₂B, ... , a_nB).

In other words, the cyclic representation of C = B^-1AB is obtained from the cyclic representation of A by replacing each element in the cyclic representation of A by its image under B.

A direct consequence of Theorem 2 is the following corollary:

Corollary. The conjugate of any cycle in a permutation group is another cycle of the same length.

References

Mathematics, Its Content, Methods and Meaning. Vol. 3