Conjugates, conjugate classes, automorphisms, normal subgroups, quotient groups, homomorphic mapping of groups

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

CONJUGATES, CONJUGATE CLASSES, AUTOMORPHISMS, NORMAL SUBGROUPS, QUOTIENT GROUPS, HOMOMORPHIC MAPPING OF GROUPS

Def. Transform. transform of an element of a group. Given group G. The transform T_x(a) of an element a ∈ G by an element x ∈ G is the element a' = x ^-1ax. The transform is a function or mapping that maps an element a ∈ G into an element a' = x ^-1ax ∈ G.

Conjugates of elements in a group. Given group G. The transform a' = x ^-1ax of an element a ∈ G by an element x ∈ G is called the conjugate of a. Here a' is said to be the conjugate of a under “conjugation” by x or by means of x.

Condition for two elements of a group to be conjugate. Given group G. The element a ∈ G is conjugate to an element b ∈ G if there exists an element x ∈ G such that a = x ^-1bx.

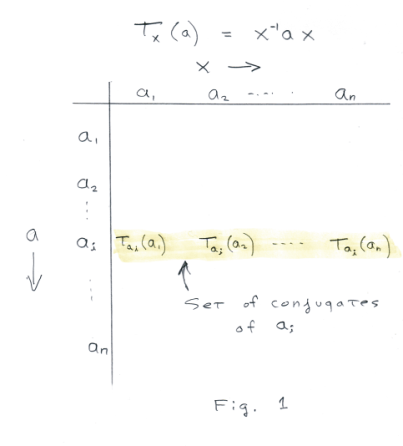
Computing all elements conjugate to a particular element. Let G = {a₁, a₂, ... , a_n} be a group containing n elements. The set of all transforms of an element a_i ∈G by all elements a_i (i = 1, n) of G is the set of all conjugates of a_i in G and constitutes a conjugate set (or class) in G. This set will contain the element a_i itself since an element is conjugate to itself. To compute all the elements of each conjugate class we compute the table of Fig. 1. In the figure the highlighted line contains the conjugates of element a_i.

Conjugate classes. The relationship of conjugacy is a an equivalence relation defined on the elements of G:

1) Every element of a group is conjugate to itself (since a = a^-1aa).

2) If a is conjugate to b then b is conjugate to a (because if b = x^-1ax then xbx^-1 = a or

a = (x^-1)^-1bx^-1).

3) If a is conjugate to b and b is conjugate to c then a is conjugate to c ( because if b = x^-1ax and c = y^-1by , then c = y^-1x^-1axy = (xy)^-1a(xy) ).

Thus conjugacy is a relation that is reflective, symmetric and transitive, making it an equivalence relation that splits a group up into disjoint equivalence classes of conjugate elements.

Def. Automorphism. An automorphism of a group G is a one-to-one mapping f :G → G (i.e. a one-to-one correspondence between elements of G) where f(ab) = f(a)f(b) for all a,b in G. It represents an isomorphism of group G with itself.

Theorem. For any fixed element x of a group G, the mapping T_x(a) : a → x ^-1ax carrying a into x ^-1ax effects an automorphism on G. Each x ∈ G gives a different automorphism.

Thus this theorem says that the mapping T_x(a) : a → x ^-1ax establishes a correspondence between members of G in which, for any selected x ∈ G, f(ab) = f(a)f(b) for all a,b in G.

Proof. We need to prove that for any x in G, f(ab) = f(a)f(b) for all a,b in G. Thus we need to prove x^-1(ab)x = (x^-1ax)(x^-1bx) for all a,b in G. The proof follows immediately since (x^-1ax)(x^-1bx) = x^-1a(xx^-1)bx = x^-1abx.

Let H = {h₁, h₂, .... ,h_n} be a subgroup of G. For a fixed x ∈ G, apply the transform T_x(a) : a → x ^-1ax to all elements h₁, h₂, .... ,h_n of H mapping them into elements k₁, k₂, .... ,k_n. in G. The elements k₁, k₂, .... ,k_n then correspond to a subgroup K of G that is isomorphic to H. Each element k_i ∈ K is a conjugate of its counterpart h_i ∈ H. Group K is said to be conjugate to H. Thus, in general, the transform T_x(a) : a → x ^-1ax effects a automorphic mapping from one subgroup of G into another subgroup of G. Each x_i ∈ G gives a different automorphic mapping of group H, mapping H into another (or perhaps the same) subgroup of G. The set of all subgroups into which the transform T_x(a) : a →x ^-1ax maps H for all the different x_i ∈ G is a set of subgroups conjugate to H. Any two of the subgroups are conjugate to each other.

Note. Understanding of conjugate classes and automorphisms is aided considerably by studying The Dihedral Group of the Square .

Conjugate set of subgroups. Given group G and subgroup H. The set of different subgroups obtained by transforming a given subgroup H by all the elements of the group G is a conjugate set of subgroups; any two of these subgroups are conjugate to each other.

Inner and outer automorphisms.. Automorphisms T_x(a) : a → x ^-1ax on a group generated by the elements x are called inner automorphisms. All other automorphisms on a group are called outer automorphisms.

Note. If group G has n elements there will be n inner automorphisms T_x(a) : a → x ^-1ax , one for each element x_i ∈ G (although some may be identical).

Self-conjugacy of elements. If the inner automorphism T_x(a) : a → x ^-1ax maps a into itself for all x ∈ G , i.e. if a is sent into itself for every inner automorphism of G, a is called self-conjugate. The element a ∈ G is self-conjugate if and only if x ^-1ax = a or ax = xa for all x ∈ G, that is, if and only if a commutes with every element of G.

Conjugacy of complexes. The complex H of a group G is conjugate to the complex K of G if there exists an element x ∈ G such that H = x ^-1Kx.

Thus, given a subgroup K, any subgroup H given by H = x ^-1Kx , for any x ∈ G, is conjugate to K.

Theorem. All conjugates of a subgroup G are subgroups of G.

Self-conjugacy of complexes. The complex H is self-conjugate if x ^-1Hx = H for all x ∈ G, that is, if the subset H is mapped into itself by every inner automorphism of G.

************************************

Theorems.

1] An inner automorphism T_x(a) : a → x ^-1ax transforms a subgroup H into a subgroup x ^-1Hx, which is said to be a conjugate of H or conjugate to H.

2] If a subgroup H is identical with all its conjugate subgroups, i.e.

x ^-1Hx = H for every x,

it simply means that the subgroup H commutes with every element x i.e.

xH = Hx for every x,

and is, therefore, a normal divisor (or normal subgroup).

In other words, the subgroups invariant under all inner automorphisms are the normal divisors.

3] A subgroup is a normal divisor (or normal subgroup) if it contains with any element a all its conjugate elements x ^-1ax as well.

4] A subgroup H is a normal subgroup of G if and only if H is self-conjugate i.e. if x ^-1Hx = H for all x ∈ G (i.e. if H contains the conjugates of all its elements).

5] If H is a normal subgroup of a group G, then HK = KH for every complex K of G.

6] If H is a normal subgroup of G and K is any subgroup of G, then HK = KH is a subgroup of G.

7] A subgroup H is normal if and only if all its right cosets are equal to its left cosets.

**********************

Quotient groups. The cosets of a normal subgroup H of a group G form a group under the operation of complex multiplication. This group formed by the cosets is called the quotient group of G by H and is denoted by G/H. The unit element of G/H is H and the inverse of a coset aH is the coset a ^-1H.

Homomorphic mappings of groups. The following theorem is fundamental to the entire theory of homomorphic mappings:

Theorem. Under homomorphic mapping of an arbitrary group G onto a group G', the set N of elements of G that are mapped into the identity element e' of G' is a normal subgroup of G; the set of elements of G that are mapped into an arbitrary fixed element of G' is a coset of G with respect to N, and the one-to-one correspondence thus established between the cosets of G with respect to N and the elements of G' is an isomorphism between G' and the quotient group G/N.

Proof. Let a, b be arbitrary elements of N. This means that a' = b' = c' where, as before, the prime denotes the images of elements of G in H. But then

(ab)' = a'b' = e'e' = e'

(a^-1)' = a'^-1 = e'^-1 = e' ;

i.e., ab and the inverse elements a^-1, b^-1 belong to N so that N is a group. Furthermore, for an arbitrary element g of G we have

( g^-1ag)' = g'^-1a'g' = g'^-1e'g' = g'^-1g' = e' ;

i.e. g'^-1ag lies in N for every g of G and every a of N, and from this it follows obviously that N is a normal subgroup. This proves the first statement of the theorem.

To prove the second statement we choose in G an arbitrary element g and consider the set U of all those elements u of G whose image u' coincides with the image g' of g. Suppose that u is in gN, i.e., u = gn where n ∈ N, so that u' = g'n' = g'e' = g'. Therefore gN ⊂ U. Conversely, if u' = g', then (g^-1u)' = g'^-1u' = g'^-1g' = e', i.e., g^-1u = n, where n is an element of N. Hence u = gn and so U ⊂ gN. From gN ⊂U and U ⊂ gN it follows that U = gN.

Finally, the third statement of the theorem is obvious: To arbitrary cosets gN, hN of the factor group G/N there correspond in H the elements g',h', and to the product of the cosets, by the formula

gN ∙ hN = ghN,

there corresponds (gh)' = g'h', as required.

The theorem on homomorphisms shows that every homomorphic image H of a group G is isomorphic to the corresponding factor group G/H. Thus, to within an isomorphism all homomorphic images of a given group G are exhausted by its distinct factor groups.

Mathematics, Its Content, Methods and Meaning, III, p. 304

References

James and James. Mathematics Dictionary.

Ayres. Modern Algebra. Chap. 9

Birkhoff, MacLane, A Survey of Modern Algebra. Chap. vi

Beaumont, Ball. Intro. to Modern Algebra and Matrix Theory. Chap. IV

Van der Waerden. Modern Algebra. Chap. 2

Mathematics, Its Content, Methods and Meaning. Chap. XX

Fang. Abstract Algebra.