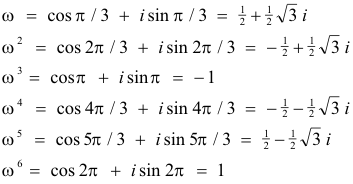
Website owner: James Miller
GROUPS, SUBGROUPS, COMPLEXES, COSETS, TRANSFORMS, NORMAL SUBGROUPS, QUOTIENT GROUPS, COMMUTATORS, COMPOSITION SERIES, ISOMORPHISMS, HOMOMORPHISMS, AUTOMORPHISMS
Groups. The concept of a group arose out of the study of the abstract properties of mathematical systems. This study was closely associated with the theory of permutations and investigations into the solvability of polynomial equations of degree five and higher by radicals as conducted by Galois and others. The question of the solvability of polynomial equations of degree five and higher is closely connected to the concept of a permutation group.
A group is a mathematical system possessing certain abstract mathematical properties. These properties are defined in terms of axioms. Any mathematical system which possesses the required properties qualifies as a group. The formal definition of a group is as follows:
Def. Group. A set G of elements on which a binary operation (usually called multiplication) is defined which satisfies the following conditions:
G1 Closure.
ab is in G for every a,b in G
G2 Associative law holds.
a(bc) = (ab)c for all a,b,c in G
G3 Existence of an identity element.
G contains an element e such that ea = ae = a for every a in G.
G4 Existence of inverse elements.
For every element a in G there exists an inverse element a-1 in G such that a a-1 = a-1a = e
Theorem. In a group a left inverse is also a right inverse and a left identity is also a right identity. Proof
Definitions of an, a0, and a-n. Given a group G
an = aaa ... a to n factors; where n is a positive integer
a0 = e (e is the identity element)
a-n = (a-1)n = a-1 a-1 a-1 ... a-1
for any element a in G.
Examples of groups.
1. The set I of all integers ( ... -3, -2, -1, 0, 1, 2, 3, ... ) where the group operation is ordinary addition. This system meets all the four axiomatic requirements of a group. It is closed and it is associative. An identity element exists, namely the number 0, such that for each a in I, 0 + a = a + 0 = a. And for every element a in I there is an inverse element -a such that a + (-a) = 0.
2. The set R of all rational numbers under the operation of ordinary multiplication. This mathematical system has all the four properties of a group. It is closed and associative. An identity element exists, namely the number 1, such that for each a in R, 1 · a = a · 1 = a. And for every element a in R there is an inverse element 1/a such that a · (1/a) = 1.
3. The set of all rational numbers under the operation of ordinary addition. It can be seen to have all the four properties of a group.
4. The six sixth roots of unity
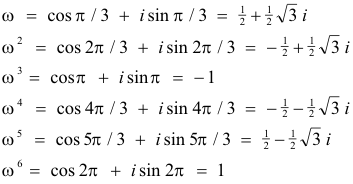
form a group consisting of six members in which the group operation is ordinary multiplication. One can confirm that it has all the four properties of a group.
5. Group of symmetries. The set of all rigid motions that transform a given geometric figure onto itself. For example, the symmetries of a circle consist of all rotations in the plane around the center and of all 180o reflections through space about a diameter. There are eight symmetries of a square: rotations in the plane of the square around its center of 0o, 90o, 180o, and 270o; reflections through space of 180o about the two diagonals; reflections through space of 180o about the two perpendicular bisectors of pairs of opposite sides. The symmetries of a geometric figure form a group if the product of two symmetries S1 and S2 is defined as the symmetry obtained by first applying S1 and then applying S2. The symmetries of a polygon or a polyhedron can be described as permutations of the vertices, so that such groups of symmetries are subgroups of permutation groups. James and James. Mathematics Dictionary
An example of a mathematical system that is not a group is the set I of all integers under the operation of ordinary multiplication. It does not meet the requirement of axiom 4) for the existence of inverse elements.
Theorems. Given any group G and elements a, b, c, ...
1] Cancellation law. If ac = ad or ca = da then c = d.
2] Both of the equations ax = b and xa = b have a unique solution for all a,b in G.
3] For every a in G, the inverse of the inverse of a is a i.e. (a-1)-1 = a
4] (ab)-1 = b-1a-1 for every a,b in G
5] (abc...pq)–1 = q-1p-1....c-1b-1a-1 for every a,b,c, ... ,p,q in G
6] aman = am+n
(am)n = amn
where m and n are integers
Some definitions:
Abelian (or Commutative) Group. A group in which the commutative law holds i.e. ab = ba for all members a,b of the group.
Cyclic group. A group for which all members are powers of one member. A cyclic group may have a finite number of members or an infinite number.
In a cyclic group there exists some member “a” such that all other members of the group are
some power am of a where m
![]() I (I is the set of all integers). The element a is called a generator
of the group.
I (I is the set of all integers). The element a is called a generator
of the group.
A cyclic group is necessarily Abelian.
Examples of cyclic groups:
1) The six sixth roots of unity with ordinary multiplication as the group operation.
2) The set
{ .... -12, -9, -6, -3, 0, 3, 6, 9, 12, ....}
with addition as the group operation. It is generated by the element 3. It is a cyclic group with an infinite number of members. See the following:
Subgroups of the additive group of integers
Finite group. A group having only a finite number of members.
Examples: finite cyclic groups, dihedral groups, permutation groups.
Infinite group. A group having an infinite number of members.
Examples: 1) the set of all integers with addition as the group operation; 2) the set of all mxn matrices over some field F with respect to the operation of matrix addition. 3) the set of all nonsingular nxn matrices over some field F with respect to the operation of matrix multiplication.
Order of a group. The number of members in a group. If it is a finite group the order is some positive integer. Otherwise the order is infinite.
Example: The five fifth roots of unity form a cyclic group of order 5.
Order (or period) of a member of a group. The order of a member “a” of a group is the least positive integer n, if one exists, for which an = e (where e is the identity element). Also called the period.
Example. In the group consisting of the six sixth roots of unity with multiplication as the group
operation, the member
![]() is of order (or period) 3, since
is of order (or period) 3, since
![]()
and
![]()
Complex Any non-empty subset of a group G.
Equality of complexes. The equality of complexes is the equality of sets; that is, two complexes are equal if and only if they contain the same elements.
Product of two complexes. The product HK of two complexes H and K of a group G is the set of all elements hk ∈ G where h ∈ H and k ∈ K.
Example. Let H = {h1,h2}, K = {k1,k2,k3}. Then HK = {h1k1, h1k2, h1k3, h2k1, h2k2, h2k3}
The “multiplication” operation for the product hk is whatever the binary operation is in group G.
Subgroup. A nonempty subset of a group G is a subgroup of G if it is itself a group with respect to the binary operation defined on G.
Example of subgroups. In the group G
G = {ω, ω2, ω3, ω4, ω5, ω6 = 1}
consisting of the six sixth roots of unity with ordinary multiplication as the group operation
the groups G' = {ω3, ω6} and G'' = { ω2, ω4, ω6} are subgroups. Here ω3 = -1 and ω6 = 1 are square roots of 1 and ω2, ω4, ω6 are cube roots of 1.
Proper and improper subgroups. Every group G has at least two subgroups: 1) The whole group G (since a group G is regarded as a subgroup of itself), and 2) The group consisting of the identity element alone (the identity element meets the axiomatic requirements for being a one-element group). These two subgroups are called improper subgroups. All other subgroups are called proper subgroups.
Subgroup generated by a set of elements. Let S = { a, b, c, ... ,g } be an arbitrarily chosen set of elements a,b,c, ... ,g of a group G. Let S* consist of all finite products of the elements of S, their inverses and powers i.e. S* = {abc ...ga-1b-1c-1 ... am bncp .... gq} where m,n,p, ... q are any integers. Then S* represents the smallest subgroup of G which contains the elements of S. Subgroup S* is said to be generated by the elements a,b,c, ... ,g of G.
Def. Free group. A group is free if the group has a set of generators such that no product of generators and inverses of generators is equal to the identity unless it can be written as a product of expressions of type a⋅a-1. E.g., if a free group has generators a and b, then expressions of type ab, aba, a-1babbab-1, etc. are all distinct members of the group. An Abelian group is free if no product of generators and inverses of generators is equal to the identity unless it can be reduced to a product of expressions of type a⋅a-1 by use of the commutative law. James and James. Mathematics Dictionary
Def. Transformation group. A set of transformations which form a group.
Coset. coset of a subgroup H of a group G. Let H = {h1, h2, ... ,hm} be a subgroup of a group G. Then for any a in G the complex product aH = {ah1,ah2, ... ,ahm} is called a left coset of H in G and the complex product Ha = {h1a, h2a, ... ,hma} is called a right coset of H in G. In other words, a left coset of H in G consists of the set of all products ah for all h in H and any fixed element a in G. A right coset of H in G consists of the set of all products ha for all h in H and any fixed element a in G.
Theorem. Any two left (or right) cosets of a subgroup H of a group G are either identical or have no elements in common. The j distinct left (or right) cosets of H partition G into j mutually disjoint sets.
Def. Transform. transform of an element of a group. Given group G. The transform
Tx(a) of an element a
![]() G by an element x
G by an element x
![]() G is the element a' = x -1ax. The transform is a
function or mapping that maps an element a
G is the element a' = x -1ax. The transform is a
function or mapping that maps an element a
![]() G into an element a' = x -1ax
G into an element a' = x -1ax
![]() G.
G.
Normal (or invariant) subgroup. A subgroup H of a group G for which the transform of any element of H by any element of G is in H. A subgroup is normal if and only if all its right cosets are also left cosets.
Syn. invariant subgroup, normal divisor.
The cosets of normal subgroups form groups called quotient groups under the operation of complex multiplication.
Quotient group G/H. The quotient group of a group G by an invariant subgroup H is the group (denoted by G/H) whose elements are the cosets of H (these cosets are also equivalence classes if one defines x and y to be equivalent if xy -1 belongs to H). Multiplication on the group is complex multiplication (i.e. multiplication as defined for complexes). The unit element of G/H is H and the inverse of a coset aH is the coset a -1H.
Syn. factor group
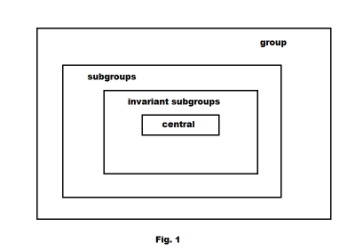
Central of a group. The set of all elements of the group which commute with every element of the group. Stated differently, the central of a group G is the set of all x in G such that xg = gx for every element g of G. The central is an invariant subgroup, but may be contained properly in an invariant subgroup. See Fig. 1. James and James. Mathematics Dictionary
Syn. Center of a group
Simple group. A group that has no invariant subgroups other than the identity alone and the whole group. A group which is not simple is called composite.
Commutator. commutator of elements of a group. The commutator of two elements a and b of a group is the element a-1b-1ab, or the element c such that bac = ab. The group of all elements of the form c1c2, ... cn, where each ci is the commutator of some pair of elements, is called the commutator subgroup. The commutator subgroup of an Abelian group contains only the identity element. A group is said to be perfect if it is identical with its commutator subgroup. A commutator subgroup is an invariant subgroup and the factor group formed with it is Abelian. James and James. Mathematics Dictionary
Def. Maximal invariant subgroup. An invariant subgroup H of a group G is called maximal provided there exists no proper invariant subgroup K of G having H as a proper subgroup.
Def. Composition series. For any group G a sequence of its subgroups
G, H, J, K, ... ,U = {e}
is called a composition series for G if each element except the first is a maximal invariant subgroup of its predecessor. The groups G/H, H/J, J/K, ... are called the quotient groups of the composition series.
Every finite group has at least one composition series.
Groupoid. A set S of elements on which a binary operation is defined which is closed under the operation.
Semigroup. A groupoid on which the associative law holds.
Monoid. A semigroup with an identity element.
Examples of various algebraic systems
Def. Isomorphism. Let M be a set of elements closed with respect to the binary operation ∙ and let N be a set of elements closed with respect to the binary operation ∘. An isomorphism between M and N is a one-to-one correspondence between M and N whereby if elements x and y of M correspond to x* and y* of N then x∙y of M corresponds to x*∘y* of N.
Alternate equivalent definition: An isomorphism between two sets M and N with binary operations ∙ and ∘ respectively is a one-to-one onto mapping f :M→ N whereby f(x∙y) = f(x)∘f(y) for all x,y in M.
The significance of the two sets M and N being isomorphic is that if they are isomorphic they have exactly the same algebraic properties, they are equivalent algebraically.
Theorem. Let sets M and N with binary operations ∙ and ∘ respectively be isomorphic. Then
1. ∙ is associative if and only if ∘ is associative
2. ∙ is commutative if and only ∘ is commutative
3. M contains an identity for ∙ if and only if N contains an identity for ∘. In addition the identities coincide.
Def. Automorphism. Let set M be closed with respect to the binary operation ∙. An automorphism of M is a one-to-one mapping of M onto itself (f :M→M,) such that f(x∙y) = f(x)∙f(y) for all x,y in M.
Isomorphisms. Two axiomatically-defined abstract mathematical systems as, for example, two groups, rings, linear spaces , etc. are said to be isomorphic to each other if they are equivalent structurally, algebraically, in their internal workings; with like elements corresponding in a one-to-one fashion, the differences between them being only superficial ones as in the names we give the elements and the way we denote the law of combination. The mathematical condition that must be met for two groups to be isomorphic to each other is given in the following definition:
Def. Isomorphic groups. An isomorphism between two groups G and G* is a one-to-one correspondence between their elements that preserves group multiplication. Specifically it is a correspondence where if elements x and y of G correspond to x* and y* of G* then xy corresponds to x*y*.
Note. An alternative, but equivalent definition is: An isomorphism between two groups G and G* is a one-to-one mapping f :G→G* where f(xy) = f(x)f(y) for all x,y in G.
If the condition given by the definition is met we then say that the operation of multiplication is preserved between the two groups. Identity elements will correspond and inverse elements will correspond. The condition insures that the two groups are equivalent structurally and algebraically.
Homomorphism. As with an isomorphism, a homomorphism is also a correspondence between two mathematical structures that are structurally, algebraically identical. However, there is an important difference between a homomorphism and an isomorphism. An isomorphism is a one-to-one mapping of one mathematical structure onto another. A homomorphism, in its full generality, is a many-to-one mapping of one structure onto another. Where an isomorphism maps one element into another element, a homomorphism maps a set of elements into a single element. Its definition sounds much the same as that for an isomorphism but allows for the possibility of a many-to-one mapping. An isomorphism is actually a special case of a homomorphism.
For the case of homomorphisms between groups the definition is as follows:
Def. Homomorphic groups. A homomorphism from a group G to a group G* is a mapping from G onto G* where if elements x and y of G correspond to x* and y* of G*, then xy must correspond to x*y*.
Note. An alternative, but equivalent definition is: An homomorphism between two groups G and G* is a mapping f :G→G* where f(xy) = f(x)f(y) for all x,y in G .
The idea of a homomorphism is closely connected with the idea of quotient groups and is best illustrated by them. Quotient groups are groups whose elements are sets -- namely cosets of the normal group of some group. The cosets of any normal subgroup H of a group G form a group under complex multiplication and this group is called the quotient group (or factor group) of G by H and is denoted by G/H. The normal subgroup H plays the role of the identity in the quotient group. The following theorem is fundamental in the theory of homomorphic mappings:
Theorem. Under homomorphic mapping of an arbitrary group G onto a group G', the set N of elements of G that are mapped into the identity element e' of G' is a normal subgroup of G; the set of elements of G that are mapped into an arbitrary fixed element of G' is a coset of G with respect to N, and the one-to-one correspondence thus established between the cosets of G with respect to N and the elements of G' is an isomorphism between G' and the quotient group G/N.
Mathematics, Its Content, Method and Meaning, III. p. 304
From this theorem we see that under this homomorphism all the elements in a particular coset are imaged into a single element in G'. Elements from separate cosets are imaged into separate elements in G'. Thus we see that under a homomorphic mapping, on transition from G to G', distinct elements of G coalese into a single element of G'. Classes or sets of elements map into single elements.
Def. Kernel of a homomorphism. If a homomorphism maps a group G onto a group G*, then the kernel of the homomorphism is the set N of all elements in G which map onto the identity element of G*. Then N is a normal subgroup of G and G* is isomorphic with the quotient group G/N. If a homomorphism maps a ring R onto a ring R*, then the kernel of the homomorphism is the set I of elements in R which map onto the zero element of R*. The kernel I is an ideal and R* is isomorphic with the quotient ring R/I. James and James. Mathematics Dictionary
Automorphism. An automorphism is an isomorphism of a set with itself. In the case
of groups it is an isomorphism between subgroups of a group
Def. Automorphism of a group. An automorphism of a group G is a one-to-one mapping f :G→G (i.e. a one-to-one correspondence between elements of G) where f(xy) = f(x)f(y) for all x,y in G.
.
***************************************************
Theorems.
1] If H is a subgroup of G, then the identity in H is the identity e in G, and the inverse of an element a in H is its inverse a-1 in G.
2] A nonempty subset H of a group G is a subgroup of G if and only if : 1) it is closed with respect to the group operation, and 2) it contains the inverse of each of its elements.
3] A nonempty subset H of a group G is a subgroup of G if and only if a-1b is in H for all a,b in H. Proof
4] Let a be an element of a group G. The set H = {an: n is an integer} of all integral powers of a is a subgroup of G
5] If S is any set of subgroups of a group G, the intersection of these subgroups is also a subgroup of G.
6] Every subgroup of a cyclic group is itself a cyclic group.
7] An element at of a finite cyclic group G of order n is a generator of G if and only if the greatest common denominator of n and t is 1.
8] Lagrange’s theorem If G is a subgroup of a group H of finite order, then the order of G divides the order of H.
9] Jordan-Holder Theorem. For any finite group with distinct composition series, all series are of the same length, i.e. have the same number of elements. Moreover, the quotient groups for any pair of composition series may be put into one-to-one correspondence so that corresponding quotient groups are isomorphic.
10] Under an isomorphism between two groups, the identity elements correspond and the inverses of corresponding elements correspond.
11] The relation “G is isomorphic to Gʹ” is a reflexive, symmetric, and transitive relation between groups.
12] Every finite group of order n is isomorphic with a permutation group on n letters.
13] Every cyclic group of infinite order is isomorphic to the additive group I of integers.
14] Every cyclic group of finite order is isomorphic to the additive group I/(n) of integers modulo n.
References.
James and James. Mathematics Dictionary.
Ayres. Modern Algebra. Chap. 9
Birkhoff, MacLane, A Survey of Modern Algebra. Chap. VI
Beaumont, Ball. Intro. to Modern Algebra and Matrix Theory., Chap. IV
Van der Waerden. Modern Algebra. Chap. 2
Mathematics, Its Content, Methods and Meaning. Chap. XX
Fang. Abstract Algebra.
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life