Simply connected regions, work, conservative force fields, scalar potential, irrotational vector

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

SIMPLY CONNECTED REGIONS, WORK, CONSERVATIVE FORCE FIELDS, SCALAR POTENTIAL, IRROTATIONAL VECTOR

Def. Connected region. A region R is said to be connected if any two points of R can be joined by an arc where every point on the arc belongs to R.

Def. Simply connected region. A region R is said to be simply connected if every closed curve in R can be continuously shrunk to a point in R without leaving R. If a region is not simply connected it is said to be multiply connected.

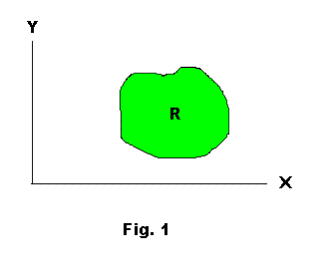
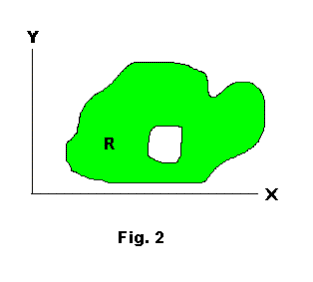
The above definition applies to regions in a plane. It also applies to regions in space. The region shown in Fig.1 is simply connected. The region shown in Fig.2 is multiply connected since closed curves can be drawn in it that cannot be shrunk to a point without leaving the region. As for examples of regions in space that are simply connected we name the following:

Examples of regions in space that are simply connected: the interior of a sphere, the region exterior to a sphere, and the space between two concentric spheres.

Examples of regions in space that are not simply connected: the interior of a torus, the region exterior to a torus, and the space between two infinitely long coaxial cylinders.

Theorem 1. Let C be a space curve running from some point A to another point B in some region Q of space. Let curve C be defined by the radius vector R(s) = x(s) i + y(s) j + z(s) k where s is the distance along the curve measured from point A. Let F(x, y, z) = f₁(x, y, z) i + f₂(x, y, z) j + f₃(x, y, z) k represent a force field defined over the region. Let T denote the unit tangent to the curve at point (x, y, z). Then

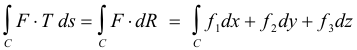
where

represents the work done in moving an object along the curve from point A to point B.

Def. Total differential. The total differential of a function of several variables, f(x₁, x₂, ... x_n), is the function

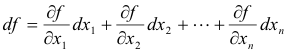
which is a function of the independent variables x₁, x₂, ... , x_n, d x₁, dx₂, ... , dx_n. Each of the terms

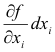
is a partial differential.

Syn. Exact differential

Conditions for a line integral to be independent of path. Let Q be a simply connected region of space. The value of the line integral

taken along some path (i.e. space curve) from point P₁:(x, y, z) to point P₂:(x, y, z) within Q will be independent of the particular path chosen if the integrand

P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz

is a total (or exact) differential of some function Φ. If the integrand is an exact differential then there will exist some function Φ(x, y, z) such that

dΦ = P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz

In this case

where the function Φ(x, y, z) is a scalar point function called the potential function.

The integrand of the line integral will be an exact differential if and only if

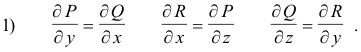
This condition is equivalent to curl F = 0.

If F represents a force field and the line integral is independent of path we say that the force field is a conservative field.

Theorem 2. Let Q be a simply connected region of space. A necessary and sufficient condition that

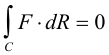
for every closed curve C in Q is that ∇×F = 0 identically over Q.

This theorem follows from Stokes’ Theorem

for if ∇×A = 0 in Stokes’ Theorem then

Theorem 3. A necessary and sufficient condition that the value of the integral

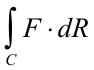
be independent of path in a simply connected region Q is that ∇×F = 0 identically over Q.

This follows from Theorem 2 because if we go from point A to point B by one path and then go from point B back to point A by another path we have made a closed circuit.

Theorem 4. Let Φ(x, y, z) be a scalar point function over a simply connected region Q of space. Let F be the gradient of Φ i.e. F = ∇Φ. Then curl F = 0 over Q. In other words, curl grad Φ = ∇×(∇Φ) = 0 at each point of Q.

Proof

Necessary and sufficient condition that the curl of a vector function vanish within a region. Let vector point function F have continuous first derivatives within a simply connected region Q. Then a necessary and sufficient condition that curl F = 0 everywhere within Q is that F be the gradient of some scalar point function Φ (i.e. that there exists some scalar point function Φ such that F = grad Φ). Such a function Φ is called a scalar potential.

Irrotational field. A vector point function F is said to be irrotational in a region R if curl F = 0 everywhere in R.

Theorem 5. Let F(x, y, z) be the gradient of the scalar point function Φ(x, y, z) defined over a simply connected region Q of space i.e. F = ∇Φ over region Q. Let F possess continuous first partial derivatives at all points of Q. Then

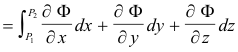
Thus if F = ∇Φ, the integral

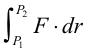
depends only on the end points P₁ and P₂ and is independent of the path joining them.

Theorem 6. Let Q be a simply connected region of space and let F₁(x, y, z), F₂(x, y, z), F₃(x, y, z) be scalar functions of position defined over Q. A necessary and sufficient condition that F₁dx + F₂dy + F₃dx be an exact differential within Q is that ∇×F = 0 at all points within Q where F = F₁i + F₂ j + F₃ k.

Theorem 7. Let F = u(x, y, z) i + v(x, y, z) j + w(x, y, z) k be a vector point function possessing continuous first partial derivatives at all points of a simply connected region Q of space. Then the following statements are all equivalent; each one of them implies each of the others.

3. F∙dr = u dx + v dy + w dz is an exact differential within Q

4. F is the gradient of the scalar point function

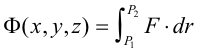
within Q i.e. F = ∇Φ over region Q.

5. The curl of F vanishes identically at all points within Q

Def. Conservative force field. A force field such that the work done in moving a particle from one position to another is independent of the path along which the particle is moved. In a conservative field the work done in moving a particle around any closed path is zero. If the work done on the particle is represented by a line integral

where F_x, F_y, and F_z are the Cartesian components of force in a conservative field, then the integrand in an exact differential. The gravitational and electrostatic fields of force are examples of conservative fields, whereas the magnetic field due to current flowing in a wire and fields involving frictional effects are non-conservative.

James & James, Mathematics Dictionary.

If F is a conservative field over a region Q of space then curl F = 0 within Q (i.e. F is irrotational within Q). Conversely, if curl F = 0 within Q, then F is conservative within Q.

Def. Irrotational vector in a region A vector point function whose integral around every reducible closed curve in the region is zero. The curl of a vector is zero at each point of a region if, and only if, it is the gradient of a scalar function (called a scalar potential); i.e. ∇×F ≡ 0 if and only if F = -∇Φ for some scalar potential Φ.

James & James, Mathematics Dictionary.

Scalar potential. A vector field V which can be derived from a scalar field Φ so that V = ∇Φ is called a conservative vector field and Φ is called the scalar potential.

References.

Spiegel. Vector Analysis.

Spiegel. Adv. Calculus.

Wylie. Advanced Engineering Mathematics.

James & James, Mathematics Dictionary.