Proof of Green's Theorem in the Plane

SolitaryRoad.com

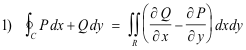
Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

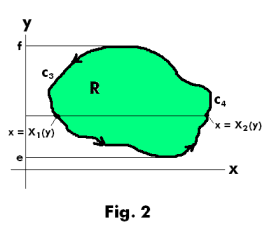
Prove. Let P(x, y) and Q(x, y) be continuous and have continuous partial derivatives in a region R and on its boundary C. Then

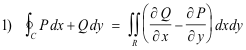
Proof. There are some difficulties in proving Green’s theorem in the full generality of its statement. However, for regions of sufficiently simple shape the proof is quite simple. We will prove it for a simple shape and then indicate the method used for more complicated regions. We will require such a shape that lines parallel to either x or y axis cut the boundary C of the region at no more than two points.

We shall prove the following two statements:

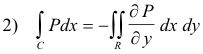
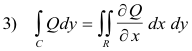
This will conclude the proof since the sum of 2) and 3) gives 1).

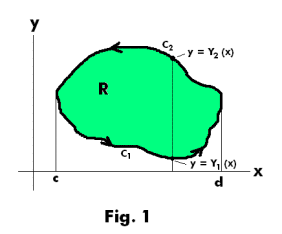
We shall now proceed to prove 2) and shall utilize Fig. 1. Let the boundary of region R consist of a lower curve y = Y₁(x) and an upper curve y = Y₂(x) as shown. Let c₁ and c₂ denote the lower and upper curves. Then

Computing the line integral for C₁

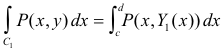
where c and d are the limits shown in the figure.

Similarly, for C₂ we have

Thus

Now let us consider the double integral in the right member of 2). It can be written as

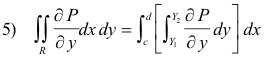
By the Fundamental Theorem of Integral Calculus the integral within the brackets can be written as

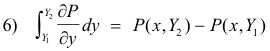
and 5) becomes

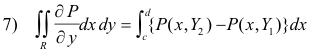
From 4) and 7) we get

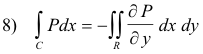
which is 2) above.

In a completely similar way we can obtain 3) above using Fig. 2. Then adding 2) and 3) we get 1).

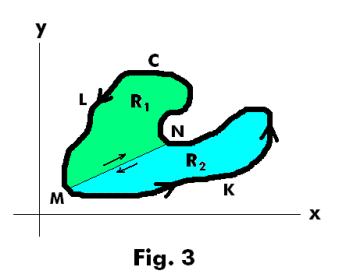
How do we extend the proof of the theorem to more complicated shapes? We divide the more complicated shapes up into simpler regions of the type we have just considered using cuts such as the cut MN shown in Fig. 3. These cuts add to the boundary traversed by the amount of the cuts, traversed twice in opposite directions. Because they are traversed in opposite directions, the line integrals along the cuts cancel each other out, the net boundary traversed remains the same, and the theorem remains unchanged. More explicitly, referring to Fig. 3 we have

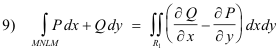
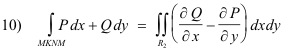
Adding the left sides of 9) and 10), omitting the integrands P dx + Q dy, we get

using the fact that

Adding the right sides of 9) and 10), omitting the integrands, we get

Consequently, from 11) and 12),

For more complicated regions we may need to construct more cuts dividing the region into more subregions.

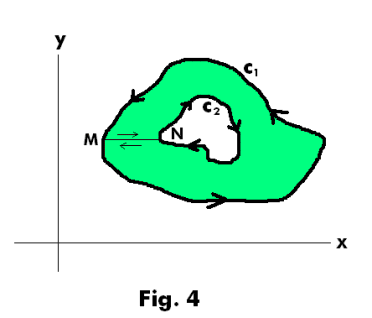
Suppose the region is multiply-connected as shown in Fig. 4. How do we extend the proof to multiply-connected regions? For this we create a cross-cut MN, connecting the exterior and interior boundaries as shown in the figure, thus converting the region into a simply-connected region. The amount of boundary traversed is increased by the cross-cut MN, traversed in opposite directions. Because it is traversed in opposite directions the line integrals on the cross-cut cancel each other out and the net boundary traversed remains the same, namely c₁ plus c₂, and the theorem remains the same.

References

Spiegel. Complex Variables. (Schaum)

Taylor. Advanced Calculus.