Space curves, tangent vector, principal normal, binormal, curvature, torsion, Frenet-Serret formulas, spherical indicatrices

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

SPACE CURVES, TANGENT VECTOR, PRINCIPAL NORMAL, BINORMAL, CURVATURE, TORSION, FRENET-SERRET FORMULAS, SPHERICAL INDICATRICES

Def. Space curve. We can think of a space curve as a path of a moving point. The definition of a space curve is essentially an analytical implementation of this view. A space curve is defined parametrically as the graph of parametric equations

x = f(t)

1) y = g(t)

z = h(t)

where the functions f, g and h are continuous and the range of the parameter t is some interval (finite or infinite) of the real axis. In vector language a space curve is defined as the graph of points traced out by a position vector

2) R(t) = f(t) i + g(t) j + h(t) k

where the functions f, g and h are continuous and the range of the parameter t is some interval (finite or infinite) of the real axis. The positive direction of a space curve is the direction of increasing t. i.e Δs/Δt > 0.

If we interpret t as time, 1) can be regarded as defining the path of a moving point. The point may pass through the same point in space several times which means that the curve may intersect itself. This definition that we have given gives a curve that is very general and one that may not be very smooth. For example, it could include things like the track of a tiny particle in Brownian movement over a long period of time (a very random path going first in one direction and then abruptly changing to another direction — randomly and suddenly changing from one direction to another).

Def. Arc of a curve. A curve that does not intersect itself, which has two distinct ends, and which can be represented in the form 1) with a finite range of the parameter t, say a t b, where a < b. A semicircle is an arc but an entire circle is not.

Def. Closed curve. A curve that is defined by 1) with a finite range of the parameter t, say a t b, in which the points corresponding to t = a and t = b are coincident.

Def. Simple closed curve (or Jordan curve). A closed curve without self-intersections.

The prototype of an arc is the unit interval 0 x 1, while the prototype of a simple closed curve is the unit circle x² + y² = 1. Continuous deformation (bending, twisting, stretching, shrinking) of an arc leaves it still an arc and the same can be said about simple closed curves.

Def. Smooth curve. A curve is said to be smooth if two conditions are met;

a) the curve does not intersect itself

b) the curve has a tangent at each point whose direction varies continuously as the point moves along the curve.

The second condition is satisfied if the functions f, g, and h of 1) above have continuous derivatives which do not vanish together for any value of t.

Important fundamental relationships. The differential of arc length ds is related to dx, dy, and dz by

ds² = dx² + dy² + dz² .

Let C be a smooth arc represented by a vector function f(t) = x(t) i + y(t) j + z(t) k, a t b. Let s be the arc length measured along C from point t = a to a variable point t. Then the following holds:

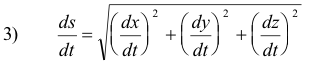
(which is obtained directly from the formula ds² = dx² + dy² + dz² by dividing by dt²).

Length of a smooth arc. Let C be a smooth arc represented by a vector function f(t) = x(t) i + y(t) j + z(t) k, a t b . Then its length, from point t = a to t = b, is given by

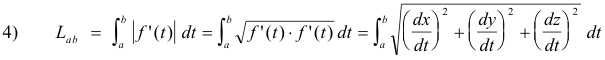
The distance along the curve, measured from point t = a to some variable point t, is given by

(which is obtained by replacing the fixed upper limit b in 4) with t)

Unit tangent vector. Let a space curve C be given by

5) R(s) = x(s) i + y(s) j + z(s) k

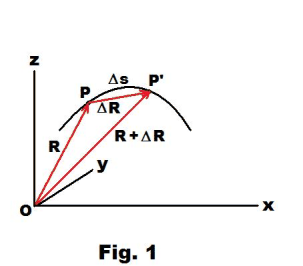
where the parameter s represents the arc length measured from some fixed point on the curve. Then the unit tangent vector to the curve at a particular point P is given by

6) T = dR/ds

That this is so can be seen from Fig. 1 which shows R and R + ΔR at points P and P'. The quotient ΔR/Δs is a vector along the line of the chord PP'. Since the length of ΔR is the length of the chord PP', we see that when P' approaches P the limit of the length of ΔR/Δs is unity. Furthermore, the limiting direction of PP' is that of the tangent at P. Therefore

From 5) we obtain

Direction cosines of the unit tangent vector. The direction cosines of the unit tangent vector at a point P are given by the x, y and z components of the vector.

Principal normal. The principal normal, denoted by N , at a point P on a curve C, is a unit vector in the direction of dT/ds (providing dT/ds is not zero, in which case the principal normal is not defined). The principal normal is necessarily perpendicular to the unit tangent vector T. From 7) above we obtain

Curvature of a curve at point P. The curvature κ of a curve at a point P is given by the magnitude of dT/ds:

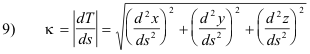
Thus

10) dT/ds = κN

Radius of curvature. The radius of curvature ρ is the reciprocal of the curvature:

11) ρ = 1/κ

Center of curvature. The tip of the vector ρN, drawn from point P as initial point, is called the center of curvature of the curve at point P.

Binormal. The vector B = T N .

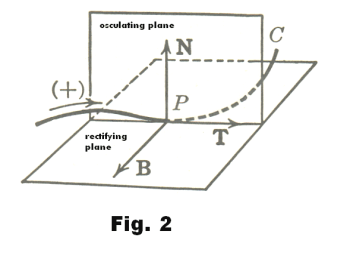
Moving trihedral. The three mutually perpendicular unit vectors T, N and B form a right-handed triad associated with each point P of a space curve. This trihedral represents a localized right-handed coordinate system that moves as one moves along a curve. It is called the moving trihedral. See Fig. 2. In this moving trihedral the plane containing the tangent T and principal normal N is called the osculating plane, the plane perpendicular to the tangent at P, i.e. the plane containing the principal normal N and binormal B, is called the normal plane, and the plane containing the tangent T and binormal B is called the rectifying plane. The osculating plane represents the plane of the curve in the immediate vicinity of the point.

Normal plane. The normal plane is the plane perpendicular to the tangent vector T at point P. The lines in the normal plane that go through P are known as the normals to the curve at P. Thus the name normal plane. The normal plane contains two important normals, the principal normal and the binormal.

Osculating plane. The osculating plane of a curve C at a point P is the plane that contains the unit tangent vector T at P and the principal normal vector dT/ds where s is the distance along the curve (the osculating plane does not exist if if dT/ds = 0 e.g., if the curve is a straight line). The osculating plane is the plane in the limiting position, if it exists, of the plane through the tangent to C at the point P, and through a variable point P' on C, as P' P along C.

James / James. Mathematics Dictionary.

Def. Twisted curve. A curve that does not lie in a single plane.

Torsion. The torsion τ at a point P on a curve is given, to within sign, by the magnitude of the vector dB/ds. The vector dB/ds is perpendicular to vectors T and B and thus is some multiple of vector N. The sign of τ is chosen so that dB/ds = -τN. The torsion measures, to some extent, the amount by which the curve is twisted.

Note. Some authors define torsion by the formula dB/ds = τN instead of dB/ds = -τN and some use 1/τ rather than τ to denote torsion.

If P is a fixed point, and P' a variable point, on a directed space curve C, Δs the length of arc C from P to P', and Δψ the angle between the positive directions of the binormals of C at P and P', then the torsion τ of C at P is defined, to within sign, by

James / James. Mathematics Dictionary.

Proof.: The vector dB/ds is perpendicular to vectors T and B and thus is some multiple of vector N.

Radius of torsion. The radius of torsion is defined as the quantity σ = 1/τ.

Intrinsic equations of a space curve. For a particular curve C, the curvature κ and torsion τ are functions κ(s) and τ(s) of arc length s as measured from some fixed point on C. As we move along curve C the tangent is turning in the direction of the normal at a rate determined by the curvature κ(s) while the osculating plane rotates around the tangent with a speed determined by the torsion τ(s). It can be shown that two curves with the same curvature and torsion as functions of arc length are identical except for position and orientation in space (i.e. one of them can be rigidly moved so as to coincide with the other). Thus the curvature κ(s) and torsion τ(s) describe all the essential, invariant properties of the curve. The equations

κ = κ(s)

τ = τ(s)

are called the intrinsic or natural equations of the curve.

Frenet-Serret formulas. The Frenet-Serret formulas are

1] dT/ds = κN

2} dN/ds = τB - κT

3] dB/ds = -τN

where T, N and B are the three unit vectors of the moving trihedral, the unit tangent, principal normal and the binormal vectors.

Formulas. Let R(t) be a vector function of t and let primes denote differentiation with respect to t.

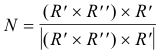
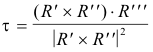
Plane curves. If the curve r = r(t) is a plane curve (not a straight line), the plane of the curve is the osculating plane at every point.

Theorem 1. A necessary and sufficient condition that a curve (not a straight line), be a plane curve is that its torsion be identically zero.

Theorem 2. A necessary and sufficient condition that a curve r = r(t) (not a straight line) be a plane curve is that r' r''∙ r''' = 0.

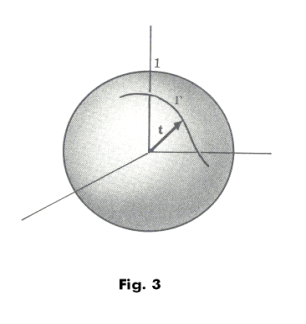
Spherical indicatrices of a space curve.

Spherical indicatrix (or tangent indicatrix) of a space curve. As a point moves along a space curve C envision a unit vector t located at the origin of the coordinate system moving in conjunction with the unit tangent T, always parallel to it. As one moves along C the unit vector t will trace out a curve Γ on a unit sphere centered at the origin. This curve Γ is called the spherical indicatrix (or tangent indicatrix) of curve C. See Fig. 3. If curve C is a plane curve, its spherical indicatrix lies on a great circle of the sphere. Hence, for a space curve, the amount of deviation of the spherical indicatrix from a great circle gives some idea of the amount of deviation of the curve from being a plane curve i.e. of the amount of torsion of the curve.

James / James. Mathematics Dictionary.

Let a curve C be given by

where s represents arc length measured from some point on the curve. Then the spherical indicatrix Γ of curve C is given by

Principal normal indicatrix on a space curve. The curve Γ traced out on a unit sphere located at the origin by a unit vector t moving in conjunction with (parallel to) the principal normal as a point moves along some curve C i.e. it is the same as the tangent indicatrix except that the unit vector t moves in conjunction with the principal normal instead of the unit tangent.

Binormal indicatrix on a space curve. Same as the tangent indicatrix except that the unit vector t moves in conjunction with (parallel to) the binormal instead of the unit tangent.

References.

1) Spiegel. Vector Analysis.

2) James & James, Mathematics Dictionary.

3) Taylor. Advanced Calculus.

4) Graustein. Differential Geometry.