Website owner: James Miller
BASIC CONCEPTS AND CONVENTIONS, VECTORS, SCALARS, OPERATIONS ON VECTORS, VECTOR ALGEBRA, DOT PRODUCT, CROSS PRODUCT, TRIPLE PRODUCT
Vector analysis is concerned with vectors and operations involving them. Its origin lies in the field of physics. In the field of physics some things such as temperature, mass, length, volume, density, time, distance and speed possess only “magnitude”. Other things such as force, velocity and acceleration possess both magnitude and direction. Those things which possess only magnitude are referred to as scalar quantities; those which have both magnitude and direction are referred to a vector quantities.

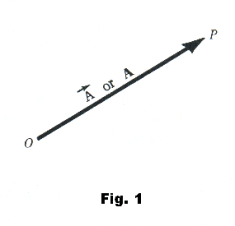
Vectors. A vector is a “directed line segment” (i.e. arrow) representing a quantity such as force, velocity, etc. which possesses both magnitude and direction. The direction of the quantity is given by the direction of the arrow and the magnitude by the length of the arrow. See Fig. 1. The point O of the arrow OP is called the initial point of the vector and the point P the terminal point or tip.
● Two vectors are considered equal if they have the same magnitude and direction regardless of the position of their initial points.
● A vector having direction opposite to that of vector A but having the same magnitude is denoted by -A.
Zero vector. If points O and P of vector OP in Fig.1 are coincident the vector OP is called a zero vector, denoted by 0. It has zero magnitude and no specific direction.
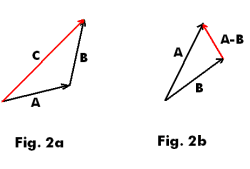
Addition of Vectors. An operation of addition is defined for vectors. The sum of two vectors A and B is the vector C as shown in Fig. 2a. We place the initial point of B at the terminal point of A and C is the vector running from the initial point of A to the terminal point of B. We write C = A + B.
● The difference (A - B) of two vectors A and B is the sum of A and (-B) i.e. A - B = A + (-B). The vector A - B is the vector running from the tip of B to the tip of A. See Fig. 2b. We see from the figure that B + (A - B) = A.
Def. Scalar. A number, as distinguished from a vector. The word “scalar” is used to contrast with the word “vector”. It is customary, in any context where vectors and real numbers are both being discussed, to refer to real numbers as scalars.
Product of a vector A by a scalar m. The product of a vector A by a scalar m is a vector mA with magnitude |m| times the magnitude of A and with direction the same as or opposite to that of A, according as m is positive or negative. If m = 0, mA is the zero vector.
Unit vector. A unit vector is a vector having unit magnitude i.e. a magnitude of 1.
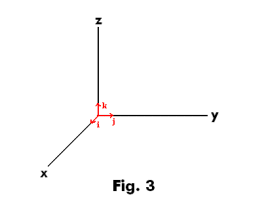
Analytical representation of vectors. Let i, j and k be unit vectors directed along the positive x, y and z axes of a right-handed Cartesian coordinate system as shown in Fig. 3. Let A be a vector whose initial point is located at the origin O and whose terminal point is at coordinates (a1, a2, a3). Then vector A can be represented as
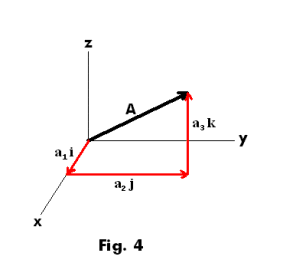
(1) A = a1 i + a2 j + a3 k .
See Fig. 4. The vectors a1 i, a2 j, and a3 k are called the component vectors of A in the x, y and z directions respectively. a1, a2, and a3 are called the x, y and z components of A. The magnitude of A is
![]()
a1, a2, and a3 represent the magnitudes of the projections of vector A on the x, y and z axes respectively.
Any vector may be represented in form (1) above.
A second representation of a vector. A vector is also often denoted simply by an ordered triplet, written either vertically or horizontally, as in
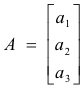
or
A = (a1, a2, a3),
the ordered triplet consisting of the three components.
The sum of two vectors expressed in analytical form is obtained by adding corresponding components i.e. if A = a1 i + a2 j + a3 k and B = b1 i + b2 j + b3 k then
A + B = (a1 + b1) i + (a2 + b2) j + (a3 + b3) k
Def. Absolute value of a vector. The numerical length of the vector; the magnitude of the vector. The absolute value is the square root of the sum of the squares of the components along the axes. The absolute value of a i + b j + c k is
![]()
Syn. Numerical value
Laws of Vector Algebra. If A, B and C are vectors and m and n are scalars, then
1. A + B = B + A Commutative law for addition
2. A + (B + C) = (A + B) + C Associative law for addition
3. mA = Am
4. n(nA) = (mn)A
5. (m + n)A = mA + nA
6. m(A + B) = mA + mB
7. A + 0 = A Additive identity
8. A + (-A) = 0 Additive inverse
These laws enable us to treat vector equations in the same way as ordinary algebraic equations. For example, if A + B = C then by transposing A = C - B.
A much used vector in vector analysis is the position or radius vector.
Position vector (or radius vector). A position vector is a vector that extends from the origin of the coordinate system to some point (x, y, z) in space i.e. the vector
r = xi + yj + zk
or
r = (x, y, z)
Def. Dot product. The dot product A∙B of two vectors A and B is defined as the product of the magnitudes of A and B and the cosine of the angle θ between them i.e.
A∙B = |A| |B| cos θ
Syn. dot product, scalar product, inner product
Note that A∙B is a scalar and not a vector.
● A∙B = a1b1 + a2b2 + a3b3
where A = a1i + a2j + a3k and B = b1i + b2j + b3k
Length of a vector in terms of the dot product. The length of vector X is given by
![]()
Laws valid for dot products:
1] A∙B = B∙A Commutative law
2] A∙(B + C) = A∙B + A∙C Left distributive law
3] (A + B)∙C = A∙C + B∙C Right distributive law
4] m(A∙B) = (mA)∙B = A∙(mB) = (A∙B)m where m is a scalar
5] i∙i = j∙j =k∙k = 1, i∙j = j∙k = k∙i = 0
6] If A∙B = 0 and A and B are not zero vectors, then A and B are perpendicular.
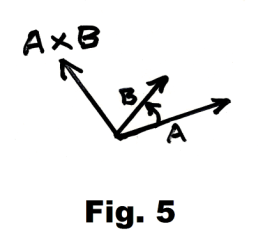
Def. Vector (or Cross) Product. The vector (or cross) product A×B of two vectors A and B is defined as
A×B = |A| |B| sin θ u
where θ is the angle from A to B and u is a unit vector perpendicular to the plane of A and B and so directed that if you curl the fingers of your right hand in the direction that carries A into B, your thumb points in the direction of u (i.e. a right-handed screw driven in the direction of u would carry A into B). See Fig. 5.
If A = a1i + a2j + a3k and B = b1i + b2j + b3k , then
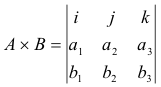
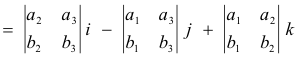
= (a2b3 - b2a3) i + (a3b1 - b3a1) j + (a1b2 - b1a2) k
Laws valid for cross products:
1] A×B = - B×A
2] A×(B + C) = A×B + A×C Left distributive law
3] (A + B)×C = A×C + B×C Right distributive law
4] m(A×B) = (mA)×B = A×(mB) = (A×B)m where m is a scalar
5] i×i = j×j =k×k = 0 i×j = j×k = k×i = 1
6] If A×B = 0 and A and B are not zero vectors, then A and B are parallel..
Triple products. Dot and cross product multiplication of three vectors A, B and C produce meaningful products of the following forms:
1) (A∙B)C
2) A∙(B×C) scalar triple product or box product
3) A×(B×C) vector triple product
Scalar triple product A∙(B×C). Let A = a1i + a2j + a3k , B = b1i + b2j + b3k and C = c1i + c2j + c3k . Then
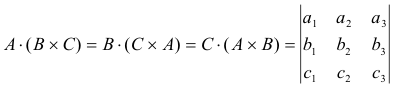
which is equal to the volume of a parallelepiped having A, B and C as edges, or the negative of this volume, according as A, B and C do or do not form a right-handed system.
● A∙(B×C) = (A×B)∙C i.e. the dot and cross can be interchanged without changing the value.
In the scalar triple product A∙(B×C) the parentheses are sometimes omitted and it is written A∙B×C or A×B∙C . It is sometimes denoted simply by [ABC] . It is also called the box product.
Vector triple product. The product A×(B×C) is called the vector triple product.
1] A×(B×C) = B(A∙C) - C(A∙B) = (A∙C)B - (A∙B)C
2] (A×B)×C = (A∙C)B - (B∙C)A
Note that
(A∙B)C
![]() A(B∙C)
A(B∙C)
A×(B×C)
![]() (A×B)×C
(A×B)×C
Generalized identity of Lagrange.
For vectors A, B, C, D the following holds
(A×B)∙(C×D) = (A∙C)(B∙D) - (A∙D)(B∙C)
Identity of Lagrange.
(A×B)∙(A×B) = (A∙A)(B∙B) - (A∙B)2
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life