Rank of a matrix, elementary operations, inverse operations, equivalent matrices, row equivalence, canonical forms, elementary matrices

SolitaryRoad.com

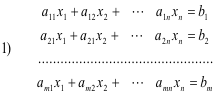
Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Rank of a matrix, elementary operations, equivalent matrices, canonical forms, elementary matrices

Solving systems of simultaneous linear equations. The usual procedure for solving a system of simultaneous linear equations

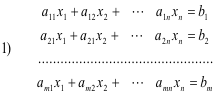
is to go through a succession of steps that reduces the system to a succession of equivalent but simpler systems until we arrive at a system that is easily solved. This succession of steps that transforms it into a succession of simpler equivalent systems is accomplished by applying one or more of the following transformations:

(a) interchanging any two of the equations

(b) multiplying any equation by any non-zero constant

Performing any of these transformations on the system produces an equivalent system that has the same solution as the old. These successive transformations are really transformations on the block of numbers

which defines the system. Thus the problem reduces to one of doing transformations on blocks or arrays of numbers. From this comes the idea of doing various operations on matrices. In particular, from it comes the idea of the elementary row and column operations that one can perform on a matrix that transforms it into an equivalent matrix. Each row or column operation on a matrix corresponds to the corresponding operation on a system of linear equations. The block of numbers 2) above is called the augmented matrix of the system 1).

Rank of a matrix. The rank of a matrix is an important property associated with a matrix. Let A be the augmented matrix of a system of m linear equations in n unknowns. Then, intuitively, the rank of A corresponds to the number of linearly independent equations in the system. If there are four equations, but one is dependent upon the other three, then the rank of the augmented matrix A will be three. As we transform system 1) above into successively simpler systems through successive application of the three elementary operations (a), (b) and (c), we eliminate the dependent equations and end up with r linearly independent equations. Thus the rank r of the associated augmented matrix A is revealed by the time we have finished. We shall soon introduce the concepts of a linear space, linearly independent sets of vectors, subspaces spanned by sets of vectors, and the idea of the row space of a matrix. The rank of a matrix can be viewed as the dimension of the row space of the matrix i.e. as the dimension of the subspace spanned by the rows of the matrix (where the rows are viewed as vectors). Or, stated differently, it is the number of linearly independent rows that the matrix contains. The rank of a matrix can also be defined in another way. Consider the set of all possible minors of a matrix A (a minor is the determinant of any square submatrix of A — obtained by striking out rows and columns). The rank of A is the order of the largest non-zero minor of A i.e. if a matrix A has non-zero minors of order r and no non-zero minors of order r + 1, then A is of rank r.

Example. Consider the matrix

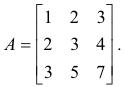
It is of rank r = 2 since

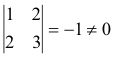
while |A| = 0.

The elementary operations for matrices. The following operations, performed on a matrix, do not change either its order or its rank.

1. Interchanging any two rows or any two columns.

2. Multiplying any row or column by a non-zero constant.

3. Adding to any row a constant times another row or adding to any column a constant times another column.

We denote the different operations as follows:

– interchange of the i-th and j-th rows

– interchange of the i-th and j-th columns

– multiplication of the i-th row by the non-zero constant k

– multiplication of the i-th column by the non-zero constant k

– addition to the i-th row the product of k times the j-th row

– addition to the i-th column the product of k times the j-th column

These operations are termed the elementary operations or elementary transformations.

Inverse operations. The inverse of an elementary operation is an operation which undoes the effect of the elementary operation. In other words, after a matrix has been subjected to one of the elementary operations and then the resulting matrix has been subjected to the inverse of that elementary operation, the final result is the original matrix.

The inverse operations are:

Thus we note that an inverse of an elementary operation is an elementary operation of the same type.

Equivalent matrices. Two mxn matrices are called equivalent if one can be obtained from the other by a sequence of elementary operations.

Equivalent matrices have the same order and the same rank.

Row equivalence. If a matrix B can be obtained from a matrix A by a finite sequence of elementary row operations it is said to be row-equivalent to A.

If matrices A and B are row-equivalent the homogeneous systems of linear equations AX = 0 and BX = 0 have exactly the same solutions.

Row Canonical Form. The row canonical form of a matrix represents the simplest form to which a matrix can be reduced by elementary row operations. If the rank of a matrix A is r then the row canonical form to which A can be reduced is called a row-reduced echelon matrix and can be described as follows:

1. Each of the first r rows will contain one or more non-zero elements while the remaining rows will consist of all zeros.

2. In each of the first r rows the first non-zero element will be a “1" and these 1's will be staggered to the right as one proceeds row-wise down the matrix (i.e. in each row the initial 1 will be at least one column to the right of the 1 in the preceding row).

3. All other elements in any column containing an initial 1 are zeros.

The following is an example of a row-reduced echelon matrix:

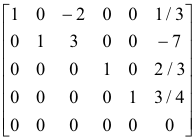
Every mxn matrix is row-equivalent to some unique row-reduced echelon matrix called its row canonical form.

Elementary row and column operations effected through multiplication by elementary matrices. The action of applying an elementary row or column operation to a matrix can also be effected by multiplying the matrix by a simple matrix called an “elementary matrix”.

Elementary matrix. An elementary matrix is the matrix that results when one applies an elementary row or column operation to the identity matrix, I_n. An elementary row matrix is the matrix obtained when one applies an elementary row operation to the identity matrix I_n. An elementary column matrix is the matrix obtained when one applies an elementary column operation to the identity matrix I_n.

The following are some examples. We are using the same symbols for the matrix as we use for the operation.

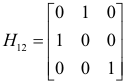
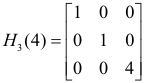
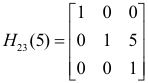
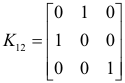
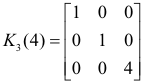
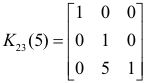
Theorem. To effect any elementary operation on a given m×n matrix A, one may first perform the same elementary operation on an identity matrix of appropriate order, then premultiply A by the result if the operation is on rows, post-multiply if it is on columns.

To effect a given elementary row operation on a m×n matrix A, apply the transformation to I_n to form the corresponding elementary row matrix H and multiply A on the left by H.

To effect a given elementary column operation on a m×n matrix A, apply the transformation to I_n to form the corresponding elementary column matrix K and multiply A on the right by K.

Thus if we wish to interchange rows 1 and 2 of matrix

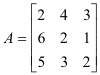
we can do it as:

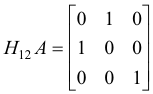
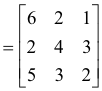
If we wish to interchange columns 1 and 2 of matrix A we can do it as

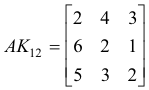
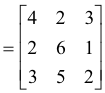
Any matrix A can be reduced to its canonical form through multiplication by a sequence of elementary matrices i.e.

H_s .... H₂H₁AK₁K₂ .... K_p = canonical form

where H₁, H₂, .... ,H_s and K₁, K₂, .... ,K_p are elementary matrices.

Note. The elementary column matrix associated with an elementary column operation is the transpose of the corresponding elementary row matrix associated with the same elementary operation on rows – and vice versa.

Theorem. If E is the elementary matrix associated with an elementary operation then its inverse E^-1 is the elementary matrix associated with the inverse of that operation.

Reduction to canonical form. Any matrix of rank r > 0 can be reduced by elementary row and column operations to a canonical form, referred to as its normal form, of one of the following four types:

where I_r is the identity matrix of order r i.e

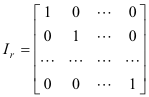
All matrices that reduce to the same normal form through elementary row and column transformations are equivalent. Two mxn matrices A and B of the same rank will reduce to the same normal form.

Theorem. Two mxn matrices A and B are equivalent if and only if they have the same rank.

Theorem. A nonsingular matrix can be reduced to normal form by row transformations alone.

Equivalent matrices. Let A and B be equivalent matrices. Let the elementary row and column matrices corresponding to the elementary row and column operations which reduce A to B be designated as H₁, H₂, ... ,H_s and K₁, K₂, ... ,K_t where H₁ corresponds to the first row operation, H₂ to the second, ...., K₁ corresponds to the first column operation, K₂ to the second, etc.. Then

H_s .... H₂H₁AK₁K₂ .... K_t = PAQ = B

where P = H_s .... H₂H₁ and Q = K₁K₂ .... K_t

Theorem. Two mxn matrices A and B are equivalent if and only if there exist nonsingular matrices P and Q such that B = PAQ.

Inverse of a product of elementary matrices. Let P and Q be the product of elementary matrices

P = H_s ... H₂•H₁ and Q = K₁ ... K₂•K_t

Since each H and K has an inverse and since the inverse of a product is the product in reverse order of the inverses of the factors

Let A be an n-square non-singular matrix and let P and Q defined above be such that PAQ = I_n. Then

3) A = P^-1(PAQ)Q^-1 = P^-1•I_n•Q^-1 = P^-1•Q^-1

We have thus proved

Theorem. Every non-singular matrix can be expressed as a product of elementary matrices.

Canonical set under equivalence. Any mxn matrix is equivalent to a mxn canonical matrix of one of the following normal types

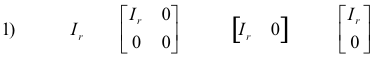
A set of mxn canonical matrices to which any mxn matrix is equivalent is called a canonical set. For example, a canonical set for all non-zero 3x4 matrices is the set:

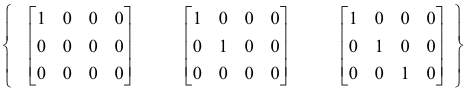
This set represents the set of normal forms of rank 1, 2 and 3. Any non-zero 3x4 matrix can be reduced by elementary operations to one of the members of this canonical set. In general, a canonical set for all matrices of dimension mxn is a set of normal forms of type 1) above where the rank r ranges over the values 1, 2, ...., m or 1, 2, ...., n whichever is smaller.

Theorems.

1] Two mxn matrices A and B are equivalent if and only if there exist nonsingular matrices P and Q such that B = PAQ.

2] If A is a square nonsingular matrix, there exist nonsingular matrices P and Q such that PAQ = I.

3] Every nonsingular matrix can be expressed as a product of elementary matrices.

4] If a matrix A is nonsingular, the rank of AB (also of BA) is that of B.

5] If P and Q are nonsingular, the rank of PAQ is that of A.

6] The rank of the product of two matrices cannot exceed the rank of either factor.

7] If the mxp matrix A is of rank r and if the pxn matrix B is such that AB = 0 the rank of B cannot exceed p-r.

References.

Ayres. Matrices (Schaum).