Website owner: James Miller
Prism spectroscope. Emission and absorption spectra. Continuous, line, and band spectra. Fraunhofer lines. Bohr theory of the hydrogen atom.


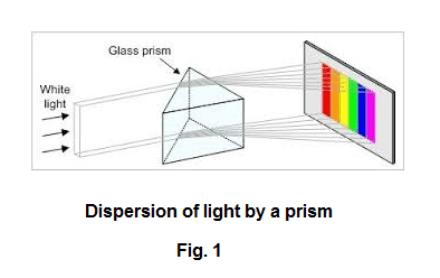
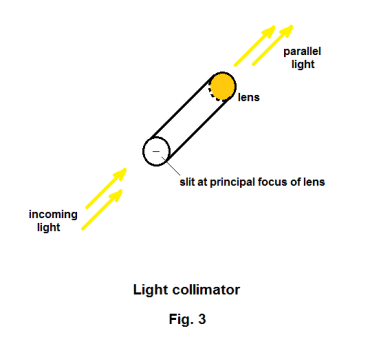
The spectroscope. If one passes a beam of sunlight through a prism as shown in Fig. 1, light of different wavelengths will be refracted by different amounts with the consequence that a spectrum of different colors will be obtained. A spectroscope is a device used to examine the spectra of light from different sources. A picture of a prism spectroscope is shown in Fig. 2. A prism spectroscope consists of three things: 1) a collimator, 2) a prism, and 3) a small telescope. A collimator is a tube with a lens at one end and a small slit at the other end where the distance from the slit to the lens is equal to the focal length of the lens i.e. the slit is located on the principal focus of the lens. Light entering the slit emerges from the lens as a beam of parallel light rays. See Fig. 3. Thus the function of the collimator is to produce a beam of light whose rays are parallel. The source of the light to be examined is placed at the slit and the parallel light emanating from the collimator is passed through the prism giving rise to a spectrum. The telescope magnifies the spectrum and allows viewing. Crosshairs in the telescope can be focused on any line in the spectrum. The collimator and the telescope are mounted on a circular protractor so that the angular position of any line can be measured.
When a spectroscope is fitted for making precise measurements of spectra, it is called a spectrometer. When it is fitted for photographing spectra, it is called a spectrograph.
Light and spectra. The light that is emitted by a particular light source may consist of one wavelength only (monochromatic light), it may consist of several discrete wavelengths, or it may, like sunlight, consist of an unbroken band of wavelengths within some interval. If the light consists of several discrete wavelengths, its spectrum will consists of several lines with each line corresponding to one of the constituent wavelengths.
Let us dip a platinum wire into a solution of common table salt (sodium chloride), and then hold the wire in the colorless flame of a Bunsen burner. A bright yellow light will be produced by the vaporization of the salt. If this bright yellow light is passed through a collimator and then through a prism, a spectrum consisting of two bright-yellow lines, spaced very close together, will be seen. These two spectral lines represent the two wavelengths that compose the light. Spectra consisting of a number of distinct lines are called line spectra.
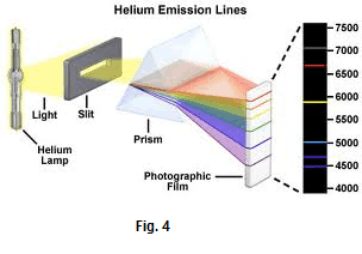
Fig. 4 shows the line spectrum associated with helium. Each line represents an image of the slit. Fig. 5 shows the spectra of several kinds of gas.
Luminous gases or vapors under atmospheric pressure produce bright-line spectra. A line spectrum consists of distinct and separate colored lines.
Absorption spectra. Let us hold a platinum wire in the colorless flame of a burner until it is incandescent. The spectrum produced is a continuous one, an unbroken band of seven colors. Now let us place between the slit and the prism a pan containing a solution of salt water and let us heat it enough to vaporize the sodium chloride, creating a sodium chloride vapor, as shown in
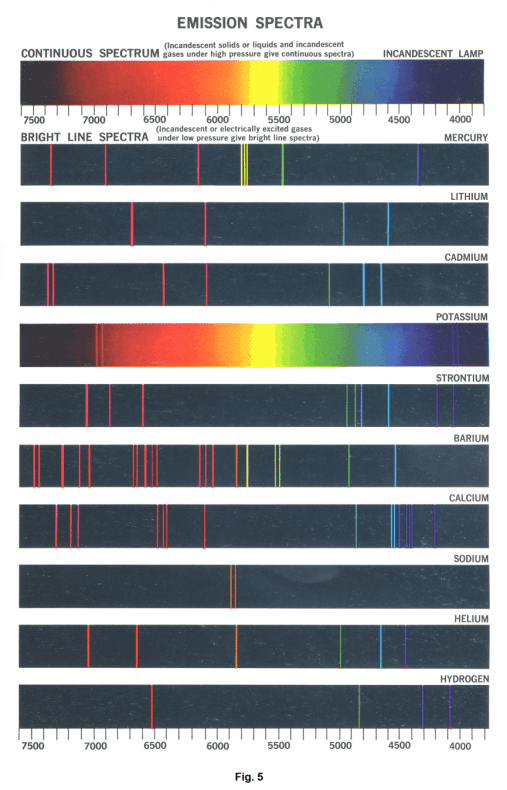
Fig. 6. When we do this, two dark lines will appear in the platinum wire spectrum just where the
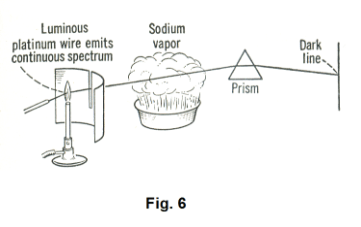
two lines of the sodium bright-line spectrum are located. The explanation for this phenomenon? The sodium chloride vapor has absorbed those two wavelengths from the platinum wire spectrum.
An absorption spectrum is a continuous spectrum interrupted by dark lines. The dark lines are produced by the above mechanism. Gases or vapors can absorb light waves of the same length that they would produce themselves if they were heated to incandescence.
Types of spectra. Every luminous substance emits a characteristic spectrum, a spectrum unique to it. The same substance may produce different spectra when excited to luminosity by different means.
Spectra can be divided into two general types:
1) Emission spectra
2) Absorption spectra
Emission spectra can be divided into three types:
1) Continuous spectra
2) Line spectra
3) Band spectra
Band spectra. Some emission spectra appear as fluted bands of color rather than as sharply defined lines. Such spectra are called band spectra. These bands consist of groups of lines so close together that they are not easily resolved.
Production of continuous spectra. Any incandescent solid or liquid will produce a continuous spectrum (an unbroken band of seven colors). In addition, gases under extremely high pressure will produce a continuous spectrum.
Production of line spectra. In general, line spectra are produced by introducing a volatile salt into a flame, passing electricity through a gas, vaporizing a metal in an electric arc, etc.
Three laws of spectroscopy:
1. An incandescent solid, liquid or gas under high pressure emits a continuous spectrum.
2. A hot gas under low pressure emits a "bright-line" spectrum.
3. Radiation from a continuous spectrum source passing through a cool, low-density gas produces an absorption-line spectrum.
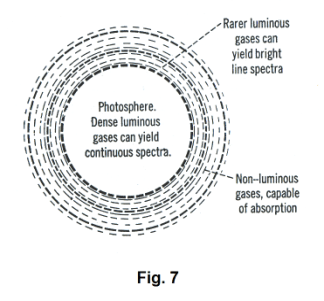
The Fraunhofer lines. In 1802 the English scientist William Hyde Wollaston noticed that there were some dark lines in the solar spectrum. About ten years later they were also discovered by the German physicist Joseph von Fraunhofer. With apparatus that he had constructed himself, Fraunhofer charted the positions of approximately 600 of these dark lines and observed that they always appear in the same positions in the spectrum. In addition, their positions are the same as those occupied by the bright lines in the spectra of the luminous vapors of certain elements. These dark lines are called Fraunhofer lines.
We thus see that the sun produces an absorption spectrum. How it might do this can be explained by examination of Fig. 7. The photosphere consists of highly compressed gases that would give a continuous spectrum. The next layer out, the chromosphere, consists of luminous gases under less pressure which, alone, would form bright-line spectra. In the outer layers of the sun, and to a lesser degree, in the earth’s atmosphere, are nonluminous gases which absorb specific wavelengths and produce the dark lines seen in the spectrum.

The basic mechanism by which light is produced. Light. What is it? Where does it come from? How is it produced? We know that the sun and incandescent materials give out light. But how is it produced at a deeper level? These were questions that were surely asked by scientific investigators back in the 1800's. It was natural for them look for some mechanism at the level of the atom to explain the phenomenon of light. Hydrogen, because it is the simplest of the elements, was studied much in those days. Fig. 8 shows the emission spectrum of hydrogen in the visible and near ultraviolet range. Johann Balmer, in 1885, found a simple formula that gave this sequence of wavelengths:
1) 1/λ = R(1/22 - 1/n2) n = 3, 4, 5, ...
where λ is the wavelength and R is a constant called the Rydberg constant. If λ is in meters, R = 1.097 × 107 m-1 (i.e. 1/1.097 × 107 m). Evaluation of this formula for n = 3, 4, 5, ... gives the values Hα = 656.3 mμ, Hβ = 486.1 mμ, etc.
The series given by 1) is called the Balmer series. As n approaches infinity, the lines crowd together and the series approaches a limit called the series limit, H∞.
Three other series for hydrogen have since been found:
Lyman series: 1/λ = R(1/12 - 1/n2) n = 2, 3, 4, ...
Paschen series: 1/λ = R(1/32 - 1/n2) n = 4, 5, 6, ...
Brackett series: 1/λ = R(1/42 - 1/n2) n = 5, 6, 7, ...
The Lyman series is in the ultraviolet, and the Paschen and Brachett series are in the infrared. Examination of the formulas shows that the Balmer series fits in between the Lyman and Paschen series.
Utilizing the fact that
c = fλ or, 1/λ = f/c
we can write the Balmer formula 1) as
2) f = Rc (1/22 - 1/n2) n = 3, 4, 5, ...
or
3) f = Rc/22 - Rc/n2
The Bohr theory on light production. In 1913 Niels Bohr proposed a theory on how light was produced. In his theory light was produced by electrons in an atom jumping from a higher energy-level orbit to a lower energy-level orbit, giving off energy in the form of light as they made the jump. His theory, as applied to the hydrogen atom, with certain basic assumptions on how things worked inside an atom, gave frequencies for the emitted light that corresponded exactly to the frequencies of the Balmer series.
Experiments performed by Rutherford on the scattering of alpha-particles by thin metallic foils around 1906 led researchers to the belief that atoms consisted of a relatively massive, positively charged nucleus, surrounded by a swarm of relatively light, negatively charged particles (electrons). To account for the fact that the electrons remained at relatively large distances from the nucleus in spite of the electrostatic force of attraction of the nucleus for them, Rutherford hypothesized that the electrons revolved in orbits about the nucleus with the force of attraction providing the centripetal force needed to keep them in their orbits. There was, however, a problem with this model. A particle moving in an orbit about a point is continually being accelerated toward that point and according to electromagnetic theory, a charged particle that is being accelerated radiates electromagnetic radiation. Thus if the theory were true, the electrons in matter would be continually radiating electromagnetic energy. In addition, as they radiated energy, their kinetic energy would gradually decrease, their orbits would become smaller and smaller, and they would eventually spiral into the nucleus and come to rest.
Bohr was attempting to devise a model for the workings within an atom that would explain the line spectrum produced by hydrogen. The model he proposed made three assumptions:
1] Electrons can and do orbit nuclei without emitting electromagnetic energy.
2] The orbits in which the electrons orbit the nucleus are restricted to those orbits for which the angular momentum mvr is some multiple of h/2π, or equivalently,
3) 2π mvr = nh
where
m = mass of an electron
v = velocity of the electron
r = radius of the orbit
h = Planck’s constant
n = integer 1, 2, 3, ... corresponding to the number of the orbit
3] If an electron jumps from an orbit of energy level E1 to an orbit of energy level E2, a photon of energy hf = E1 - E2 is emitted or absorbed (emitted if it moves from a higher energy orbit to a lower energy orbit or absorbed if it moves from a lower energy orbit to a higher energy orbit).
Quantum theory. A theory that asserts that radiant energy of frequency f can only be emitted or absorbed in discrete amounts that are integer multiples of hf, where h is Planck’s constant. Each package or quantum of energy is given by
4) E = hf
where E is the energy of the quantum in joules.
Def. Photon. A photon is a quantum of electromagnetic energy.
Thus a photon (or quantum) of blue light contains more energy than a photon of red light because blue light has a shorter wavelength and thus higher frequency than red light.
Derivation of the total energy of an electron orbiting in Orbit n. The total energy E of an electron orbiting in Orbit n is the sum of its kinetic energy Ek and it potential energy Ep
5) E = Ek + Ep
The hydrogen atom consists of a single electron of charge -e rotating about a single proton of charge +e. The centripetal force holding the electron in orbit is given by
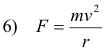
This force is provided by the force of attraction between the electron and proton which is given by
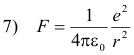
Thus, equating 6) and 7)
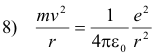
Solving equations 8) and 3) for r and v we obtain
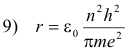
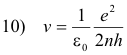
Let
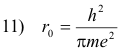
Then 9) becomes
12) r = n2r0
and the permitted orbits are of radii
r0, 4r0, 9r0, ...
The number n is called the quantum number of the orbit.
The values of ε0, h, m, and e are
ε0 = 8.85 × 10-12 coul2/newton∙m2
h = 6.62 × 10-34 joule-sec
m = 9.11 × 10-31 kg
e = 1.60 × 10-19 coul
Evaluating r0 from11) gives
13) r0 = 0.53 × 10-8 cm
which agrees well with atomic diameters as estimated by other methods.
The kinetic energy Ek of the electron in any orbit n is
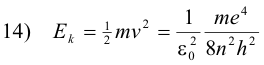
The potential energy of the electron is the work required to bring a unit negative charge from infinity (the conventionally accepted zero reference) to a distance r from the nucleus and is given by the formula
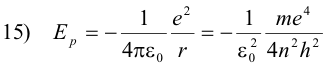
Because it is a negative charge that we are bringing in from infinity, the work required is negative and consequently the potential energy is negative (if we were bringing in a positive charge, the work would be positive because of repulsion). However, because we are only interested in energy differences, this is not of importance.
The total energy E of the electron is then
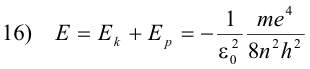
The orbit of least energy is the orbit for which n = 1, since this is the orbit for which E has the largest negative value. One must remember that one does work on a negative charge (i.e. an electron) in carrying it from an inner orbit to an orbit further out, thus giving it a greater potential energy for orbits further away from the nucleus.
The normal state of the atom is that of lowest energy, with the electron revolving in the orbit of smallest radius, r0. As a result of collisions with rapidly moving electrons in an electrical discharge, or due to some other cause, an atom may temporarily acquire enough energy to cause the electron to jump to some outer orbit, in which case the atom is said to be in an excited state. This state is an unstable one, and the electron soon falls (or “jumps”) back to a state of lower energy, emitting a photon in the process.
Let n be the quantum number of some excited state, and l the quantum number of the lower state to which the electron returns after the emission process. Then the energy of the atom in the excited state is
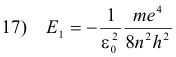
and its energy in the lower state is
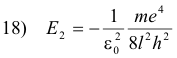
The decrease in energy, E1 - E2, is equal to the energy hf of the emitted photon
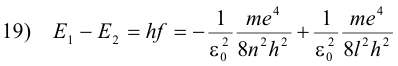
or
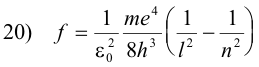
Note that if we place
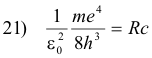
this equation has exactly the same form as the Balmer series 2) above:
2) f = Rc (1/22 - 1/n2)n = 3, 4, 5, ...
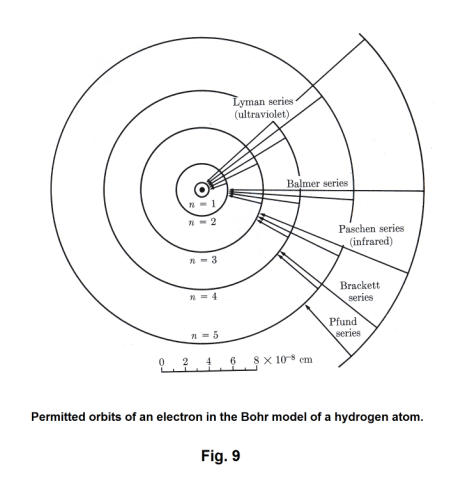
Letting l = 1 in 20), we obtain the Lyman series, letting l = 2, we get the Balmer series, etc. The Lyman series is thus the group of lines emitted by electrons returning from some excited state to the normal state. The Balmer series is the group emitted by electrons dropping from some higher state to the second orbit instead of falling all at once to the first orbit. In other words, an electron dropping from the third orbit to the second orbit emits the Hα line, an electron dropping from the fourth orbit to the second orbit emits the Hβ line, etc. See Fig. 9.
Is the statement represented by eq. 21) true? The values of all the constants in it are derived independently. Does the equality hold? Yes it holds exactly, within the limits of experimental error.
References
1. Dull, Metcalfe, Brooks. Modern Physics.
2. Sears, Zemansky. University Physics.
3. Semat, Katz. Physics.
4. Schaum. College Physics.
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life