Magnetic field of a moving charge. Electromagnets. Magnetic field intensity H and magnetic induction B. Magnetic field of a long straight wire, circular coil, solenoid, toroid, and moving charge. Permeability.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Magnetic field of a moving charge. Electromagnets. Magnetic field intensity B. Magnetic field of a long straight wire, circular coil, solenoid, toroid, and moving charge. Permeability.

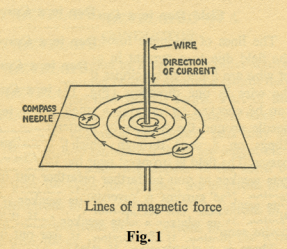
Magnetic field of a moving charge. Up until 1819 there was not known to be any connection between electrical and magnetic phenomena. They were studied separately and assumed to be unrelated. In 1819 Danish scientist Hans Christian Oersted observed that a compass needle was deflected when near a wire carrying electric current. In fact, a wire carrying a current generates a magnetic field in the space around it of the sort shown in Figures 1 and 2. The figures show magnetic flux lines encircling a current-carrying wire. The field continues out indefinitely into space.

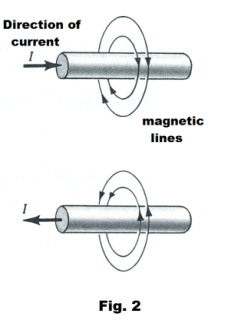
Right-hand rule for determining the direction of the field. Point the thumb of the right hand in the direction of the current and the curled fingers will point in the direction of the magnetic lines.

Is this phenomenon restricted to conductors carrying current or does any moving charge produce a magnetic field? Experiments have confirmed that any moving charge produces a magnetic field. As a consequence, a beam of electrons in a cathode ray tube will generate a magnetic field similar to that produced by a current in a wire. Electrons create magnetic fields as they orbit nuclei and as they spin about their own axes.

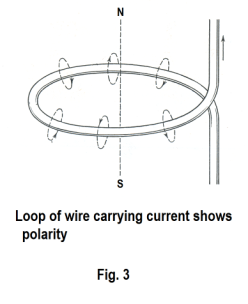
Magnetic field of a solenoid. Consider current flowing through a loop as shown in Fig. 3. Examination of the figure shows that the magnetic field generated by the flow of current through a loop of wire shows polarity. Inside the loop all the magnetic lines are pointed upward making the top a north seeking pole. Now let us add more loops. See Fig. 4.

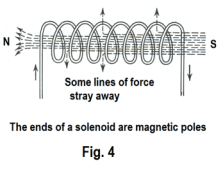
Each loop becomes a magnet, and the whole spiral acts like a pile of disc magnets with their unlike poles adjacent. Such a tube-shaped coil of (insulated) wire is called a solenoid. A solenoid is analogous to a bar magnet. It has a pole at each end and the polarity is reversed if the current is reversed.

In Fig. 4 we see that much of the magnetic flux escapes out between the coils of the solenoid, a phenomenon that weakens the strength of the solenoid considerably. We can prevent this by placing a bar of soft iron or silicon steel inside the solenoid. The flux now stays strictly within the bar, greatly increasing the strength of the solenoid. A core of a ferromagnetic material such as soft iron or silicon steel will increase the strength of a solenoid by thousands of times, due to the high permeability μ of the material.

Right-hand rule for finding direction of the magnetic field in a solenoid: If the fingers of the right hand are wrapped around the coil in the direction of current flow, the thumb will point in the direction of the flux lines.

The north pole of the solenoid is the end where the flux lines emerge.

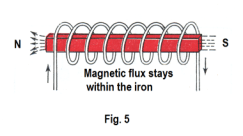
The electromagnet. A solenoid with an iron core is an electromagnet. The electromagnet was invented in 1824 by British scientist, William Sturgeon. The strength of an electromagnet depends on the number of turns and on the strength of the current. An electromagnet is a magnet only when current is flowing. When the current is turned off it loses all its magnetism (except for a trace of residual magnetism in the core).

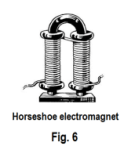
Permanent magnets are often made in the shape of a horseshoe to bring the poles closer together and thus increase the intensity of the magnetic field. One can do the same thing with electromagnets. Fig. 6 shows a horseshoe electromagnet. The wire is wound around one pole in one direction and the other pole in the opposite direction.

Uses of electromagnets. Electromagnets are used in many places. Powerful electromagnets

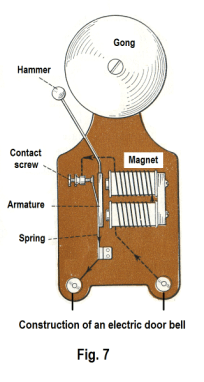
that can lift several tons are used to move scrap iron. Surgeons use electromagnets to remove steel splinters from a person’s eyeball or other parts of his body. Many electrical instruments such as the electric door bell, the telegraph, the telephone, the electric generator, and the electric motor use electromagnets. Fig. 7 shows the construction of an electric door bell operated by a horseshoe magnet.

Magnetic field intensity B at a point P in a magnetic field. The force that would be exerted on a unit north pole if it were placed at the point.

The magnetic field intensity is a vector pointed in the direction of the magnetic field at point P with a magnitude given as the force that the field would exert on a unit pole.

The magnetic field intensity B is a measure of flux density at a point. Given a point P in some magnetic field R, let us pass a plane D through P perpendicular to the direction of the magnetic field at point P. Then the magnetic field intensity B at P is a measure of the flux density at P. It can be viewed as so many lines of force per unit area (i.e. lines per sq. meter) passing perpendicularly through plane D at point P.

The magnetic field intensity B is also called magnetic induction B. It has units of webers/m².

Def. Weber. The weber is the magnetic flux which, linking a circuit of one turn, would produce in it an electromotive force of 1 volt if it were reduced to zero at a uniform rate in 1 second.

Magnetic field strength H. The magnetic field strength H is a measure of field strength related to B by

1) B = μH

where μ is the permeability of the medium. The mks unit of magnetic field strength H is the ampere-turn/m.

Permeability of a vacuum. The permeability a vacuum is given by:

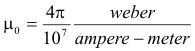
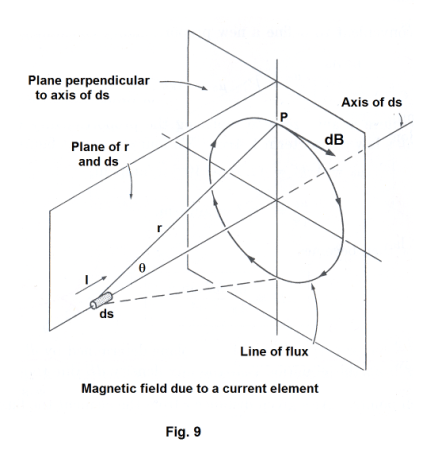
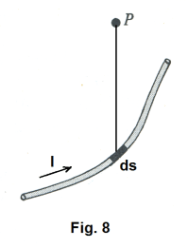
Magnetic field of a current element. Let ds be a differential increment of a wire carrying a current I. See Fig. 8. The current in the wire generates a magnetic field in the space around it. Each differential increment ds of the wire can be viewed as making its own individual contribution to the total magnetic field intensity B at any specified point P in space. The contribution that a differential element ds makes to the magnetic field intensity B at point P is given by the cross product

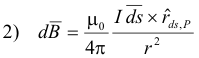
where r is the distance from ds to P, and is a unit vector directed from ds to P (bold type and over-bar both used to indicate vector). In non-vector form, this formula is

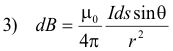
where θ is the angle between the direction of ds and the line from ds to P shown in Fig. 9. The vector dB is perpendicular to the plane of r and ds as shown in the figure. Equation 2) is sometimes called the Biot law and also often called Ampere’s law.

The total magnetic field intensity B at a point P arising from a particular circuit is found by summing vectorially the contributions dB from all the elements ds of the circuit i.e.

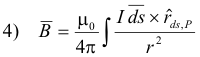
For most circuit configurations, this problem is beyond the methods of calculus and must be done using numerical methods of integration.

Magnetic field of a long straight wire. The magnetic field intensity B at a perpendicular distance a from the axis of a long straight wire carrying a current I is

Proof

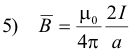
Magnetic field of a flat circular coil. The magnetic field intensity B at the center of a flat circular loop of wire of radius r carrying current I is given by

Proof

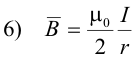
For a closely wound flat circular coil of n turns, the magnetic field intensity B at the center is given by

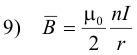
Magnetic field B of a solenoid and toroid. At any point on or near the axis of a solenoid not too near either end, the magnetic field intensity B is given by

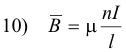
where n is the number of turns, l is the length, I is the current, and μ is the permeability of the material making up the core. For a vacuum (or air) core, μ = μ₀.

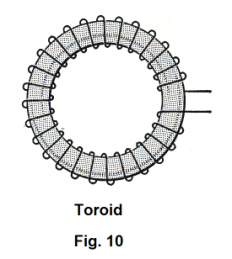
A toroid is made by winding wire on a ring or doughnut shaped form called a torus. See Fig. 10. The field of a toroid is completely confined to the space within the toroid. A toroid can be viewed as a solenoid that has been bent into the form of a ring. The magnetic field within a toroid is given by formula 10), where l now represents the mean circumference of the ring.

The solenoid and toroid are often used as a means of achieving known, uniform magnetic fields.

Permeability. If the core of a solenoid or toroid is a magnetic material such as soft iron instead of a vacuum, the magnetic induction B is increased tremendously. Thus the magnetic induction B of a solenoid or toroid is dependent not only on nI/l, but also on the properties of the material in the core.

Let B represent the flux density in a toroid with a material core and B₀ the flux density in a toroid with a vacuum core. The ratio of B to B₀ is called the relative permeability of the material and is represented by μ_r

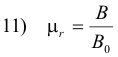
The relative permeability μ_r is

● equal to 1 for a vacuum

● slightly larger than 1 for paramagnetic materials

● slightly smaller than 1 for diamagnetic materials

● often much larger than 1 for ferromagnetic materials

From 10) we have

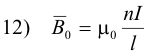
From 11) and 12) we have

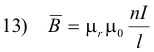
where μ₀ is the permeability of a vacuum:

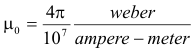
The product μ_rμ₀ is called the permeability of the material and is denoted by μ:

14) μ = μ_rμ₀

The permeability μ is

● equal to μ₀ for a vacuum

● slightly larger than μ₀ for paramagnetic materials

● slightly smaller than μ₀ for diamagnetic materials

● often much larger than μ₀ for ferromagnetic materials

The expression for the flux density B in a toroid with a material core can now be written as

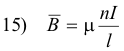
Theorem 1. Let ds be a differential increment of a wire carrying a current I with dq being the quantity of charge that passes a complete cross-section of wire in time dt. Then

16) I ds = v dq

i.e. a charge dq moving with velocity v is equivalent to a current element of length ds carrying a current I.

Proof. I = dq/dt and ds = v dt. Eliminating dt from these two equations gives I ds = v dt

Magnetic field B of a moving charge. The magnetic field B at a point P due to a charge q moving with velocity v is given by

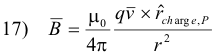
where r is the distance from the charge to point P and is a unit vector from the charge to point P.

Proof. Using I ds = v dq from Theorem 1 and substituting into eq. 2) above gives

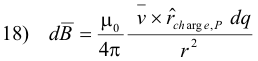
Integrating 18) gives 17).

References

1. Dull, Metcalfe, Brooks. Modern Physics.

2. Sears, Zemansky. University Physics

3. Semat, Katz. Physics.