Website owner: James Miller
Electrostatics. Electrical potential energy. Potential. Potential difference. Volt. Equipotential surfaces. Potential gradient. Ice pail experiment.
Electrical potential energy. If we lift a 50 lb body 500 ft above the surface of the earth, the process can be viewed as doing work to separate two parts of a system that attract each other. The work done in separating the body from the earth increases the gravitational potential energy of the body-earth system, and when the body is allowed to fall, the two parts of the system come together again and the potential energy is released. The same ideas can be applied to any system composed of bodies that attract each other. The attraction doesn’t need to be gravitational. Work must be done to separate a positive charge from a negative charge, and this work can be recovered when the two charges are allowed to approach each other. Unlike gravitational forces, which are always attractive, the electrical forces between charges can be either attractive or repulsive, depending on whether the charges are unlike or like.
The law of universal gravitation is
![]()
The law of attraction between two unlike charges is
![]()
We note the form is the same. The gravitational field is a conservative force field. The electric field of a point charge is also a conservative force field.
Work required to move a test charge from point a to point b in any arbitrary electrical field. The work required to move a small positive test charge qʹ from point a to point b in an arbitrary electrical field E (i.e. a field created by any arbitrary distribution of charges) is
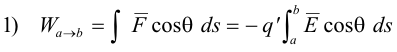
where the force acting on the charge is F = -qʹ E and θ is the angle between F (or E) and the direction of travel ds.
Work required to move a test charge from point a to point b in the field of a point charge. Let us now apply formula 1) above to the case of a field produced by a single point charge q. In this case
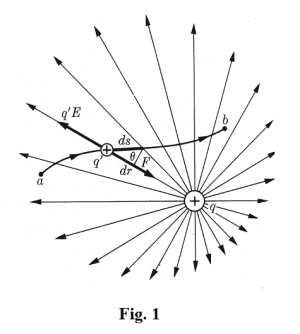
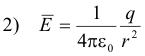
3) ds cos θ = dr
See Fig. 1. Substituting 2) and 3) into 1), we get
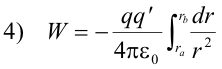
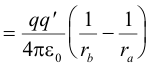
or
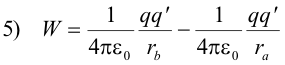
where ra is the distance of point a from the point charge and rb is the distance of point b from the point charge.
Examination of formula 5) shows that in the field of a single point charge q, the work required to move a test charge from a start point a to an end point b depends only on the initial and final distances of the points a and b from the charge q. This means that the work is the same for any path between these two points (or between any pair of points at the distances ra and rb from the point charge). It also means that if the test charge is returned from point b to point a along any path, the work done to move it can be completely recovered. Thus the electric force is a conservative force and we are justified in considering the work done on the test charge as an increase in its potential energy.
Potential energy of a test charge in a point charge field. If in formula 5), ra = ∞ and rb = r, the formula gives us
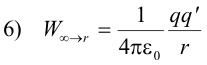
as the amount of work done in bringing a test charge q' from infinity to a point located at a distance r from point charge q. We define the potential energy (P.E.) of a test charge qʹ located at a distance r from a point charge q as
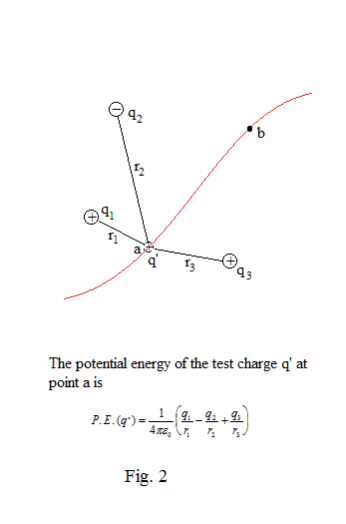
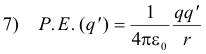
Potential energy of a test charge in a general electric field. Let us derive an expression for the potential energy of a test charge in an electric field arising from some arbitrary distribution of charges. An arbitrary charge distribution can always be viewed as a collection of individual point charges q1, q2, q3, ... . Let us suppose that the arbitrary charge distribution consists of the individual point charges q1, q2, q3, ... which are located at distances r1, r2, r3, ... from a test charge qʹ . The total potential of the test charge qʹ at point a is the sum of its potential energies with respect to all of the charges (i.e. all charges other than the test charge itself) in the field.
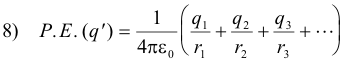
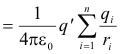
See Fig. 2 (Note that the sign of the charges can be either plus or minus.) The potential energy of qʹ at some other point b will be given by the same formula except that r1, r2, r3, ... will refer to the distances from point b to the various charges. The work necessary to move the test charge from point a to point b along any path is equal to the difference between its potential energies at point a and point b. Thus
![]()
Consequently we see that we can compute the work required to move a small positive test charge qʹ from point a to point b in an electrical field E either by using the formula
![]()
or by computing the potential energies at points a and b and subtracting one from the other.
It will be seen from equation 8) that the potential energy of a test charge located at an infinite distance from all the charges of a charge distribution (in which case all distances r1, r2, r3, ... are infinite) will be zero. The potential energy of a point at infinity is used as a reference level for electrostatic potential energy. Consequently we have: The potential energy of a test charge at any point a is equal to the amount of work required to bring the test charge from infinity to the point a.
Def. Potential. The ratio of the potential energy of a test charge at a point to the magnitude of the charge i.e. the potential energy per unit charge.
Denoting the potential at point a by Va we have
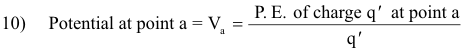
It follows that
11) P.E. of charge qʹ at point a = qʹVa
The above definition of potential is analogous to the definition of the electric intensity at a point as force per unit charge. The potential at a point is considered to have a value even though there may be no charge at the point. We imagine placing a test charge at the point and then compute its potential energy and take the ratio of its potential energy to charge.
The reference level for potential in electrostatics is a point at infinity. The potential of a point at infinity is zero. All potentials can be viewed as potential differences referenced, or compared to, the potential of a point at infinity.
Def. Volt. The volt is the unit of potential in the MKS system. One volt is equal to one joule per coulomb. The volt can be defined by either of the following definitions:
1] The potential at a point in an electrostatic field is one volt if one joule of work per coulomb is done against electrical forces when a charge is brought from infinity to the point.
2] The potential at a point in an electrostatic field is one volt if the ratio of the potential energy of a charge at the point, to the magnitude of the charge, is one joule per coulomb.
Volt units
- one one-thousandths of a volt is called a millivolt (mv)
- one millionth of a volt is called a microvolt (μv)
- one thousand volts is a kilovolt (kV)
- one million volts is a megavolt (Mv)
Potential in an electric field produced by a point charge. Given an electric field produced by a single point charge, the potential at a point located at a distance r from the charge is
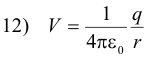
The potential is in volts if q is in coulombs and r is in meters. The distance r is always considered positive. The charge q may be positive or negative. The potential will have the same sign as the charge q.
Potential in a general electric field. Given an electric field arising from some arbitrary distribution of point charges q1, q2, q3, ... , the potential Va at a point a within the field is given by
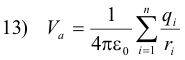
where ri is the distance from point a to point charge qi.
If the charge creating the field is distributed along a line, over a surface, or throughout a volume, we can subdivide it into infinitesimal elements dq and obtain the sum by the methods of integral calculus. Thus
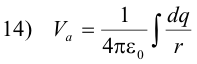
Potential difference. The difference between the potential at two points in an electrostatic field is called the potential difference between the points. Point b is said to be at higher potential than point a if work is done against electrical forces when a positive charge is moved from a to b. In other words, point b is at a higher potential than point a if the potential energy of a positive charge is greater at b than at a.
The potential difference between two points expressed in terms of electrical intensity E. The following formula for the potential difference between two points follows directly from 9) and 11) above:
![]()
where θ is the angle between E and ds.
Work done in transferring a charge q from one point to another through a potential difference of Vab .
W (joules) = q (coulombs) × Vab (volts)
where W is the work done.
Instruments for measuring potential difference. Differences of potential may be measured by electroscopes, electrometers, and voltmeters. The voltmeter is a current-operated device and isn’t suitable for electrostatic work. Because there is no simple relation between the divergence of the leaves of an electroscope and the potential difference, the electroscope is rarely used for quantitative work. For quantitative work some form of electrometer is usually used.
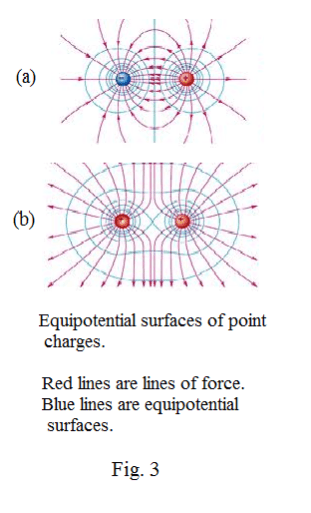
Equipotential surfaces. An equipotential surface is a surface at all points of which the potential has the same value. Fig. 3 shows slices of the equipotential surfaces associated with two unlike charges and two like charges.
Because the potential energy of a charged body is the same at all points of a particular equipotential surface, it follows that no work is done in moving a charged body over such as surface. As a consequence the equipotential surface passing through any point must be at right angles to the direction of the electric field at that point. If this were not so, the field would have a component lying in the surface and work would have to be done against the field to move a charge in the direction of this component. Thus the lines of force and the equipotential surfaces form a mutually perpendicular network.
On a charged conductor in which the charges are at rest (electrostatic situation) the lines of force at the surface are perpendicular to the surface. Thus the surface of such a conductor is an equipotential surface. Furthermore, since the field within a charged conductor is zero, the entire interior of the conductor is an equipotential volume, at the same potential as the surface.
Potential gradient. The work done in giving a small test charge qʹ a displacement ds at some point P in an electric field E is given by
![]()
![]()
Since
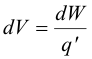
we obtain
![]()
or
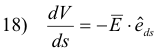
This equation represents the directional derivative at point P of the potential function V(x, y, z), giving the rate of change of the potential at point P in the direction specified by the unit vector. The rate of change of the potential is greatest for a direction perpendicular to that equipotential surface running through point P. This occurs when the unit vector is pointed in the same direction as the field vector E (i.e. direction of the lines of force). In this case the equation becomes
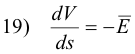
The rate of change in the direction of most rapid change is called the potential gradient. The potential gradient is the gradient of the potential function V(x, y, z). For more information on the gradient and directional derivative see Gradient, Del Operator, Directional derivative.
Sharing of charge by conductors. When a charged conductor makes contact with the external surface of one that is uncharged, the original charge flows into the uncharged conductor until both conductors are at the same potential, much as heat flows from a hot object into a cooler one until both are at the same temperature, or as water flows from a higher level to a lower one until all is at the same level. This behavior would be expected due to repulsive action of like charges. The charged conductor loses charge and the uncharged conductor gains charge until equilibrium is reached, but the charged conductor always retains some charge. If, however, a charged conductor, instead of making contact with the external surface of an uncharged conductor, makes contact with the interior surface of a hollow uncharged conductor, what occurs is quite different as is shown by the following experiment by Faraday.
Ice pail experiment. Faraday's description of the experiment, from a letter he wrote on February 4, 1843 to Richard Phillips, the editor of Philosophical Journal, and published in the March 1844 issue is:
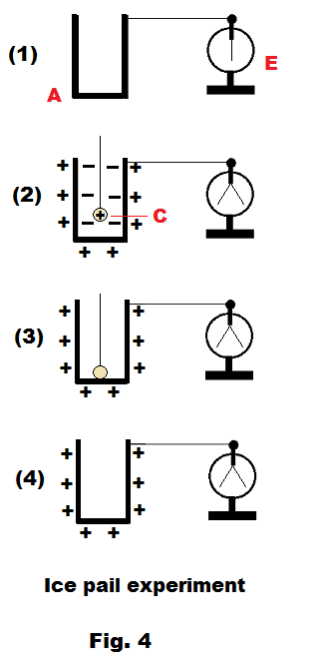
Let A in the diagram represent an insulated pewter ice-pail...connected by a wire to a delicate gold-leaf electrometer E, and let C be a round brass ball insulated by a dry thread of white silk, three or four feet in length, so as to remove the influence of the hand holding it from the ice-pail below. Let A be perfectly discharged, and then let C be charged at a distance by a [electrostatic] machine or Leyden jar, and introduced into A.. If C be positive, E will also diverge positively; if C be taken away, E will collapse perfectly... As C enters the vessel A the divergence of E will increase until C is ... below the edge of the vessel, and will remain quite steady and unchanged for any greater depression. This shows that at that distance the inductive action of C is entirely exerted upon the interior of A, ... If C is made to touch the bottom of A, all of its charge is communicated to A, ... and C, upon being withdrawn, ... is found to be perfectly discharged."
In other words, a charged brass ball is lowered into an uncharged metal ice pail whose outer surface is connected to an electroscope. As the ball is lowered into the pail, the leaves of the electroscope diverge, registering a charge. The ball is allowed to touch the bottom of the pail and then is withdrawn. The electrometer continues to register a charge, and when the ball is withdrawn, it is tested and found to have no charge. The entire charge on the ball was evidently transferred to the pail when it was allowed to make contact with the bottom of the pail.
What happened? When the charged ball was lowered into the pail, the leaves of the electroscope diverged, indicating that the exterior surface of the pail had become positively charged by induction i.e. the positively charged ball had attracted free electrons to the inner surface of the pail, leaving the outer surface of the pail and the electroscope positively charged. See Fig. 4 (2). When the ball was allowed to touch the bottom of the pail [Fig. 4 (3) ], the positive charge on the ball was neutralized by the equal and opposite charge on the inner surface of the pail. (The pail and ball acted like a single conductor and the entire excess charge went to the exterior surface of the pail.)
In this experiment, the ball after being removed from the pail, can be recharged, lowered into the pail again, allowed to touch the bottom, and that charge will also be transferred to the pail. Thus the process can be repeated, adding more and more charge to the pail.
We see here, then, a situation in which the entire charge on one conductor was transferred to another conductor — in contrast to the situation when the charge on one spreads out evenly on both.
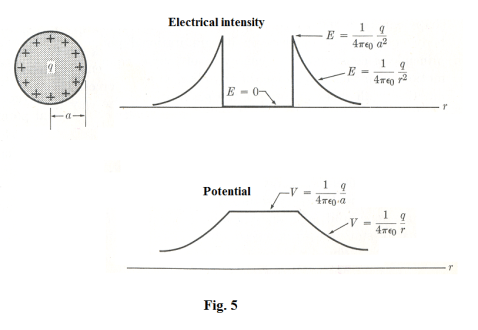
Potential of a charged spherical conductor. The electric field outside a charged spherical conductor of a total charge q is the same as that created by a point charge with charge q (i.e. it is the same as if all of the sphere’s charge were concentrated at its center). As a consequence, the potential for points outside a charged spherical conductor is given by the same expression that of a point charge
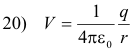
where r is equal to or greater than the radius of the sphere. At all points inside the sphere the electrical intensity is zero. As a consequence, the potential is the same at all internal points and is equal to the potential at its surface. Fig. 5 shows the graphs of the electric intensity E and potential V at points along a line through the center of a sphere of radius a and charge q.
Charge density, electric field intensity and electric potential on a charged
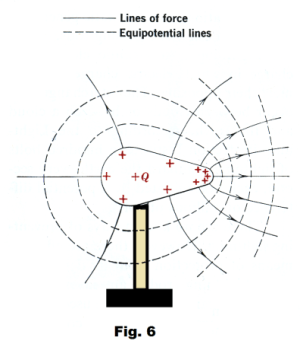
conductor. All of the excess charge on a charged conductor in which the charges are at rest (electrostatic situation) lies on its surface. The charge density and electric field intensity will in general vary from point to point on the surface with the highest charge density and highest electric field intensity occurring at points of greatest curvature. See Fig. 6. However, the electric potential does not vary from point to point on the surface. It is the same at all points on the surface. It is remarkable that the electric field intensity varies from point to point but the potential does not.
The electric field at the surface of a charged conductor is everywhere perpendicular to the surface. It is as a consequence of this fact that the potential is everywhere the same on the surface. There is no horizontal component to the electric field vector and so no work is done in moving a test charge on the surface.
The surface of a charged conductor is thus an equipotential surface. Furthermore, since the field within a charged conductor is zero, the entire interior of the conductor is an equipotential volume, at the same potential as the surface. Thus we can speak of the potential of a particular charged conductor since the potential everywhere on the conductor is the same.
References
1. Dull, Metcalfe, Brooks. Modern Physics.
2. Sears, Zemansky. University Physics
3. Semat, Katz. Physics.
4. Bennet. Physics.
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life