Electrostatics. Coulomb�s law. Coulomb. Electric field. Electric field intensity. Lines of force. Electric flux. Gauss� law. Dielectric strength.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Electrostatics. Coulomb’s law. Coulomb. Electric field. Electric field intensity. Lines of force. Electric flux. Gauss’ law. Dielectric strength.

Coulomb’s law. The force F between two point charges q and qʹ varies directly as the magnitude of each charge and inversely as the square of the distance between them.

where k is a constant of proportionality that depends on the system of units used. The force is directed along the line joining the two bodies and is repulsive if the bodies are of like charge and attractive if the forces are of unlike charge.

Coulomb’s law. MKS System of units. In the MKS system of units, F is in newtons, q and qʹ are in coulombs, and r is in meters. If the medium in which the charges are located is a vacuum,

k = 8.987×10⁹ nt m²/coul²

When the surrounding medium is not a vacuum, forces caused by charges induced in the medium reduce the resultant force between the charges.

If we define

Coulomb’s law becomes

where ε is the permittivity of the medium in which the charges are located. The permittivity ε of the medium is related to the dialectic constant K of the medium by

4) ε = K ε₀

where ε₀ is the permittivity of a vacuum. The value of ε₀ is 8.85×10^-12 coul²/nt-m², and for a vacuum, K = 1. For air, K = 1.00059, or nearly unity.

The dialectic constant of a medium is also termed its specific inductive capacity.

Def. Coulomb. The quantity of charge which in one second crosses a section of a conductor in which there is a constant current of one ampere.

Convenient submultiples of the coulomb:

1 μc = 1 microcoulomb = 10^-6 coulomb

1 μμc = 1 micromicrocoulomb = 10^-12 coulomb

The charge carried by an electron is

e = 1.602×10^-19 coulomb

Coulomb’s law. CGS Electrostatic System of units. In the CGS electrostatic system, F is in dynes, q and qʹ are in statcoulombs, r is in centimeters, and the constant k of Coulomb’s law is arbitrarily set equal to 1 (with the assumption that charges in a vacuum). In the CGS electrostatic system, Coulomb’s law is

for charges located in a vacuum. When the surrounding medium is not a vacuum, Coulomb’s law is

where K is the dialectic constant of the medium.

The unit of charge, the statcoulomb, also sometimes called an electrostatic unit (esu). The statcoulomb is defined implicitly by 5): when q = 1, q' =1, and r = 1, then F = 1.

Def. Statcoulomb. A charge of such magnitude that, when two such like charges are placed one centimeter apart in a vacuum, they will repel each other with a force of one dyne

The statcoulomb is widely used in the older literature of physics and engineering and is currently used in atomic and nuclear physics, but the MKS system is more practical and most used for other purposes.

Electric field. In general, a charged body exerts a force on any charge brought into the region surrounding it. The concept of an electric field represents a shift in point of view. Instead of viewing a charged body as exerting a force on a charge in its vicinity, we view the space itself as exerting a force on the charge. Thus an electric field is a region with a special property — the special property of being able to exert forces on charged bodies in it. We can envision an electric field through the device of lines of force (or flux lines). A line of force is the path that would be taken by a free unit positive charge if it were placed in the field. It is customary to think of them as emanating from positive charges and entering negative charges. It is a line so drawn that it is always tangent at any point to the electric field at that point. The magnitude at a given point is represented by the concentration of lines of force at that point.

Fig. 1(a) shows the electric field around an isolated positive charge and Fig. 1(b) shows the electric

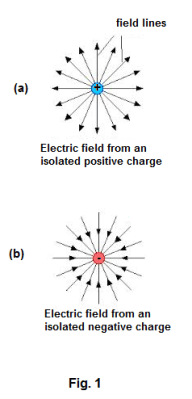
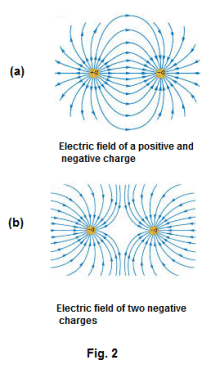
field around an isolated negative charge. Fig. 2(a) shows the electric field around two equal charges, one positive and one negative. Fig. 2(b) shows the electric field around two equal negative charges.

An electric field is an example of a force field. Other examples of force fields are magnetic fields and gravitational fields. A force field is a type of vector field. A vector field is a region of space in which a vector is associated with each point of the space. (An example of a vector field that is not a force field is the velocity at different points within a moving fluid.)

Def. Electric field. A region of space in which an electric force acts on any charge brought into it.

Def. Electric field intensity at a point in the field. The force that would be exerted on a unit positive charge if it were placed there.

In other words, if a small test charge q experiences a force F at a given point, the electric field intensity E at the point is given by

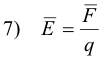
Thus electric field intensity at a point is force per unit charge at the point.

The magnitude of the electric field intensity E at a point P arising from a point charge q located a distance r away is thus

in the mks system and

in the cgs system.

Electric field intensity viewed as a flux density. Given a point P in some electric field R, let us pass a plane D through P perpendicular to the direction of the electric field intensity at point P. Then the electric field intensity at P can be alternatively viewed as a flux density at P. It can be viewed as so many lines of force per unit area (i.e. lines per sq. meter or per sq. centimeter) passing perpendicularly through plane D at point P. We thus have two ways of viewing electric field intensity. In many cases, the second way of looking at it is not only useful but necessary. To give some justification for this second point of view, consider the following:

MKS System. Let us arbitrarily assume that the number of lines of force emanating from a point charge q is q/ε. Under this assumption, the number of lines of force passing through a unit area on the surface of a sphere of radius r centered on the charge would be given by

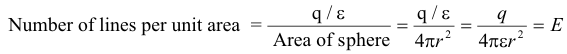
Thus, the number of lines per unit area on the sphere is equal to the electric field intensity E. In view of this observation, we make the agreement that the number of lines passing through a unit area perpendicular to the force field will be equal to the electric field intensity E.

CGS Electrostatic System. Let us arbitrarily assume that the number of lines of force emanating from a point charge q is 4πq/K where K is the dielectric constant. Under this assumption, the number of lines of force passing through a unit area of the surface of a sphere of radius r centered on the charge would be given by

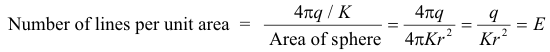
Thus, again in this case, the number of lines per unit area on the sphere would be equal to the electric field intensity E. Again, we make the agreement that the number of lines passing through a unit area perpendicular to the force field will be equal to the electric field intensity E.

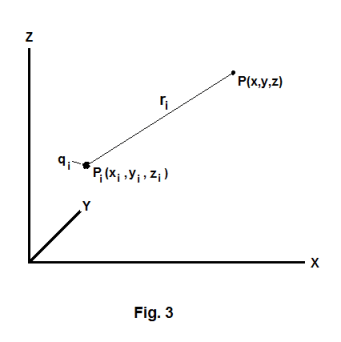
Electric field due to a collection of point charges. The electric field intensity at point P(x,y,z) arising from a charge q_i located at point P_i(x_i,y_i,z_i ) is

and r_i is the distance from P_i to P

See Fig. 3.

Now electric fields satisfy the superposition principle. This means that a probe charge placed at a point P in the neighborhood of a number of point charges q₁, q₂, q₃, ... will experience a force that is the vector sum of the forces produced by the individual charges. Thus, for n charges q₁, q₂, ..., q_n

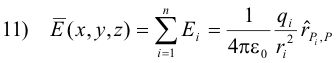
Electric field due to a continuous-charge distribution. When an electric field is established by a continuous distribution of charge rather than by a collection of point charges, we can compute the electric field intensity at a specified point P(x,y,z) by imagining the charge distribution to be divided up into small infinitesimal volume elements in which the entire charge of the element is considered to be concentrated at some point within the element, say its center. We can then apply equation 11) and use the methods of integral calculus. Taking the limit as the subdivisions become infinitesimally small we get

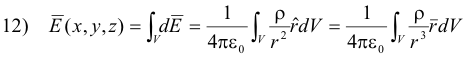
where ρ is the charge density (the amount of charge per unit volume), ε₀ is the permittivity of free space, dV is the differential volume element, is the vector from the differential volume element to point P, and r is the magnitude of .

Gauss’ law. Let E be an electric field existing over some region R of space and let S be a closed surface situated within R. Gauss’ law states (MKS system):

12) ∫∫_S E⋅dS = Σq/ε₀

where Σq is the algebraic sum of all positive and negative charges contained within surface S.

Physical interpretation of ∫∫_S E⋅dS .

∫∫_S E⋅dS = ∑ all electric flux (i.e. lines of force) leaving surface S - ∑ all electric flux entering surface S

Here a summation is performed over the surface S in which all flux leaving the surface is given a plus sign and all flux entering is given a negative sign. If ∫∫_S E⋅dS has a positive value, it means more flux is leaving the surface than is entering it and flux must be being created within the surface. If ∫∫_S E⋅dS has a negative value, it means more flux is entering the surface than is leaving it and flux must be being destroyed within the surface. If ∫∫_S V⋅dS = 0, it means no flux is being created or destroyed within S.

Thus, if outward flow is regarded as positive and inward flow is regarded as negative, the integral ∫∫_S E⋅dS can be said to represent the net outward flow of flux from the surface.

For more information see: Surface integral ∫∫_S V⋅dS representing a summation of flux passing through a closed surface.

In the CGS Electrostatic system, Gauss’ law is

12) ∫∫_S E⋅dS = 4πΣq

Gauss’ law can be used to easily deduce a number of important facts and formulas. We list some:

1. If the charges in a conductor are known to be at rest (i.e. if there is no current within the conductor --- the electrostatic case), then there can be no electric field within the conductor. Furthermore, if that conductor is charged, that charge must reside entirely on its surface. If a hole is made within the body of the conductor, the electric field within that hole must be zero.

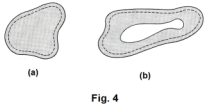
That there can be no electric field within the conductor is obvious since if there were a electric field, there would be a force on the free electrons and they would be moving (since free electrons move so freely within conductors). That the excess charge must reside on the surface of the conductor if it is charged can be shown using Gauss’ law. Fig. 4 (a) represents a solid conductor of irregular shape which has been given an excess charge q. Let us, in our imagination, conceive of a surface, called a Gaussian surface (shown dashed in the figure), located just inside the conductor surface. According to Gauss’ law the net electrical flux crossing this Gaussian surface in an outward direction equals the net positive charge enclosed by the surface. But if the charges are at rest, the electrical field at all points within the Gaussian surface is zero. Thus no flux crosses the Gaussian surface and the net charge within it must be zero. Consequently, all excess charge must lie outside this Gaussian surface and must, therefore, lie on the conductor surface. For a conductor that is hollow as shown in Fig. 4(b), the same is true (assuming there is no charge within the hollow).

The fact that the field within a closed conductor is zero is the basis for what is known as electrostatic shielding. One can demonstrate electrostatic shielding by placing a metal cap over the knob of an electroscope. If one brings a charged rod near an electroscope knob, there will be no divergence of the leaves if the knob is shielded by a metal cap. Electrical equipment is often placed within metal boxes to protect it from electric fields that may be present.

2. Electric field of a uniformly charged sphere. The field outside a uniformly charged sphere is the same as if all the charge were concentrated at the center of the sphere.

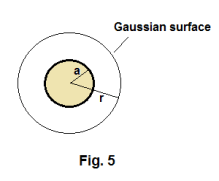
Consider the sphere of radius a shown in Fig. 5 which we assume to have a charge of q uniformly distributed throughout its volume. Let us imagine as a Gaussian surface a sphere of radius r constructed concentric with the sphere. From arguments involving symmetry we conclude that all the lines of force (flux) must be directed radially outward from the center of the sphere and that they are evenly spaced. Thus Gauss’ law ∫∫_S E⋅dS = Σq/ε₀ as applied to the Gaussian surface gives

13) ∫∫_S E⋅dS = q/ε₀

Since E is everywhere constant on the Gaussian surface and the area of the surface is 4πr², 13) becomes

14) 4πr²E = q/ε₀

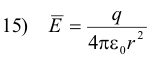
which is the same formula as the formula for the electric field of a point charge q.

This same result applies to a uniformly charged spherical shell or to any distribution of charge having spherical symmetry.

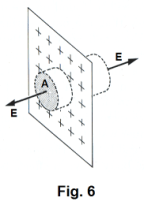
3. Electric field of an infinite plane sheet of charge. The electric field intensity at any point P outside a sheet of charge extending indefinitely in both directions with a uniform charge density σ is

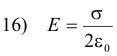
(σ is the charge per unit area of excess positive charge).

We derive the formula by constructing the Gaussian surface shown in dotted lines in Fig. 6, consisting of a cylinder whose walls are perpendicular to the sheet and whose ends have an area A. Due to the symmetry we reason that, because the sheet is infinite, the electric field intensity is the same on both sides of the sheet, that it is uniform, and that its direction is perpendicular to the sheet of the charge. We note that no flux lines cross the sides of the cylinder. Gauss’ law ∫∫_S E⋅dS = Σq/ε₀ as applied to the Gaussian surface then gives

2EA = σA/ε₀

E = σ/2 ε₀

4. Electric field of an infinite charged metal plate. The electric field intensity at any point P outside a charged metal plate extending indefinitely in both directions is

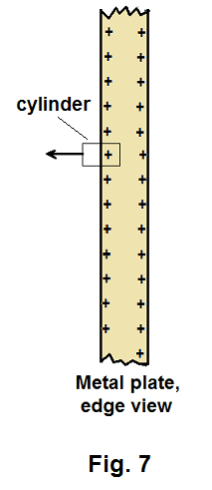
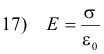
where σ is charge per unit area.

If such a metal plate is given a charge and the plate is of uniform thickness, the charge will spread out evenly on both surfaces. Let us construct a Gaussian surface consisting of the cylinder shown in Fig. 7. Its end faces are of area A and one face is inside and the other outside the plate. The electric field inside the plate is zero. The symmetry of the situation causes us to reason that the field will be perpendicular to the plate and directed outward if the charge is positive. Thus no flux will cross the walls of the cylinder. Applying Gauss’ law ∫∫_S E⋅dS = Σq/ε₀ to the Gaussian surface then gives

EA = σA/ε₀

E = σ/ε₀

5. Electric field between oppositely charged parallel plates. The electric field intensity at any point P between two oppositely charged parallel plates is

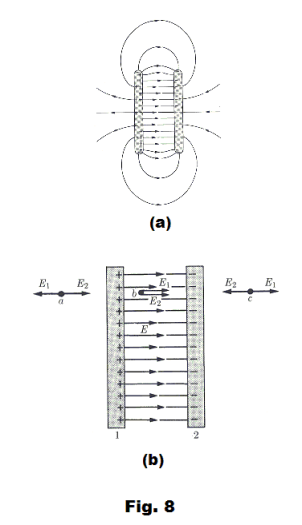
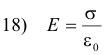
where σ is charge per unit area.

The electric field between two oppositely charged parallel plates is depicted in Fig. 8 (a). The field is essentially uniform between the plates with some spreading or “fringing” of the field around the edges. The fringing is often negligible and usually neglected. We will assume a uniform field between the plates and that the charges are evenly distributed over the plates.

The electric field intensity at any point can be considered to be the resultant of that due to two sheets of charge of opposite sign. At points a and c in Fig. 8 (b) the components E₁ and E₂ of sheets 1 and 2 are each of magnitude σ/2ε₀ [formula 16) above], but are oppositely directed, so their resultant is zero. At any point b between the plates the components are directed in the same direction and their resultant is σ/ε₀ .

6. Electric field just outside the surface of any charged conductor. The electric field immediately outside the surface of a charged conductor (in the electrostatic case — charges at rest) is everywhere perpendicular to the surface. The electric field intensity at any point P just outside the surface is

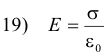
where σ is charge density (charge per unit area) at point P.

Let us construct a Gaussian surface consisting of the cylinder shown in Fig. 9 whose walls are normal to the conductor surface at the point of interest P. Its end faces are of area A and one face is inside and the other outside the conductor. We assume that the electric flux is perpendicular to the conductor surface at the point of interest P because if it were not there would be a component parallel to the surface that would cause movement of the free electrons and we are assuming all charges are at rest. Thus no flux passes through the cylinder walls. The electric field intensity at all points within the conductor is zero. Applying Gauss’ law ∫∫_S E⋅dS = Σq/ε₀ to the cylinder gives

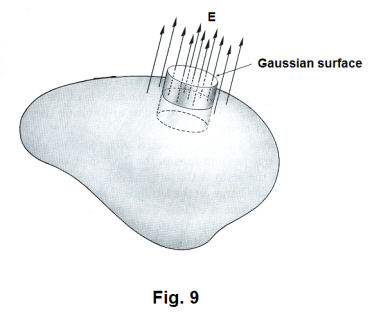
EA = σA/ε₀

E = σ/ε₀

Dielectric strength. For every dielectric there exists a certain limiting electric field intensity above which the substance loses its insulating properties and becomes conducting. The maximum electric field intensity that a dielectric can withstand without breakdown is called its dielectric strength. Air, for example, at atmospheric pressure, has a dielectric strength of about 3×10⁶ n/coul. Glass has a dielectric strength that is two or three times as great.

References

1. Dull, Metcalfe, Brooks. Modern Physics.

2. Sears, Zemansky. University Physics

3. Semat, Katz. Physics.

4. Bennet. Physics.