Polarization of light by crystal absorption, double refraction, reflection and scattering. Circular and elliptic polarization. Polaroid filters. Optical rotation.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

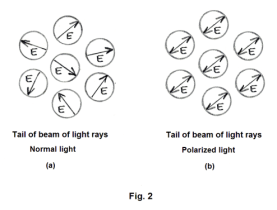
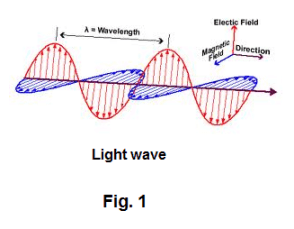
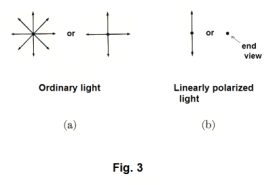
Polarization of light. A light wave can be envisioned as depicted in Fig. 1. Passing through the axis of the indicated direction of propagation are two planes perpendicular to each other, one shown in red corresponding to the direction of maximum electrical field and the other, shown in blue, corresponding to the direction of maximum magnetic field. We can envision a light beam as a collection of rays. Fig. 2(a) shows the tail ends of a collection of light rays traveling away from the reader. On the tail of each ray is shown the direction of the Electric field. As can be seen, the directions of the E field for the various rays are random. Fig. 2(b) shows the tail ends of a beam of polarized light. Here all the E fields are oriented in the same (or opposite) direction. A beam of light in which the direction of the E field is the same for all rays is said to be linearly polarized or plane polarized. The direction of the E field is referred to as the direction of vibration of a ray. Fig. 3 shows schematic diagrams conventionally used to denote ordinary light and polarized light.

There are different ways in which a beam of light can become polarized. We list some:

1. Passage through certain crystals.

2. Passage through a Polaroid filter.

3. Reflection from a surface.

4. Scattering by small particles or molecules (as in the atmosphere).

I Polarization by passage through crystals

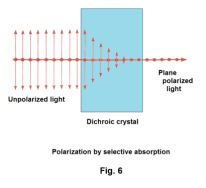
1. Polarization by crystal absorption. Some crystals, such as tourmaline, will absorb those vibrations that are perpendicular to the axis of the crystal and transmit those vibrations that are parallel to the axis. If a beam of light is sent through a thin plate of tourmaline, the transmitted beam will be linearly polarized in the direction parallel to the crystal axis. If this linearly polarized beam is then passed through a second tourmaline plate whose axis is at right angles to the axis of the first, no light will pass through the second crystal. If the second crystal is rotated so that its axis is parallel to the axis of the first crystal, the polarized beam will pass through the second crystal. At intermediate positions the intensity of the transmitted beam will be smaller than that transmitted when the axes are parallel.

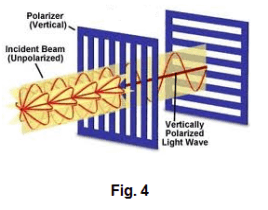
Polariscope. Two crystals of tourmaline used in the above way form the essence of a polariscope. The first crystal is called the polarizer. It serves the function of polarizing the light. The second crystal is called the analyzer. When the crystal axis of the analyzer is at right angles to that of the polarizer, no light passes through the analyzer. See Fig. 4. A polariscope can also be made from two sheets of Polaroid.

Malus’s law. Let the angle between the transmission axis of the polarizer and that of the analyzer be θ. Then the amount of light I transmitted through the analyzer depends on the value of θ as follows:

1) I = I_max cos² θ

where I_max is the maximum amount of light transmitted i.e. the amount transmitted at θ = 0. This law was discovered experimentally by Etienne Louis Malus in 1809.

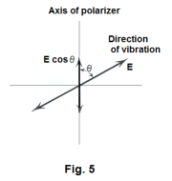
Derivation. When plane polarized light passes through a polarizer whose axis makes an angle θ with the direction of vibration, we can consider the vibrations of the light wave to have components parallel and perpendicular to the axis of the polarizer. See Fig. 5. If the amplitude of the polarized light is E, only the component parallel to the axis of the polarizer passes through it. This component has the amplitude E cos θ. The intensity I of a beam of light is proportional to the square of its amplitude. Thus I = αE² cos² θ. Since I = I_max when θ = 0, I_max = αE².

Substances such as tourmaline that have the property of absorbing vibrations in one direction much more strongly than in another are said to be dichroic. See Fig. 6.

2. Polarization by Double Refraction. Some transparent crystals, such as calcite and quartz, have the property that when one views an object through them one sees two images of the object. If one passes a narrow beam of light through them, the refracted beam is split into two parts which travel through the crystal and emerge as two separate beams. See Fig. 7(a). One of the beams obeys the ordinary laws of refraction and is called the ordinary ray. The other beam is called the extraordinary ray. The extraordinary ray does not always lie in the plane of incidence. Its speed, and consequently its index of refraction, depends on its direction of propagation through the crystal.

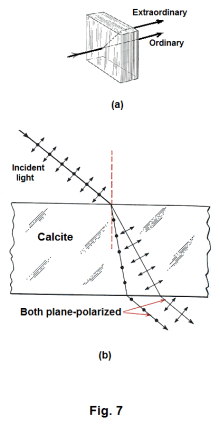
If one analyzes the two beams with a Polaroid analyzer one discovers that the two beams are both polarized, but that the directions of their vibrations are at right angles to each other. See Fig. 7(b).

If the arrangement of atoms in the calcite crystal is examined in a plane perpendicular to the optical axis, the atoms are found to be symmetrically distributed. If one examines them for any other plane, this is not the case. Both the optical and electrical properties are found to vary in different directions in the crystal.

Double refraction occurs in all crystals except those displaying cubic symmetry.

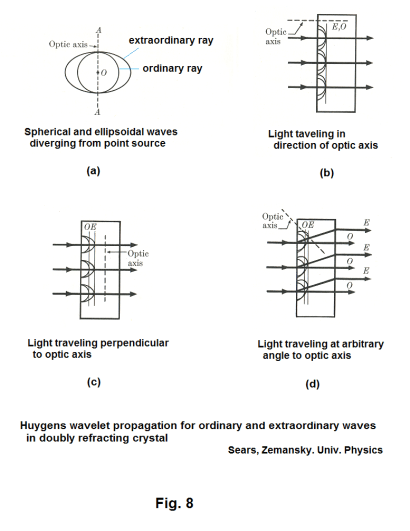
There is one particular direction in a doubly refracting crystal in which the ordinary ray and the extraordinary ray 1) do not separate and, in addition, 2) travel with the same speed. This particular direction in the crystal is known as the optic axis of the crystal. (The optic axis is a direction, not a line. All lines parallel to an optic axis are also optic axes.) There are also other directions in which the two rays do not separate, but in these cases, the two rays travel with different speeds. These directions that we speak of are those directions perpendicular to the optic axis. In Fig. 8(a) is shown the ordinary and extraordinary Huygens wavelets expanding from a point source within a doubly refracting crystal. (The diagram depicts a two dimensional slice of the spherical and ellipsoidal wavelets expanding in three dimensional space.) Fig. 8(b) shows the wave fronts for the ordinary and extraordinary rays when traveling in the direction of the optic axis. Note that the two rays travel at the same speed on the same path. Fig. 8(c) shows the wave fronts for the two rays when traveling perpendicular to the optic axis. Note that they travel the same path, but at different speeds. Fig. 8(d) shows the wave fronts for the two rays when traveling at an arbitrary angle to the optic axis. Note that in this case they travel different paths at different speeds.

Circular and elliptic polarization. Linearly polarized light represents a special and relatively simple type of polarization. When a crystal is cut with its faces parallel to the optic axis and a light beam is incident normally on its surface, the light will travel in a direction perpendicular to the optic axis. In this case, represented by Fig. 8(c), the ordinary and extraordinary rays will traverse the same path, but with different speeds. When the two rays emerge from the crystal, the ordinary and extraordinary rays are out of phase with each other and give rise to either elliptically polarized, circularly polarized, or linearly polarized light, depending on the phase difference as follows:

Phase difference is a multiple of π: Linearly polarized light

Phase difference is an odd multiple of π/2: Circularly polarized light

All other phase differences: Elliptically polarized light

The emerging rays will never interfere with each other. This is because their directions of polarization are perpendicular to each other. For two light waves to interfere, their vibrations must lie in the same plane.

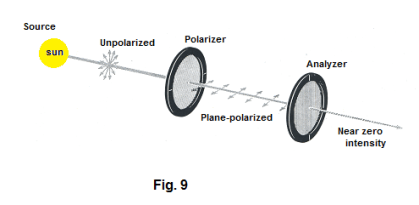
II Polarization by passage through a Polaroid filter. Polaroid film is commonly used to polarize light. One type of Polaroid film, patented by Edwin H. Land in 1929, consists of a thin layer of microscopic needle-like crystals of iodoquinine sulfate (herapathite) imbedded in a transparent nitrocellulose polymer film. The crystals are aligned during manufacture by stretching or applying electric or magnetic fields. With the needles aligned the film becomes dichroic. Improved Polaroid film has been developed in which polarizing molecules, rather than crystals, are imbedded in the film. Because it is cheap and can be produced in large quantities it has many applications.

III Polarization by reflection from a surface. Light reflected from a glass surface, a smooth body of water or a level highway is, in general, partially polarized. Let us consider the reflection of light from a glass plate as shown in Fig. 10. There is one particular angle of incidence for which the reflected ray is totally linearly polarized (shown as θ_P in the figure). This angle is called the polarizing angle. The direction of polarization in the reflected beam is that direction parallel to the surface of the plate (or, equivalently, that direction perpendicular to the plane of incidence, where the plane of incidence is that plane containing the incident beam and the normal at the point of incidence). At the polarizing angle, the reflected beam is totally reflected but of low intensity. For glass, only about 8% of the incident light is reflected. By using a bundle of thin glass plates, say seven or eight plates, the amount of light reflected can be increased to about 40% of the incident beam.

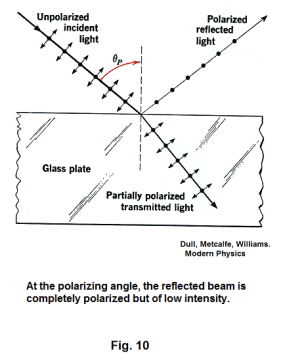
The polarizing angle corresponds to that angle of incidence at which the angle between the reflected ray and the refracted ray is 90^o.

An equation giving the value of θ_P is

1) tan θ_P = n₁/n₂

where n₁ is the index of refraction of the medium that the ray is traveling in before reflection and n₂ is the index of refraction of the reflecting material. This equation is known as Brewster’s law. Sir David Brewster discovered it experimentally in 1812.

IV Polarization by scattering. Light can be polarized by scattering from small particles or molecules. The blue light of the sky caused by scattering from particles or molecules whose diameter is on the order of magnitude of the wavelength of visible light is partially polarized. This can be confirmed by looking at the sky through a sheet of Polaroid. When one rotates the sheet, the intensity of the transmitted light changes and becomes a minimum when the axis of the sheet is at right angles to the direction of vibration of the light.

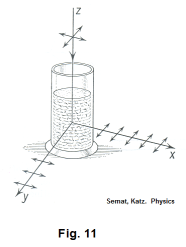
One can demonstrate polarization by scattering by sending unpolarized light down a tube of water containing fine particles in suspension. See Fig. 11. Light scattered in any horizontal direction is linearly polarized in the horizontal plane. Light scattered in the x direction has its vibrations in the y direction, light scattered in the y direction has its vibrations in the x direction .

Explanation. The direction of vibration of the incident light is in the horizontal plane. The varying electrical field of the incident light causes the electrons of the substance to vibrate in the horizontal plane. These electrons reradiate the energy absorbed from the incident light, so the direction of polarization of the scattered light must be horizontal.

Optical rotation. A number of substances including sugar, tartaric acid, and turpentine rotate the plane of polarized light. A water solution of sugar (sucrose) rotates the plane of polarization to the right. For a given path length, the angle of rotation is proportional to the concentration of the solution. Substances that rotate the plane of polarized light are said to be optically active. Instruments for measuring the angle of rotation are known as polarimeters.

References

Dull, Metcalfe, Brooks. Modern Physics

Sears, Zemansky. University Physics

Semat, Katz. Physics