Website owner: James Miller
Transverse and longitudinal wave propagation in an elastic medium. Sound. Intensity, loudness, pitch, frequency. Reflection, refraction, interference, beats. Infrasound, ultrasound. Doppler effect.

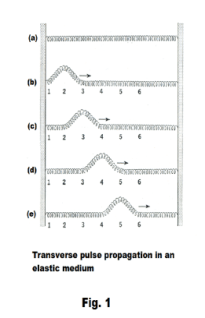
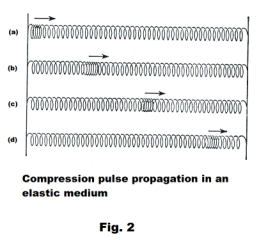
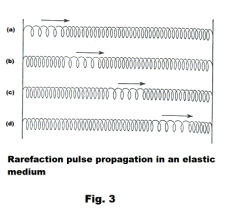
Propagation of pulses through an elastic medium. Let us stretch a long spiral spring between two supports several feet apart as shown in Fig. 1(a). If we hold the spring at point 3 and lift it at point 2 as shown in 1(b), and then release the spring, a transverse pulse will move from left to right as shown in 1(b) through 1(e). Let us now use a similar but larger diameter spring and pinch together several of the coils at the left end as shown in Fig. 2(a), and then release them. A compression pulse will move from the left side to the right side as shown in 2(a) through 2(d). Now let us, instead of pinching together several coils at the left end, stretch them apart as shown in Fig. 3(a), and then release them. A rarefaction pulse will then move from the left side to the right side as shown in 3(a) through 3(d). These three examples illustrate the propagation of pulses through an elastic medium (where the spring is the elastic medium). Note that in all cases a disturbance (a pulse) moves through the medium but the medium as a whole does not move (i.e. it is fastened at both ends and it only moves in the area of the pulse).
In the above, when we lift up, pinch together, or stretch apart several coils of the spring, we do work on the spring that is stored as potential energy. When we release the coils, this energy moves down the spring as a pulse, the energy passing from coil to coil in a manner similar to the way energy is transferred from billiard ball to billiard ball when we hit a billiard ball and it hits a second ball and it hits a third one, etc. Thus the movement of a pulse through a medium represents a movement of energy through the medium. As this energy moves through the medium, it distorts the medium in the locality of the pulse.
Def. Pulse. A single non-repeated disturbance that moves through a medium.
Model of an elastic medium. The particles of matter in an elastic medium act as if they were enmeshed in an elastic web. Each particle in the medium has some home position from which it may move a limited distance but is pulled back to its home position by an elastic force. Every particle in the medium is connected to its immediate neighbors by an elastic connection that is elastic both in regard to stretching and in regard to compression. When one particle is forced to move, it exerts forces on its immediate neighbors proportional to the displaced distance, pulling and pushing its neighbors. Metals, steel for example, are easily envisioned as elastic mediums. Other mediums are not so obviously elastic. However, stones and all solids as well as all liquids and gases are elastic. Proof of this is the fact that sound waves propagate through all substances, solid, liquid and gas, and they could not do this if the mediums were not elastic. The propagation of pulses or waves depends on the property of elasticity in the medium in order for it to work.
Def. Wave. A disturbance that moves through a medium. It may consist of a succession of pulses that move through a medium.
Note. The term wave often refers to a repeated disturbance pattern. It is also used to refer to a single instance of the pattern (as in the term “train of waves”).
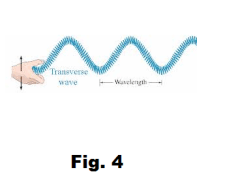
Def. Transverse wave. A wave in which the particles of the medium vibrate at right angles to the direction of propagation of the wave.
If we attach one end of a spiral spring to a support and whip the other end up and down as shown in Fig. 4, we can produce a series of pulses that move down the spring as a transverse wave. Water waves with their successive crests and troughs are an example of a transverse wave. As the waves advance, the water itself (the medium) rises and falls, but doesn’t move laterally.
Def. Longitudinal wave. A wave in which the particles of the medium vibrate to
and fro in the direction of propagation of the wave.
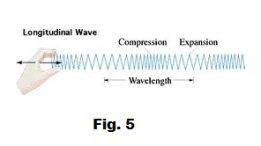
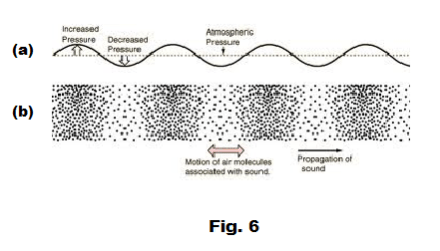
If we attach one end of a spiral spring to a support and vibrate the other end in a back-and-forth motion as shown in Fig. 5, we can cause a series of compression and rarefaction pulses to move down the spring as a longitudinal wave. Sound waves are longitudinal waves. They consist of a series of alternating compressions and rarefactions. See Fig. 6(b). Here the compressions and rarefactions represent changes in air density in the compression wave and also represent changes in air pressure. In Fig. 6(a) they are shown as deviations from atmospheric pressure. We see that a sound wave can be represented as a function of pressure versus time.
Def. Mechanical wave. A mechanical wave is a succession of pulses that moves through an elastic medium.
The waves we have just considered are mechanical waves. If we drop a stone into a still pool of water, circular waves will move out from where the stone hit the water. Water waves are mechanical waves. All matter (solid, liquid or gas) is elastic and meets the requirements for being an elastic medium. Mechanical waves are a disturbance moving through an elastic medium. In the example we have just given, the stone dropping into the water was the source of the disturbance and the waves are the disturbance. If a floating object such as a leaf were sitting in the water it would bob up and down as waves passed under it, but would not move substantially laterally. In water waves it may appear that the water moves laterally but, in fact, it only moves up and down. Sound waves are another important example of mechanical waves. An example of a type of wave that is not a mechanical wave, that stands in contradistinction to a mechanical wave, is an electromagnetic wave (such as a light wave) since electromagnetic waves travel in a vacuum and are not dependent on any known elastic medium for their propagation.
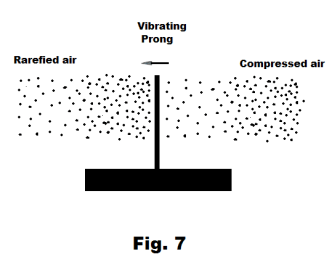
Source of sound -- a vibrating object. The source of a sound is, in general, a vibrating object or body. The source of the sound of a human voice is vibrating vocal cords, the source of the sound from a violin is the vibrating strings (amplified by a sound board), the source of the sound of a drum is the vibrating membranes. These vibrating objects create a train of compressions and rarefactions in the air in a way similar to that of a vibrating prong. See Fig. 7. As the prong swings it compresses the air on one side and creates a rarefaction on the other. Consider the ringing of a church bell. When the clapper hits the bell it vibrates, causing a ringing sound. When the sides of the bell vibrate, when they move in and out, they create compressions and expansions in the air next to the bell that are propagated out from the bell as a longitudinal wave. When the side of the bell moves outward, the particles of air next to it are pressed together and a compression is created. When it moves inward, a rarefaction is created. Because air is an elastic medium, these compressions and rarefactions move outward from the bell in a spherical mechanical wave in much the same way that water waves move out from a point where a stone has been dropped into a pool of water.
Def. Wavelength. The length of the disturbance corresponding to one complete vibration of the vibrator. For sound waves it is the length of one complete compression and rarefaction.
Def. Frequency. The number of vibrations per second of the vibrating body that produces the sound.
Def. Period. The time required for one complete vibration. T = 1/f where T= period and f = frequency.
Most sounds consist of a complex mix of waves of varying wavelengths. Most sounds do not consist of a uniform train of waves of equal lengths. Rather they consist of a complex mix of waves of varying wavelengths all superimposed on each other. The reason for this is that most vibrating bodies vibrate in a variety of ways, issuing not a single vibration, but a variety of vibrations. In addition, a vibrating body may vibrate in a regular way producing a train of waves of equal length or it may vibrate in an irregular way producing a train of waves of irregular length. If we strike a prong of a tuning fork with a rubber hammer it will vibrate in a regular way producing a train of waves of equal length. The various tones produced by musical instruments correspond to trains of waves of equal length. They are produced by vibrating objects that vibrate in a regular fashion. On the other hand if we knock two stones together, scrape our feet across the floor or drop a glass, we produce irregular vibrations consisting of trains of waves of irregular length. We produce noise, not music, and noise consists of irregular vibrations.
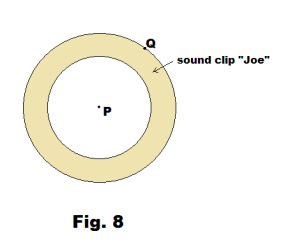
Propagation of a one-second sound clip. Let us consider the propagation of a one-second sound clip through air. Let us suppose the sound clip consists of the word “Joe”. Suppose someone located at some point P speaks the word “Joe”. As he utters the word “Joe” the density of the air molecules at point P varies in accordance with the compressions and rarefactions created by vibrations of his vocal cords. We could represent this sound clip by a graph of Δp v.s. time, where Δp is the deviation of pressure from atmospheric pressure. As the word “Joe” is uttered, the sound clip is propagated out from point P in a spherical wave. See Fig. 8. As it reaches and passes some distant point Q, an exact reproduction of the sound clip is played back at Q. Although we have used an example of sound propagation through air, it applies equally to sound propagation in any gas, liquid or solid i.e. in any elastic medium. It is not surprising that a disturbance in one part of an elastic medium would give rise to a disturbance in another part of the medium since all particles are connected. However, the fact that a disturbance in one part of a medium is replicated with great accuracy at a distant part of the medium is certainly interesting, remarkable and amazing.
How we hear. Vibrating bodies in our environment and the ability of air to transmit coded replicas of these vibrations is only part of the puzzle of sound. There is another piece of the puzzle. It is the miracle of the ear. Without the ear man and animal would live out their existence on earth in silence. The ear picks up the coded information from the air and translates it into electrical impulses understood by the brain. In the brain it becomes the sensory experience that we call sound. The ear consists of three parts (see Fig. 9):
(1) The outer ear. The outer ear consists of the familiar cup-like organ visible on the side of the head plus the tunnel-like auditory canal leading to the eardrum. The outer ear collects and amplifies sound waves and channels them in to the eardrum.
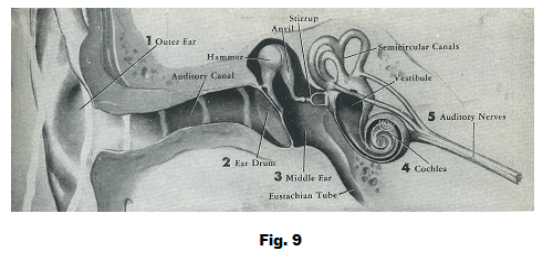
(2) The middle ear. The middle ear resembles a six-sided box and contains the eardrum and three bones, the hammer, anvil and stirrup. The hammer is attached to the eardrum and the stirrup is attached to a membrane of the inner ear called the oval window. The three bones act as levers transmitting vibrations from the eardrum to the inner ear, amplifying them in the process.
(3) The inner ear. The inner ear is a labyrinth of many intricate fluid-filled chambers and passageways. It has three connected parts: 1) the vestibule, 2) the semicircular canals, and 3) the cochlea. The vestibule is the central part of the inner ear. One side of it connects to the middle ear. The semicircular canals are three fluid-filled canals at right angles to each other, two vertical and one horizontal, that are important in giving a person his sense of balance (helping him maintain balance). The cochlea is a bony structure that is twisted like a snail-shell and contains three fluid-filled canals: the vestibular, tympanic, and cochlear canals. Along the inner wall of the cochlear canal is the organ of Corti which is about one and a quarter inches long and is the place where the amplified sound vibrations are converted to electrical impulses and sent to the brain via the auditory nerves. It contains 15,000 - 20,000 hair-like fibers (called hair cells) of varying lengths, some extending only a short distance into the cochlea, others extending to its apex (end). Different fibers are attuned to different frequencies, the frequencies a fiber responding to depending on its length. Those that respond to high frequencies are the shorter ones at the beginning of the spiral and those that respond to low frequencies are the longer ones that extend to the apex. Each hair cell is connected to its own auditory nerve receptor and when a hair cell responds to a vibration it sends an impulse to the brain.
By the time the sound waves reach the organ of Corti, their pressure amplitude is 22 times that of those impinging on the outer ear.
The vibration of air particles at the eardrum of a particular amplitude causes the eardrum to vibrate at a corresponding amplitude. The maximum pressure amplitudes in the loudest sounds that the ear can tolerate are of the order of magnitude of 280 dynes/cm2 (above and below atmospheric pressure of about 1,000,000 dynes/cm2). For a frequency of 1000 vibrations per second, this corresponds to displacement amplitudes of the air particles at the eardrum of about a thousandth of a centimeter. Thus the displacement amplitudes for even the loudest sounds is extremely small.
The maximum pressure amplitudes in the faintest sounds that the ear can hear at a frequency of 1000 vibrations per second are only about 2×10-4 dyne/cm2. This corresponds to displacement amplitudes of the air particles at the eardrum of about 10-9 cm. By way of comparison, the wavelength of yellow light is 6×10-5 cm and the diameter of a molecule is around 10-8 cm. It can thus be seen that the ear is an extremely sensitive organ.
The human ear is sensitive to sound in the frequency range of approximately 20 - 20,000 vibrations per second with considerable variation among people in regard to both the lowest and highest frequencies they can hear. Few people can hear sounds of less than 20 or more than 20,000 vibrations per second.
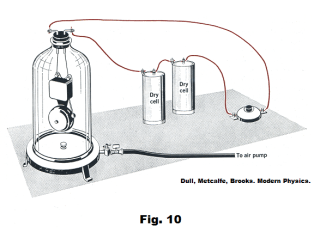
Sound propagation in various media. The following experiment demonstrates how the density of air affects the transmission of sound: Place an electric bell under a bell jar as shown in Fig. 10, connect the bell to some batteries, and start it ringing. While it is ringing, pump air out of the bell jar. As the air becomes less and less dense, the sound becomes fainter and fainter. If air is allowed to enter again, the sound becomes louder and louder. This demonstrates the important fact that sound will not travel in a vacuum. It must have a medium in which to propagate.
The air can carry many vibrations at the same time, and the vibrations can travel in many different directions. Yet each vibration travels as if it were the only one present. One can sit in a room and hear a friend talking, a bird singing, a fly buzzing, a dog barking, water running, and an airplane flying overhead all at the same time. With our brain working in conjunction with our two ears we recognize each sound, know its source, and know the approximate direction from which it comes.
Sound travels even better in water than in air. If you dive under water and strike together two rocks it is surprising how clearly you can hear them being hit together. The sound of an outboard motor far out on a lake can be heard quite plainly if you listen under water. In general, liquids are better transmitters of sound than air or other gases. And solids are better transmitters of sound than either liquids or gases. This is true because solids have a higher elastic modulus than liquids and liquids have a higher elastic modulus than gases. By listening to the rails one can hear a train coming from a great distance.
Speed of sound. The speed of sound in air at 0oC is 1087 ft/sec. As the temperature rises, the speed increases at a rate of approximately 2 ft/sec for each degree centigrade rise. The speed of sound in water is 4794 ft/sec and in steel it is 16,500 ft/sec.
Speed of a longitudinal wave. The speed v of a longitudinal wave depends on the elasticity and density of the medium:

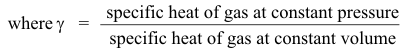
For monatomic gases (e.g. helium, neon, argon) γ = 1.67, and for air and diatomic gases (e.g. hydrogen, oxygen, nitrogen) γ = 1.40, approximately.
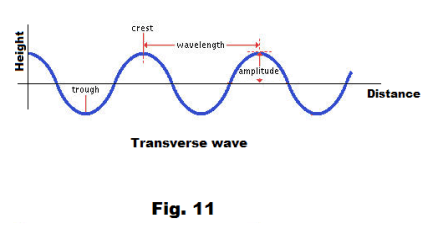
Anatomy of waves of regular wavelength. Fig. 11 shows a transverse wave of regular wavelength. The crests are those points at which the wave reaches its greatest displacement above the neutral position and the troughs are the points at which it reaches the greatest depth below the neutral position. The wavelength is the distance between two crests (or two troughs) and the amplitude is the amount of greatest displacement above the neutral position.
Fig. 12 shows the Pressure graph of a pressure wave associated with a sound wave of regular wavelength. The pressures are the pressures above and below atmospheric pressure. The pressure amplitude is the maximum amount by which the pressure differs from atmospheric pressure. The wavelength is the distance
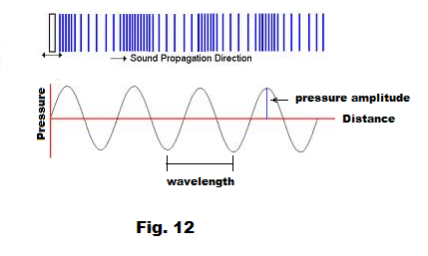
between any two corresponding points on the graph.
Intensity of a wave. The intensity of a wave is a measure of the amount of energy carried in the wave. The amount of energy carried in a wave is related to the amplitude of the wave. A high energy wave has a high amplitude and a low energy wave has a low amplitude. The greater the amplitude of the wave, the more energy is being carried by the wave. In water waves, large high waves carry a lot of energy and can do a lot of damage if they crash into a house on the beach. Small waves carry less energy and will do less damage.
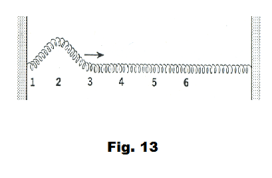
Consider the coiled spring stretched between two supports shown in Fig. 13. If we hold the spring at point 3 and raise it at point 2 and then release it, the pulse will travel down the spring. The higher we lift the spring at point 2, the more work we do on the spring, and the greater will be the amount of potential energy imparted to the spring. And the higher we lift it at point 2, the greater will be the amplitude of the pulse that moves down the spring. Greater potential energy imparted to the spring corresponds to greater pulse amplitudes.
The amount of energy E transported by a wave is directly proportional to the square of the amplitude A of the wave i.e.
E ∝ A2
Def. Intensity. The intensity of a sound wave measured at some observed point P is the rate of flow of energy (i.e. amount of energy passing per unit time, as ergs per sec) through a unit area perpendicular to the direction of propagation of the sound at P. Equivalently, it is the power flowing per unit area perpendicular to the direction of propagation at P. It can be expressed in ergs/sec per cm2 or in watts/cm2.
The intensity of the sound received from a particular source depends on the rate at which the source is emitting energy, the distance of the observer from the source, and the reflections that the sound waves undergo from such things as walls, ceilings, floor and objects in a room. Because sound emanates from a source in a spherical wave front and the area of the spherical front is directly proportional to the square of the distance from the source, it might be expected that the intensity of sound would diminish according to the square of the distance from the source. However, because of reflection and absorption, this is rarely the case.
The rate at which a source emits energy is increased by the amplitude and the area of the vibrating body.
It can be shown that the intensity I of a sound wave of regular wavelength is given by
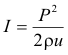
where P is the pressure amplitude, ρ is the average density of the air, and u is the velocity of the sound wave. It is also given by the formula
I = 2π2f2A2uρ
where f is the frequency in vibrations per second and A is the amplitude of vibration of the particles.
Loudness. The loudness of a sound is a physiological sensation that is dependent on the ear, subjective in nature, and difficult to measure. Sound intensity can be measured with acoustical apparatus, but loudness, because it is dependent on the human sense of hearing, cannot be measured by physical apparatus. Loudness is correlated with sound intensity in that a greater intensity produces a sensation of greater loudness, but the correlation is nothing like linear. It is more nearly logarithmic. A general rule of thumb is that the intensity must be increased by a factor of ten for a sound to seem twice as loud. The ear is not equally sensitive to sounds of different frequencies. As a consequence, a high frequency sound may not sound as loud as one of lower frequency having the same intensity. A measure of sound intensity has been devised that correlates somewhat directly with the sensation of loudness. It is called the intensity level of a sound and is given in decibels.
Def. Intensity level. The intensity level β of a sound, in decibels, is given by
Type of Sound |
Decibels |
Threshold of hearing |
0 |
Rustle of leaves |
10 |
Whisper |
10-20 |
Quiet office |
20-40 |
Automobile |
40-50 |
Conversation |
60-70 |
Heavy street traffic |
70-80 |
Elevated trains, Riveters |
90-100 |
Thunder |
110 |
Threshold of pain |
120 |
Table 1
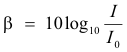
where I0 is an arbitrary reference intensity, taken as 10-16 watt/cm2. This value 10-16 watt/cm2 corresponds to the intensity of the faintest sound that can be heard, the threshold of hearing. We see from the formula that when I = I0, the value of β is 0. Thus a sound at the threshold of hearing has an intensity level of 0 decibels. Similarly, when I = 10 I0, β = 10, corresponding to an intensity level of 10 decibels; when I = 102 I0, β = 20, corresponding to an intensity level of 20 decibels; when I = 103 I0, β = 30, corresponding to an intensity level of 30 decibels; etc. Intensity levels for some common sounds are shown in Table 1. The smallest difference in loudness that the ear can distinguish is approximately 1 decibel.
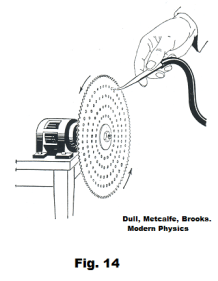
Pitch and frequency. The siren disc shown in Fig. 14 has five concentric rings of circular holes. The holes in the innermost ring (the first ring) are irregularly spaced while the holes in the outermost four rings (rings 2 - 5) are regularly spaced. The number of holes in rings 2 to 5 are 24, 30, 36, and 48 respectively. If we direct a stream of air at one of the rings while the disc is rotating rapidly, the air will vibrate because it is cut off regularly by the metal between the holes in the disc, and we will hear sound due to the vibrating air stream. If we direct the air stream at the innermost ring, the sound we hear will be an unpleasant, jarring one. It will be noise. Sounds produced by irregular vibrations are noise. If we direct the air stream against one of the four outermost rings we will hear a pleasant tone of constant pitch. It will be a musical tone. Sounds corresponding to regular vibrations are musical tones. If we direct the air stream at the 30 hole ring and the disc is rotating at a rate of 10 rpm, the pitch we hear will that corresponding to a frequency of 300 vibrations per second. If we increase the speed of the disc, the pitch will rise. If we slow the disc down, the pitch will drop. If we direct the stream of air against each of the rows 2 through 5 in succession, we will hear the notes do, mi, sol, do’. If we direct the air stream against the 24 hole ring and then at the 48 hole ring, the second sound will have a pitch that is an octave higher than the first (two tones are an octave apart if one has twice as many vibrations per second as the other).
The pitch of a sound depends on the frequency, but pitch is not the same as frequency. Pitch is related to frequency in much the same way that loudness is related to sound intensity. Pitch is a subjective physiological sensation depending on the ear while frequency is something that can be measured by physical apparatus.
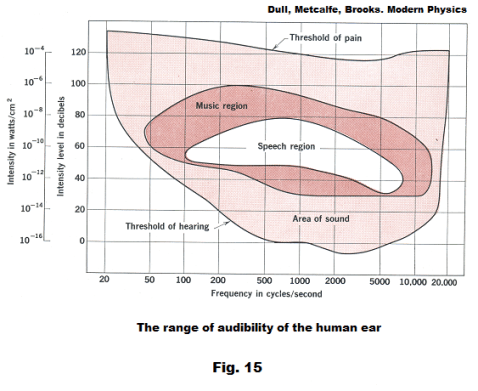
Range of audibility of the human ear. The range of human hearing extends from frequencies of around 20 to around 20,000 cycles per second. Fig. 15 shows the range of audibility of the human ear for different frequencies. The lower curve, the Threshold of hearing, represents the lowest intensity level at which sound waves of various frequencies can be heard. The upper curve, the Threshold of pain, is the intensity level above which a sound produces discomfort or pain.
Infrasound and ultrasound. Infrasound is sound below 20 cycles per second and ultrasound is sound above 20,000 cycles per second. Ultrasound has many uses because it can be focused in much the same way that light is focused with a searchlight. Ultrasonic waves are strongly reflected by obstacles. As a consequence, an ultrasonic device can detect objects by sending out a beam of ultrasonic waves and listening for reflected echos. The navy uses this type of device in the form of SONAR to detect submarines. Fishermen use such devices to detect schools of fish. Factories use them to detect flaws in metals, wood, and other materials. Other uses of ultrasound include medical imaging, dog whistles, controlling automatic garage doors, tenderizing frozen foods, nerve surgery, pasteurizing milk, sterilizing surgical instruments, and killing insects. Ultrasound can be produced in several ways. One way is by sirens. Another way is by applying a high frequency alternating voltage to the opposite faces of a quartz crystal, causing it to vibrate. Commonly used ultrasonic waves may have frequencies that range as high as 500 million vibrations per second. The M.I.T. Laboratory at Lexington, Mass., has produced sound waves that have a frequency of 70 billion vibrations per second.
The Doppler effect. A person standing by a railroad track will observe an abrupt drop in the pitch of a locomotive warning horn as the locomotive passes him. The frequency of the sound being emitted by the horn remains constant but the frequency heard by the observer is higher than the frequency being produced when the train is coming toward him and less than the frequency being produced when it is going away from him. This phenomenon in which the pitch that is heard is different from that being produced due to the movement of the source of the sound with respect to the observer is called the Doppler effect. To understand what occurs in the Doppler effect consider Fig. 16. The circles in the figures represent wave fronts of waves (i.e. leading edge of waves) emitted at times
t - 1∙T, t - 2∙T, t - 3∙T, t - 4∙T
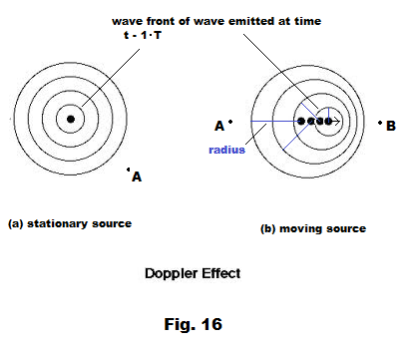
where t represents the current time and T is the period of the vibration. The innermost circle represents the wave front of the wave emitted at time t - 1∙T. In Fig. 16 (a) the source of the sound is stationary. The intervals between the wave fronts are uniform and equal. An observer at point A hears the same frequency as the frequency that was emitted. In Fig. 16 (b) the source is moving to the right with velocity v. The four black dots represent the centers of the four circles corresponding to the locations of the source at times
t - 1∙T, t - 2∙T, t - 3∙T, t - 4∙T
The blue lines are the radii of the circles. Because of this movement to the right, the wave fronts are closer together to the right of the source and further apart to the left of the source. As a consequence, an observer at A hears a frequency that is less than the one being produced and an observer at B hears a frequency that is greater than the one being produced.
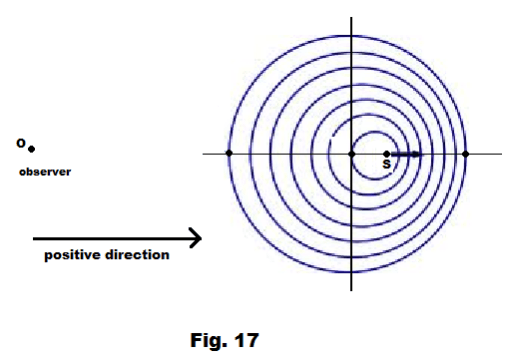
Let f be the emitted frequency, f' be the observed frequency, v be the velocity of sound, vo be the velocity of the observer and vs be the velocity of the source where vo and vs can be either positive or negative. Let the positive directions of vo and vs correspond to that of a vector extending from observer to source. See Fig. 17. Then
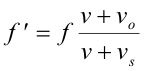
Reflection, refraction and absorption of sound. An example of sound reflection is the
familiar phenomenon of the echo. An echo is a repetition of a sound due to the reflection of the
sound wave from some surface. Sound will bounce off a hard surface (such as a cliff or side of a
building) in much the same way as a rubber ball will bounce off a wall.
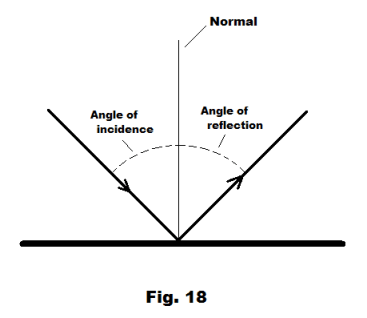
When a sound wave encounters an obstruction or a surface of discontinuity between media of different elastic properties, part of the wave is reflected back into the original medium and part is transmitted into the new medium with a different velocity and (except for the case of perpendicular incidence) a change in direction. Refraction is the bending of a wave as it passes across the boundary separating two different media. The laws that obtain for the reflection and refraction of sound are the same as those that obtain for the reflection and refraction of light. With reflection, the angle of incidence equals the angle of reflection. The angle of incidence is the angle between the incident ray and the normal and the angle of reflection is the angle between the reflected ray and the normal. See Fig. 18. The amount of sound that is reflected depends on the degree of dissimilarity between the two media. Sound waves traveling in air tend to bounce off hard, smooth surfaces and be absorbed by soft, rough surfaces.
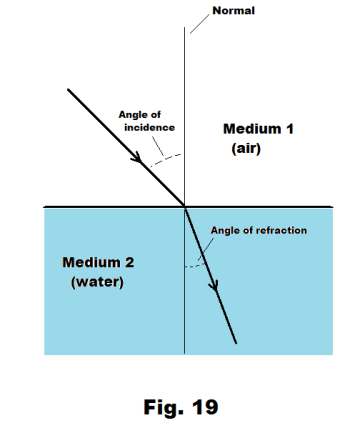
In the case of refraction, Snell’s law holds. Snell’s law states that when a wave passes across a medium boundary, going from Medium 1 into Medium 2, the angle of refraction is related to the angle of incidence by the formula
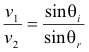
where v1 is the velocity of the wave in Medium 1, v2 is the velocity of the wave in Medium 2, θi is the angle of incidence, and θr is the angle of refraction. The angle of refraction is the angle between the refracted ray and the normal. See Fig. 19. In the special case where the ray strikes the surface perpendicularly (i.e. the angle of incidence is zero) there is no bending of the wave.
Def. Harmonic wave. A wave emitted by a source vibrating with simple harmonic motion. When plotted against time on a graph, it has the shape of a sine curve and is thus a sine wave. Because elastic materials, when disturbed, vibrate harmonically in accordance with Hooke’s law, harmonic waves are very common and sound waves are often naively envisioned as simple sine waves.
Mathematical representation of a harmonic wave. The mathematical representation of a harmonic wave moving in the positive x direction is
![]()
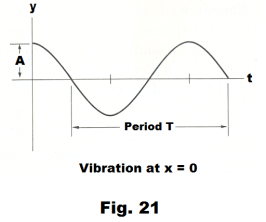
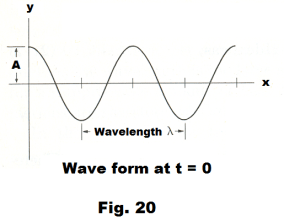
where A is the amplitude, T is the period, λ is the wavelength, t is time, y is displacement, x is distance from the source. Note that this is an equation in two variables: x and t. We can view it as a function of displacement v.s. x for some specified value of t or as a function of displacement v.s. t for some specified value of x i.e. either t or x can be regarded as a parameter. When t = 0, it has the form shown in Fig. 20. When x = 0, it has the form shown in Fig. 21.
Note. A harmonic wave can also be represented by
![]()
whose graph is simply the graph of 1) shifted to the right by π/2 with y = 0 at the initial condition x = 0, t = 0.
Harmonic waves and phase. In general a harmonic wave is represented by an equation of type
3) y = A sin (ωt + α)
where ω = 2π/T = 2πf, A is the amplitude, T is the period, and f is the frequency. The constant α has the effect of shifting the graph of
y = A sin ωt
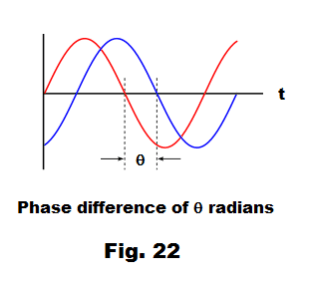
to the left by a fraction of a wavelength equal to α radians. Two harmonic waves
y1 = A sin (ωt + α)
and
y2 = A sin (ωt + β)
are said to have a phase difference of θ = β - α radians. See Fig. 22.
Principle of superposition of waves. The principle of superposition of waves states that when two or more waves pass through the same point, the total displacement at that point is equal to the sum (vector sum) of the displacements produced by the individual waves. This principle applies to all waves — transverse waves (as water waves or light waves), longitudinal waves (sound waves), etc.
Constructive and destructive interference. When two pulses meet at a point in space
their amplitudes are added. The pulses may enhance each other, giving a resultant pulse of greater
magnitude, or they may tend to cancel each other out, giving a resultant pulse of lesser magnitude,
depending on whether their amplitudes are of the same or opposite sign. If they enhance each
other, we have constructive interference at the point and if they tend to cancel each other out, we
have destructive interference at the point. Suppose the top two sine waves, (1) and (2), shown in
Fig. 23 represent sound waves of two
different frequencies passing through a
point. The bottom
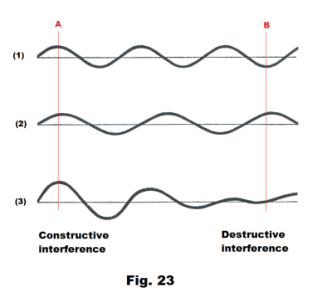
wave (3) is the resultant wave. We see that there is constructive interference at point A and destructive interference at point B.
Beats. When two tuning forks of different frequencies are sounded at the same time one hears a sound that is alternately louder and softer. The cause of this is the rapidly fluctuating constructive and destructive interference of the type shown in Fig. 23. This outburst of sound followed by comparative silence is called a beat. The number of beats produced per second is equal to the difference between the frequencies of the two vibrating bodies. If, for example, we sound tuning forks with frequencies of 252 and 256 at the same time, we will hear 4 beats per second.
References
Dull, Metcalfe, Brooks. Modern Physics
Sears, Zemansky. University Physics
Semat, Katz. Physics
World Book Encyclopedia
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life